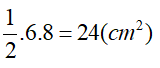• Tam giác ABC là hình gồm ba đoạn thẳng AB, BC, CA khi ba điểm A, B, C không thẳng hàng.
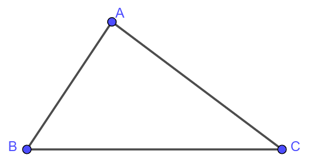
• Các trường hợp đặc biệt
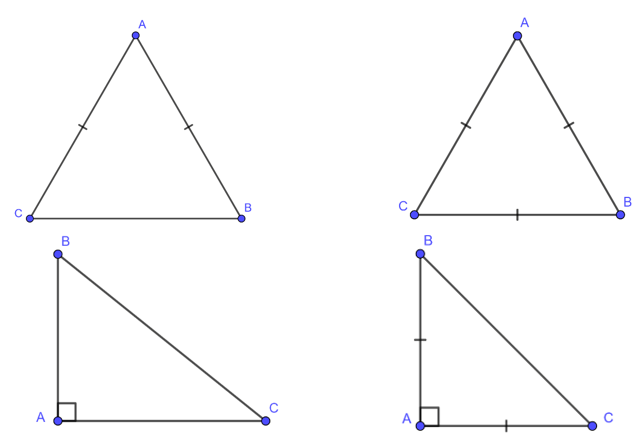
- Tam giác cân: là tam giác có hai cạnh bằng nhau.
- Tam giác đều: là tam giác có ba cạnh bằng nhau.
- Tam giác vuông: là tam giác có một góc vuông.
- Tam giác vuông cân: là tam giác vuông có hai cạnh góc vuông bằng nhau.
• Các đường thẳng đặc biệt trong tam giác:
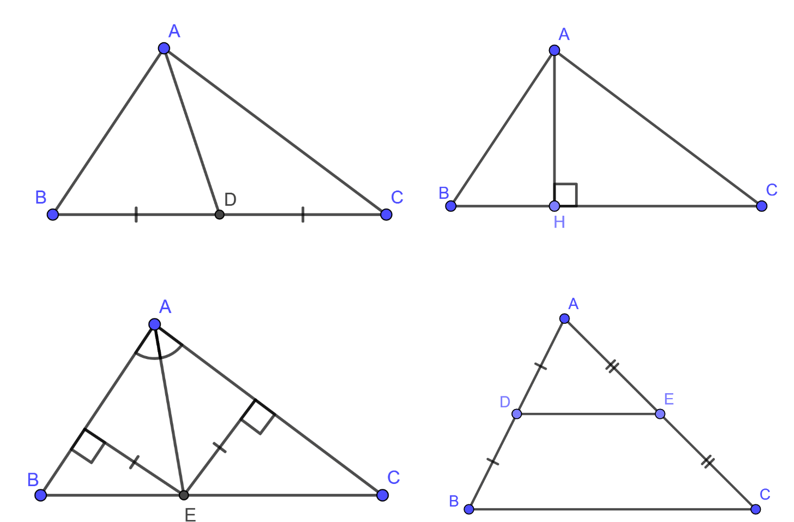
- Đường trung tuyến: Trong một tam giác đường thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện được gọi là đường trung tuyến của tam giác.
AD là đường trung tuyến của tam giác ABC.
- Đường cao: Đường thẳng đi qua một đỉnh và vuông góc với cạnh đối diện đỉnh đó được gọi là đường cao của tam giác.
AH là đường cao của tam giác ABC.
- Đường phân giác của một góc: là tập hợp các điểm nằm bên trong góc và cách đều hai cạnh của góc đó.
AE là đường phân giác của tam giác ABC.
- Đường trung bình: Đường trung bình của tam giác là đường thẳng đi qua trung điểm hai cạnh của tam giác.
DE là đường trung bình của tam giác ABC.
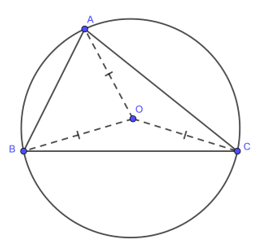
• Đường tròn ngoại tiếp tam giác: là đường tròn đi qua ba đỉnh của tam giác.
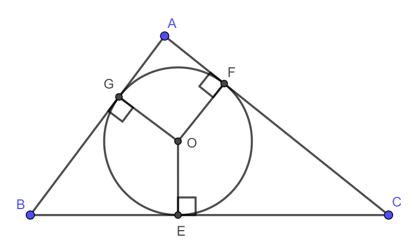
• Đường tròn nội tiếp tam giác: là đường tròn tiếp xúc với ba cạnh của tam giác.
• Chu vi tam giác: Chu vi tam giác bằng tổng độ dài ba cạnh của tam giác đó.
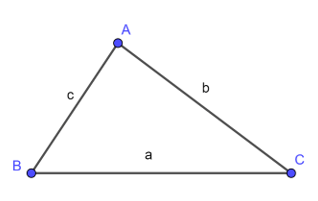
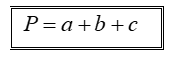
Trong đó, P là chu vi tam giác; a, b, c là độ dài ba cạnh của tam giác đó.
• Diện tích tam giác:
Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao ( cùng một đơn vị đo) rồi chia cho 2.
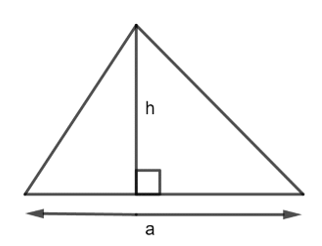
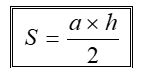
( S là diện tích, a là độ dài đáy, h là chiều cao)
Ví dụ : Cho tam giác ABC có độ dài ba cạnh là 6cm, 8cm, 10cm. Tính chu vi và diện tích tam giác ABC?Hướng dẫn:
Chu vi tam giác ABC là: 6 + 8 + 10 = 24(cm)
Ta có: + = 36 + 64 = 100 =Suy ra, tam giác ABC vuông với hai cạnh góc vuông là 6cm và 8cm
Vậy diện tích tam giác ABC là: