CHỦ ĐỀ 2: PHÉP TỊNH TIẾN VÀ PHÉP DỜI HÌNH

A. TÓM TẮT LÍ THUYẾT

1. ĐỊNH NGHĨA PHÉP TỊNH TIẾN

Định nghĩa: Phép tịnh tiến vectơ $\overrightarrow{v}$, kí hiệu $T\overrightarrow{v}$ là một phép dời hình biến điểm M thành M’ sao cho $M{M}'=\overrightarrow{v}$.

2. CÁC TÍNH CHẤT CỦA PHÉP TỊNH TIẾN

Định lí 1: Nếu phép tịnh tiến biến hai điểm M và N lần lượt thành hai điểm M’ và N’ thì M'N' =MN.

Ý nghĩa của định lí 1 là "Phép tịnh tiến không làm thay đổi khoảng cách giữa hai điểm bất kì".

Định lí 2: Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.

Hệ quả: Phép tịnh tiến biến:

  • Đường thẳng thành đường thẳng.
  • Tia thành tia.
  • Đoạn thẳng thành đoạn thẳng bằng nó.
  • Tam giác thành tam giác bằng nó.
  • Đường tròn thành đường tròn có cùng bán kính.
  • Góc thành góc bằng nó.

    • 3. BIỂU THỨC TOẠ ĐỘ CỦA PHÉP TỊNH TIẾN

    Trong mặt phẳng với hệ trục toạ độ Oxy, phép tịnh tiến theo vectơ $\overrightarrow{v}\left( a;b \right)$ biến điểm M(x; y) thành điểm M'(x’; y’) với:

    $\left\{\begin{matrix} x'=x+a & \\ y'=y+b & \end{matrix}\right.$

    4. ỨNG DỤNG CỦA PHÉP TỊNH TIẾN

    Bài toán 1: Cho hai điểm B và C cố định trên đường tròn (O, R) và một điểm A thay đổi trên đường tròn đó. Chứng minh rằng trực tâm tam giác ABC nằm trên một đường tròn cố định.

    Giải

    Nếu BC là đường kính thì trực tâm H của ∆ABC chính là A. Vậy H nằm trên đường tròn cố định (O, R).

    Nếu BC không phải là đường kính, vẽ đường kính BB' của đường tròn.

    Dễ thấy rằng nếu H là trực tâm của ∆ABC thì $\overline{AH}=\overline{{B}'C}$ .

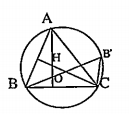
    Như vậy, phép tịnh tiến theo vectơ cố định $\overrightarrow{B'C}$ biến điểm A thành điểm H. Do đó, khi A thay đổi trên (O; R) thì trực tâm H luôn nằm trên đường tròn cố định là ảnh của đường tròn (O; R) qua phép tịnh tiến nói trên.

    Nhận xét: Như vậy, bài toán trên đã minh hoạ việc sử dụng phép tịnh tiến để tìm quỹ tích điểm. Và đó là một trong số những ứng dụng điển hình của phép tịnh tiến.

    Bài toán 2: Hai thôn nằm ở hai vị trí A và B cách nhau một con sông (xem rằng hai bờ sông là hai đường thẳng song song).

    Người ta dự định xây một chiếc cầu MN bắc qua sông (tất nhiên cần phải vuông góc với bờ sông) và đắp hai đoạn thẳng từ A đến M và từ B đến N. Hãy xác định vị trí của chiếc cầu MN sao cho AM + BN ngắn nhất.

    Giải

    Lấy điểm ${{M}_{0}}\in \left( a \right)$ ta có duy nhất điểm ${{N}_{0}}\in \left( b \right)$ sao cho ${{M}_{0}}{{N}_{0}}\bot \left( a \right)$ và ${{M}_{0}}{{N}_{0}}\bot \left( b \right)$

    Gọi ${B}'={{T}_{\overline{{{N}_{0}}{{M}_{0}}}}}$ và $M=A{B}'\cap \left( a \right)$, khi đó với điểm M’ bất kì thuộc (a) tương ứng với điểm N’ thuộc (b) (sao cho ${M}'{N}'\bot \left( a \right)$) ta có:

    Ta có:

    ${M}'A+{N}'B={M}'A+{M}'B\ge A{B}'=MA+M{B}'=MA+NB.$

    Tức là AM + BN ngắn nhất.

    Nhận xét: Như vậy, bài toán trên đã minh hoạ việc sử dụng phép tịnh tiến để thực hiện yêu cầu tối ưu (tìm điểm). Và đó cũng là một trong số những ứng dụng điển hình của phép tịnh tiến.

    5. PHÉP DỜI HÌNH

    Định nghĩa: Phép dời hình là một phép biến hình không làm thay đổi khoảng cách giữa hai điểm bất kỳ.

    Đinh lí: Phép dời hình biến:

  • Phép dời hình biến ba điểm thẳng hàng thành ba điểm thẳng hàng, ba điểm không thẳng hàng thành ba điểm không thẳng hàng.
  • Đường thẳng thành đường thẳng.
  • Tia thành tia.
  • Đoạn thẳng thành đoạn thẳng bằng nó.
  • Tam giác thành tam giác bằng nó.
  • Đường tròn thành đường tròn có cùng bán kính.
  • Góc thành góc bằng nó.