Vấn đề 5: DỰNG HÌNH
Phương pháp áp dụng
Ta thường thực hiện theo 4 bước đã biết.
Ví dụ l: (Bài 4/tr 6 – Sbt): Cho hai đường tròn không đồng tâm (O, R), (O1, R1) và điểm A trên (O, R). Xác định điểm M trên (O, R) và điểm N trên (O1, R1) sao cho $\overrightarrow{MN}=\overrightarrow{OA}$.
Giải
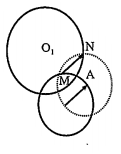
Phân tích: Giả sử đã dựng được hai điểm M, N thoả mãn điều kiện đầu bài, suy ra:
$N={{T}_{\overrightarrow{OA}}}\left( M \right)\Rightarrow N\in \left( A,R \right)={{T}_{\overrightarrow{OA}}}\left( \left( O,R \right) \right),$
tức N là giao điểm của hai đường tròn (A, R) và (O1, R1).
Cách dựng: Ta lần lượt thực hiện:
- Dựng (A, R).
- Xác định giao điểm N của (A, R) và (O1, R1).
- Dựng $\overrightarrow{MN}=\overrightarrow{OA}.$
Chứng minh: Theo cách đựng ta có ngay N thuộc (O1, R1) và:
MN//OA ⇒ OANM là hình bình hành ⇒ OM = AN = R ⇒ $M\in \left( O,R \right)$.
Biện luận: Bài toán có nghiệm hình phụ thuộc vào số giao điểm của hai đường tròn (A, R) và (O1, R1).
Ví dụ 2: Dựng hình thang ABCD (AB//CD) biết hai đường chéo AC = a, BD = b, góc ABC = α và đường trung bình MN = c.
Giải
.png)
Phân tích: Giả sử đã dựng được hình thang ABCD thoả mãn điều kiện đầu bài.
Thực hiện phép tịnh tiến:
${{T}_{\overrightarrow{CA}}}:D\mapsto {D}'$
khi đó tứ giác ACDD’ là hình bình hành nên ta có:
BD' = BA + AD' = AB + DC = 2MN = 2c
⇒ ∆BDD’ dựng được, (biết 3 cạnh).
Cách dựng: Ta lần lượt thực hiện:
Dựng ∆BDD’ với BD’ = 2c, BD = b, DD’ = a
- Dựng Dx // BD’
- Dựng By hợp với BD’ góc α, By cắt Dx tại C.
- Dựng Cz // DD’, Cz cắt BD" tại A
Thì tứ giác ABCD là hình thang cần dựng.
Chứng minh: Theo cách dựng ta có:
- CD//AB nên ABCD là hình thang; BD = b, góc ABC= α
- AC = DD' = a (do ACDD’ là hình bình hành) và:
$MN=\frac{1}{2}\left( AB+DC \right)=\frac{1}{2}\left( AB+A{D}' \right)=\frac{1}{2}B{D}'=c$
Biện luận: Bài toán có nghiệm hình:
.png)
