B. PHƯƠNG PHÁP GIẢI TOÁN
Vấn đề 1: TÌM VECTƠ TỊNH TIẾN $\overrightarrow{v}$ BIẾN HÌNH (H1 ) THÀNH HÌNH (H2)
Phương pháp áp dụng
Sử dụng định nghĩa và tính chất của phép tịnh tiến.
Chú ý: Chúng ta sẽ gặp một yêu cầu tương tự đối với phép dời hình.
Ví dụ 1: (Bài 2/tr 9 - Sgk): Cho hai đường thẳng song song (a) và (a'). Tìm tất cả các phép tịnh tiến biến (a) thành (a’).
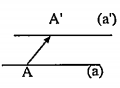
Giải
Mọi phép tịnh tiến T theo vectơ $\overrightarrow{v}=\overrightarrow{A{A}'}$ với $A\in \left( a \right)$ và ${A}'\in \left( {{a}'} \right)$ đều biến đường thẳng (a) thành (a’).
Nhận xét: Như vậy, với hai đường thẳng song song (a), (b) chúng ta có vô số các phép tịnh tiến biến (a) thành (b) và ngược lại. Các em học sinh hãy thực hiện thêm các yêu cầu sau:
a. Tìm các phép tịnh tiến biến đoạn thẳng AB thành đoạn thẳng CD, với ABCD là hình bình hành.
b. Cho bốn đường thẳng (a), (b), (a’), (b’) trong đó (a) cắt (b), (a) // (a’) và (b) // (b’). Tìm phép tịnh tiến biến (a) thành (a’) và biến (b) thành (b').
Ví dụ 2: Cho hai đường tròn (C1) và (C2) lần lượt có tâm O1, O2, và đều có bán kính R. Tìm phép tịnh tiến biến (C1) thành (C2).
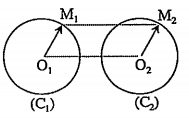
Giải
Lấy M1, tuỳ ý thuộc (C1) và gọi M2 là ảnh của M qua ${{T}_{\overline{{{O}_{1}}{{O}_{2}}}}}$, ta có:
$\overrightarrow{{{M}_{1}}{{M}_{2}}}=\overrightarrow{{{O}_{1}}{{O}_{2}}}\Leftrightarrow \overrightarrow{{{O}_{1}}{{M}_{1}}}=\overrightarrow{{{O}_{2}}{{M}_{2}}}$
$\Rightarrow {{O}_{2}}{{M}_{2}}=R\Leftrightarrow {{M}_{2}}\in \left( {{C}_{2}} \right)$
Ngược lại: lấy M2 là một điểm tùy ý thuộc (C2) và gọi M1 là tạo ảnh của nó qua ${{T}_{\overrightarrow{{{O}_{1}}{{O}_{2}}}}}$, ta có:
$\overrightarrow{{{M}_{1}}{{M}_{2}}}=\overrightarrow{{{O}_{1}}{{O}_{2}}}\Leftrightarrow \overrightarrow{{{O}_{1}}{{M}_{1}}}=\overrightarrow{{{O}_{2}}{{M}_{2}}}\Rightarrow {{O}_{1}}{{M}_{1}}=R\Leftrightarrow {{M}_{1}}\in \left( {{C}_{1}} \right)$
Vậy, ta thấy (C2) là ảnh của (C1) qua phép tịnh tiến ${{T}_{\overline{{{O}_{1}}{{O}_{2}}}}}$.
Nhận xét: Như vậy, với hai đường tròn phân biệt (C1), (C2) có cùng bán kính chúng ta có duy nhất phép tịnh tiến biến (C1) thành (C2) và ngược lại. Câu hỏi đặt ra là "Có bao nhiêu phép tịnh tiến biến đường tròn (C) thành chính nó ?"
Ví dụ 3: (Bài 12/tr 6 – Sbt): Cho hai tam giác bằng nhau ABC và A'B' C' (AB = A'B', BC = B’C’, CA = C’A’). Chứng minh rằng có không quá một phép dời hình biến ∆ABC thành ∆A'B' C'.
Giải
Giả sử tồn tại hai phép dời hình khác nhau F1, F2, cùng thoả mãn:
F1(∆ABC) = ∆A'B'C', F2(∆ABC) ≠ ∆A'B'C'.
Khi đó:
∃M: F1(M)=M1, F2(M) = M2, và M1 ≠ M2.
Vì F là phép dời hình nên:
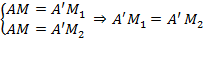
⇒ A’ thuộc đường trung của đoạn M1M2.
Tương tự, ta cũng thấy B’, C’ thuộc đường trung của đoạn M1M2, suy ra:
⇒ A’, B’, C’ thẳng hàng - mâu thuẫn.
Vậy, tồn tại duy nhất một phép dời hình biến ∆ABC thành ∆A'B'C'.
Nhận xét: Như vậy, để thực hiện ví dụ trên chúng ta đã sử dụng phương pháp phản chứng để giải, các em học sinh hãy ghi nhớ các bước khi sử dụng phương pháp này.
Ví dụ 4: (Bài 16/tr 7 – Sbt): Có hay không một phép dời hình F sao cho mọi đường thẳng đều biến thành đường thẳng song song với nó.
Giải
Giả sử tồn tại phép dời hình F thoả mãn điều kiện đầu bài. Khi đó, sẽ không tồn tại điểm M để F(M) = M vì nếu trái lại thì với đường thẳng (a) đi qua M ta có F(a) = (a’) và cả hai đường thẳng sẽ không thể song song bởi cùng đi qua điểm M.
Từ nhận xét trên với điểm A bất kì, giả sử:
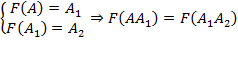
tức F biến đường thẳng (a) đi qua hai điểm phân biệt A, A1, thành đường thẳng (a’) đi qua hai điểm phân biệt A1, A2, và chúng cắt nhau tại A1, vô lí.
Vậy, không tồn tại phép dời hình thoả mãn điều kiện đầu bài.
Chú ý: Trong lời giải của ví dụ trên điểm mấu chốt là chứng minh nhận định "$\overline{\exists }$M:F(M) = M".
