Vấn đề 2: GIẢI BÀI TOÁN ĐỊNH TÍNH
Phương pháp áp dụng
Ta thường gặp các dạng yêu cầu sau:
Dạng 1: Chứng minh (H1) là ảnh của (H2) qua phép tịnh tiến vectơ $\overrightarrow{v}$, ta thực hiện theo các bước:
Bước 1: Lấy điểm M1, tuỳ ý thuộc (H1), ta đi chứng minh
${{M}_{2}}=T\overrightarrow{v}\left( {{M}_{1}} \right)\in \left( {{H}_{2}} \right).$
Bước 2: Ngược lại, lấy điểm M, tuỳ ý thuộc (H2), ta đi chứng minh ${{M}_{1}}=T\overrightarrow{v}\left( {{M}_{2}} \right)\in \left( {{H}_{1}} \right)$.
Dạng 2: Chứng minh tính chất K, ta thực hiện theo các bước:
Bước 1: Xác định một hoặc nhiều phép tịnh tiến để thiết lập mối liên kết giữa các yếu tố.
Bước 2: Sử dụng các tính chất của phép tịnh tiến để giải các yêu cầu của bài toán.
Chú ý: Chúng ta sẽ gặp một yêu cầu tương tự đối với phép dời hình.
Ví dụ 1: (Bài 3/tr 9 - Sgk): Cho phép tịnh tiến ${{T}_{\overrightarrow{u}}}$ theo $\overrightarrow{u}$ và phép tịnh tiến ${{T}_{\overrightarrow{v}}}$ theo $\overrightarrow{v}$.Với điểm M bất kì, ${{T}_{\overrightarrow{u}}}$ biến M thành điểm M’, ${{T}_{\overrightarrow{v}}}$ biến M' thành M". Chứng tỏ rằng phép biến hình biến điểm M thành M" là một phép tịnh tiến.
Giải
Đặt $\overrightarrow{a}=\overrightarrow{u}+\overrightarrow{v}$, ta có nhận xét:
$\overrightarrow{M{M}''}=\overrightarrow{M{M}'}+\overrightarrow{{M}'{M}''}=\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{a}$
Vậy, phép biến hình biến M thành M" là một phép tịnh tiến T theo vectơ $\overrightarrow{a}$.
Nhận xét: Trong ví dụ trên phép tịnh tiến ${{T}_{\overrightarrow{a}}}$ được gọi là tích (hoặc hợp thành) của hai phép tịnh tiến ${{T}_{\overrightarrow{u}}}$ và ${{T}_{\overrightarrow{v}}}$.Các em học sinh hãy thực hiện thêm các yêu cầu sau:
a. Chứng tỏ rằng tích của n phép tịnh tiến là một phép tịnh tiến.
b. (Bài 6/tr 6 – Sbt): Tìm các vectơ $\overrightarrow{u}$, $\overrightarrow{v}$ khác vectơ $\overrightarrow{0}$ để tích của hai phép tịnh tiến ${{T}_{\overrightarrow{u}}}$ và ${{T}_{\overrightarrow{v}}}$ là một phép đồng nhất.
c. Chứng tỏ rằng tích của hai hay nhiều phép dời hình là một phép dời hình.
Ví dụ 2: (Bài 15/tr7– Sbt): Chứng minh rằng phép dời hình F biến mỗi đường thẳng (a) thành đường thẳng (a’) vuông góc với (a) thì có một điểm duy nhất biến thành chính nó qua phép F.
Giải
Trước tiên, sẽ không tồn tại hai điểm phân biệt biến thành chính nó qua F bởi khi đó (a) sẽ trùng với (a’).
Gọi I là giao điểm của (a) với (a’), ta đi chứng minh F(I) =I.
Thật vậy, với A khác I giả sử:
$\left\{\begin{matrix} F\left ( A \right )=A_{1}\in\left ( a' \right)\\ F\left ( A_{1} \right )=A_{2}\\ F\left ( A_{3} \right )=A_{3} \end{matrix}\right.$ $\Rightarrow \left\{\begin{matrix} AA_{1}A_{2}A_{3} là hình vuông tâm I \\ F\left ( AA_{2} \right )=A_{1}A_{3} \end{matrix}\right.$ $\Rightarrow F\left ( I \right )=I$, đpcm.
Ví dụ 3: (Bài 9/tr 6-Sbt): Cho ba điểm A, B, C không thẳng hàng. Chứng tỏ rằng phép dời hình biến mỗi điểm A, B, C thành chính nó phải là phép đồng nhất.
Giải
Với phép dời hình F, thoả mãn:
F(A)= A, F(B) = B, F(C)=C.
Giả sử trái lại F không phải là phép đồng nhất, tức là:
$\exists M:F\left( M \right)={M}'$ và $M\ne {M}'$.
Vì F là phép dời hình nên:
⇒ A, B, C thuộc đường trung trực của đoạn MM'
⇒ A, B, C thẳng hàng - mâu thuẫn.
Vậy F phải là một phép đồng nhất.
Ví dụ 4: Giả sử phép dời hình f biến ∆ABC thành ∆A’B’C’. Chứng minh rằng:
a. Trọng tâm ∆ABC biến thành trọng tâm ∆A'BC’.
b. Trực tâm ∆ABC biến thành trực tâm ∆A'B'C'.
c. Tâm đường tròn ngoại tiếp (nội tiếp) ∆ABC biến thành tâm đường tròn ngoại tiếp (nội tiếp) ∆A'BC.
Giải
a. Gọi M là trung điểm của đoạn BC và G là trọng tâm ∆ABC. Giả sử:
f(M) = M' và f(G) =G’.
Từ tính chất không làm thay đổi khoảng cách giữa hai điểm, ta suy ra:
M là trung điểm của B’C’ ⇒ A'M' là trung tuyến. (1)
$\frac{2}{3}=\frac{AG}{AM}=\frac{{A}'{G}'}{{A}'{M}'}.$ (2)
Từ (1) và (2) suy ra G’ là trọng tâm ∆A'B’C’.
b. Gọi AA1, BB1 là hai đường cao của ∆ABC và H là trực tâm ∆ABC. Giả sử:
f(B1)=B1’, f(A1) = A’1, và f(H) =H’.
• Từ tính chất của phép dời hình, ta suy ra:
${H}'={{A}_{1}}{{{A}'}_{1}}\cap {{B}_{1}}{{B}_{1}}^{\prime }$ (3)
• Từ tính chất bảo toàn độ lớn góc của phép dời hình, ta suy ra:
${{A}_{1}}{{{A}'}_{1}},{{B}_{1}}{{{B}'}_{1}}$ là các đường cao của ∆A'B’C’. (4)
Từ (3) và (4) suy ra H’ là trực tâm ∆A'B'C'.
c. Ta lần lượt xét:
• Gọi O là tâm đường tròn ngoại tiếp ∆ABC. Giả sử:
$f\left( O \right)={O}'$.
Từ tính chất không làm thay đổi khoảng cách giữa hai điểm, ta suy ra:
O'A'= O'B'= O'C' bởi OA = OB = OC.
Vậy, điểm O là tâm đường tròn ngoại tiếp ∆A'B'C'.
• Gọi I là tâm đường tròn nội tiếp ∆ABC. Giả sử:
f(I) =I'.
Từ tính chất bảo toàn độ lớn góc của phép dời hình, ta suy ra:
$\widehat{{I}'{A}'{B}'}=\widehat{{I}'{A}'{C}'}\Rightarrow I$ thuộc đường phân giác của góc $\widehat{{{A}'}}$. (5)
$\widehat{{I}'{B}'{A}'}=\widehat{{I}'{B}'{C}'}\Rightarrow I$ thuộc đường phân giác của góc $\widehat{{{B}'}}$. (6)
Từ (5) và (6) suy ra I là tâm đường tròn nội tiếp ∆A'B'C.
Chú ý: Các ví dụ tiếp theo sẽ minh hoạ việc sử dụng phép tịnh tiến để chứng minh tính chất hình học của một hình phẳng.
Ví dụ 5: (Bài 5/tr 6 – Sbt): Cho tứ giác ABCD nội tiếp trong đường tròn (0, R), trong đó AD = R. Dựng các hình bình hành DABM và DACN. Chứng minh rằng tâm đường tròn ngoại tiếp tam giác DMN nằm trên (0, R).
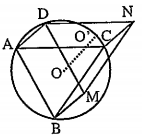
Giải
Từ giả thiết, ta có:
$\overrightarrow{AD}=\overrightarrow{BM}=\overrightarrow{CN}\Rightarrow {{T}_{\overrightarrow{AD}}}\left( \Delta ABC \right)=\Delta DMN$ suy ra ${{T}_{\overrightarrow{AD}}}\left( O \right)={O}'$ – là tâm đường tròn ngoại tiếp ∆DMN.
Mặt khác, ta cũng có:
$\overrightarrow{AD}=\overrightarrow{O{O}'}\Rightarrow O{O}'=R\Leftrightarrow {O}'\in \left( O,R \right)$, đpcm.
Ví dụ 6: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi:
\[MP+NQ=\frac{1}{2}\left( AB+BC+CD+DA \right)\]. (*)
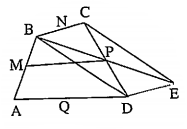
Giải
Thực hiện phép tịnh tiến ${{T}_{\overrightarrow{BC}}}:D\mapsto E$.
Khi đó tứ giác BCED là hình bình hành, vì P là trung điểm của CD nên P cũng là trung điểm của BE.
Do đó ta có:
$MP=\frac{1}{2}AE\le \frac{1}{2}\left( AD+DE \right)=\frac{1}{2}\left( AD+BC \right)$. (1)
Dấu bằng chỉ xảy ra ⇔ A, D, E thẳng hàng ⇔ AD∥BC
Chứng minh tương tự ta cũng có:
$NQ\le \frac{1}{2}\left( AB+CD \right).$ (2).
Dầu bằng chỉ xảy ra ⇔ AB∥CD
Cộng theo vế (1), (2), ta được:
$MP+NQ\le \frac{1}{2}\left( AB+BC+CD+DA \right).$ (3)
Vậy để có (*) thì dấu “=” xảy ra ở (3) ⇔ dấu “=” xảy ra tại (1) và (2)
⇔ ABCD là hình bình hành.
