Vấn đề 6: Hệ tọa độ đối với phép tịnh tiến

Vấn đề 6: HỆ TOẠ ĐỘ ĐỐI VỚI PHÉP TỊNH TIẾN

Phương pháp áp dụng

Ta trình bày phương pháp thực hiện hai dạng toán

Dạng 1: Xác định điểm M1 là ảnh của điểm ${{M}_{0}}\left( {{x}_{0}};{{y}_{0}} \right)$ qua phép tịnh tiến vectơ $\overrightarrow{v}\left( a;b \right)$.

Khi đó, toạ độ điểm M1(x; y) được cho bởi:

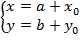
Dạng 2: Tìm phương trình của hình (H1) là ảnh của hình (H): f(x, y) = 0 qua phép tịnh tiến vectơ $\overrightarrow{v}\left( a;b \right)$.

Khi đó, mỗi điểm $M\left( x;y \right)\in \left( {{H}_{1}} \right)$là ảnh của một điểm ${{M}_{0}}\left( {{x}_{0}};{{y}_{0}} \right)\in \left( H \right)$qua phép tịnh tiến vectơ $\overrightarrow{v}\left( a;b \right)$, ta có:

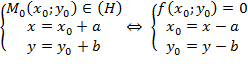
$\Rightarrow f\left( x-a,y-b \right)=0.$ (*)

Phương trình (*) chính là phương trình của (H1).

Chú ý: Với dạng toán 2 chúng ta còn có thể sử dụng tính chất đặc thù của phép tịnh tiến để giải, cụ thể:

a. Để tìm phương trình đường thẳng (d1) là ảnh của đường thẳng (d) qua phép tịnh tiến theo vectơ $\overrightarrow{v}$ chúng ta có thể thực hiện thêm theo các cách sau:

Cách 1: Thực hiện theo các bước:

Bước 1: Lấy hai điểm phân biệt A, B thuộc (d).

Bước 2: Sử dụng công thức xác định toạ độ của các điểm A1, B1, biết ${{A}_{1}}={{T}_{\overrightarrow{v}}}\left( A \right),{{B}_{1}}={{T}_{\overrightarrow{v}}}\left( B \right)$.

Bước 3: Viết phương trình đường thẳng (d1) đi qua hai điểm A1, B1.

Cách 2: Sử dụng tính chất (d1) song song với (d), ta thực hiện theo các bước:

Bước 1: Lấy điểm A thuộc (d).

Bước 2: Sử dụng công thức xác định toạ độ của điểm A1, biết ${{A}_{1}}={{T}_{\overrightarrow{v}}}\left( A \right)$.

Bước 3: Viết phương trình đường thẳng (d1) đi qua A1 và song song với (d).

b. Để tìm phương trình đường tròn (C1) là ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ $\overrightarrow{v}$ chúng ta có thể thực hiện theo cách sau:

Bước 1: Xác định toạ độ tâm I và bán kính R của (C).

Bước 2: Sử dụng công thức xác định toạ độ của điểm I1, biết ${{I}_{1}}={{T}_{v}}\left( I \right)$.

Bước 3: Viết phương trình đường tròn (C1) = (I, R).

Ví dụ 1: Trong mặt phẳng toạ độ Oxy, tìm toạ độ của điểm M1, là ảnh của điểm ${{M}_{0}}\left( 2;-1 \right)$ qua phép tịnh tiến vectơ $\overrightarrow{v}\left( 2;1 \right)$.

Giải

Giả sử ${{M}_{1}}\left( x;y \right)$, ta có:

$\overrightarrow{{{M}_{0}}{{M}_{1}}}=\overrightarrow{v}$ .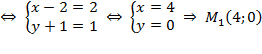

Vậy, ta được M1(4; 0).

Nhận xét: Như vậy, trong lời giải của ví dụ trên chúng ta đã sử dụng định nghĩa của phép tịnh tiến để tìm toạ độ điểm M1.

Ví dụ 2: Trong mặt phẳng toạ độ Oxy, tìm phương trình của đường thẳng (d1) là ảnh của đường thẳng (d) qua phép tịnh tiến vectơ $\overrightarrow{v}$, biết:

a. (d): x + 3y – 2 = 0 và $\overrightarrow{v}=\left( 1;1 \right)$.

b. $\left( d \right):2x+y-2009=0$ và $\overrightarrow{v}\left( 1;-2 \right)$.

Giải

a. Ta có ba cách trình bày sau:

Cách 1: Lấy điểm A(2; 0) ∈ (d) và gọi ${{A}_{1}}={{T}_{\overrightarrow{v}}}\left( A \right)$, ta có:

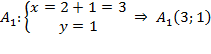Khi đó, phương trình đường thẳng (d1) được xác định bởi:

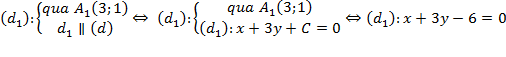Cách 2: Lấy hai điểm A(2; 0) và B(-1; 1) thuộc (d) và gọi:

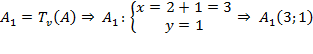
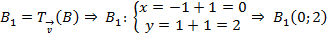
Khi đó, phương trình đường thẳng (d1) được xác định bởi:

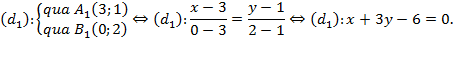
Cách 3: Mỗi điểm $M\left( x;y \right)\in \left( {{d}_{1}} \right)$ là ảnh của một điểm ${{M}_{0}}\left( {{x}_{0}};{{y}_{0}} \right)\in \left( d \right)$ qua phép tịnh tiến vectơ $\overrightarrow{v}\left( 1;1 \right)$, ta có:

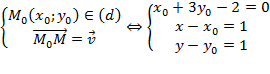
$\Rightarrow \left( x-1 \right)+3\left( y-1 \right)-2=0\Leftrightarrow x+3y-6=0$. (*)

Phương trình (*) chính là phương trình của (d1).

b. Nhận xét rằng đường thẳng (d) có vectơ chỉ phương (vtcp) là chính $\overrightarrow{v}\left( 1;-2 \right)$ nên phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến (d) thành chính nó.

Do đó, ảnh của (d) cũng có phương trình $2x+y-2009=0$.

Nhận xét: Như vậy, để thực hiện bài toán trên trong câu a:

- Ở cách 1, chúng ta đã sử dụng tính chất của phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

- Ở cách 2, chúng ta đã sử dụng điều kiện xác định một đường thẳng (cụ thể qua hai điểm phân biệt có duy nhất một đường thẳng).

- Ở cách 3, chúng ta đã sử dụng phương pháp quỹ tích.

Ví dụ 3: Trong mặt phẳng toạ độ Oxy, tìm phương trình của đường thẳng (d1) là ảnh của đường thẳng (d) qua phép tịnh tiến vectơ $\overrightarrow{v}$, biết:

a. $\left( d \right):4x-2y-2011=0$ và $\overrightarrow{v}\left( -1;-2 \right)$.

b. $\left( d \right):3x-4y+1=0$ và $\overrightarrow{v}$ có độ dài bằng $\sqrt{5}$ đồng thời có giá tạo với đường thẳng (d) một góc có sin bằng $\frac{2}{\sqrt{5}}$.

Giải

a. Nhận xét rằng đường thẳng (d) có vtcp $\overrightarrow{u}\left( 2;4 \right)$ cùng phương với $\overrightarrow{v}\left( -1;-2 \right)$ nên phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến (d) thành chính nó.

Do đó, ảnh của (d) cũng có phương trình $4x-2y-2011=0$.

b. Đường thẳng (d) đi qua điểm A(-1; 1), có vtcp $\overrightarrow{u}\left( 4;3 \right)$ và giả sử vectơ $\overrightarrow{v}\left( a;b \right)$, ta lần lượt có:

$\left| \overrightarrow{v} \right|=\sqrt{5}\Leftrightarrow \sqrt{{{a}^{2}}+{{b}^{2}}}=\sqrt{5}\Leftrightarrow {{a}^{2}}+{{b}^{2}}=5.$ (1)

$\sin \left( \left( d \right),{{g}_{\overrightarrow{v}}} \right)=\frac{2}{\sqrt{5}}\Leftrightarrow \sin \left( \overrightarrow{u},\overrightarrow{v} \right)=\frac{2}{\sqrt{5}}\Leftrightarrow \cos \left( \overrightarrow{u},\overrightarrow{v} \right)=\pm \sqrt{1-\frac{4}{5}}=\pm \frac{1}{\sqrt{5}}.$

Khi đó, ta lần lượt:

• Với $\cos \left( \overrightarrow{u},\overrightarrow{v} \right)=\frac{1}{\sqrt{5}}$, ta được:

$\frac{4a+3b}{\sqrt{{{4}^{2}}+{{3}^{2}}}.\sqrt{{{a}^{2}}+{{b}^{2}}}}=\frac{1}{\sqrt{5}}\overset{\left( 1 \right)}{\mathop{\Leftrightarrow }}\,\frac{4a+3b}{\sqrt{{{4}^{2}}+{{3}^{2}}}.\sqrt{5}}=\frac{1}{\sqrt{5}}\Leftrightarrow 4a+3b=5.$ (2)

Giải hệ tạo bởi (1) và (2), ta được a = 2 hoặc $a=-\frac{2}{5}.$

- Với a = 2 thì $b=-1$ nên $\overrightarrow{v}\left( 2;-1 \right)$, suy ra ${{T}_{\overrightarrow{v}}}\left( A \right)=\left\{ {{A}_{1}}\left( 1;0 \right) \right\}.$

Từ đó, suy ra:

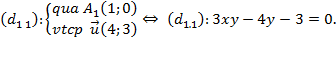
- Với $a=-\frac{2}{5}$ thì $b=\frac{11}{5}$ nên $\overrightarrow{v}\left( -\frac{2}{5};\frac{11}{5} \right)$, suy ra ${{T}_{\overrightarrow{v}}}\left( A \right)=\left\{ {{A}_{1}}\left( -\frac{7}{5};\frac{16}{5} \right) \right\}.$

Từ đó, suy ra:

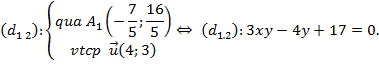
Với $\cos \left( \overrightarrow{u};\overrightarrow{v} \right)=-\frac{1}{\sqrt{5}}$ - Bạn đọc tự thực hiện.

Ví dụ 4: Trong mặt phẳng toạ độ Oxy, tìm phương trình của đường thẳng (d’) là ảnh của đường thẳng (d): x + 2y - 3 = 0 lần lượt qua các phép tịnh tiến theo các vectơ $\overrightarrow{v}$ và $\overrightarrow{u}$, biết:

a. $\overrightarrow{v}\left( 1;2 \right)$ và $\overrightarrow{u}\left( 2;-1 \right).$

b. $\overrightarrow{v}\left( 2;-1 \right)$ và $\overrightarrow{u}\left( 4;-2 \right).$

c. $\overrightarrow{v}\left( -2;-1 \right)$ và $\overrightarrow{u}\left( 2;-3 \right).$

Giải

a. Ta có thể trình bày theo các cách sau:

Cách 1: Đường thẳng (d) có vtcp $\overrightarrow{a}\left( 2;-1 \right)$ và đi qua điểm A(1; 1).

Ta có:

${{T}_{\overrightarrow{v}}}\left( A \right)={{A}_{1}}\left( 2;3 \right)$ và ${{T}_{\overrightarrow{u}}}\left( {{A}_{1}} \right)={A}'\left( 4;2 \right)$

Khi đó, phương trình đường thẳng (d') được xác định bởi:

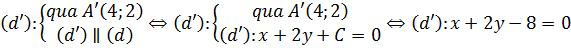
Cách 2: Đường thẳng (d) có vtcp $\overrightarrow{a}\left( 2;-1 \right)$ và đi qua điểm A(1; 1).

Ta có:

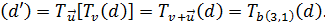
${{T}_{\overrightarrow{b}}}\left( A \right)={A}'\left( 4;2 \right).$

Khi đó, phương trình đường thẳng (d’) được xác định bởi:

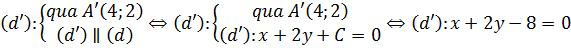
b. Nhận xét rằng đường thẳng (d) có vtcp $\overrightarrow{a}\left( 2;-1 \right)$ nên cùng phương với các vectơ $\overrightarrow{v}$ và $\overrightarrow{u}$. Suy ra, phép tịnh tiến theo các vectơ $\overrightarrow{v}$ và $\overrightarrow{u}$ biến (d) thành chính nó.

Do đó, ảnh của (d) cũng có phương trình x + 2y - 3 = 0.

c. Đường thẳng (d) có vtcp $\overrightarrow{a}\left( 2;-1 \right)$.

Ta có:

$\left( {{d}'} \right)={{T}_{u}}\left[ {{T}_{\overrightarrow{v}}}\left( d \right) \right]={{T}_{\overrightarrow{v}+\overrightarrow{u}}}\left( d \right)={{T}_{\overrightarrow{b}\left( 4;-2 \right)}}\left( d \right)$

tức đường thẳng (d) có vtcp $\overrightarrow{a}=\left( 2;-1 \right)$ cùng phương với $\overrightarrow{b}\left( 4;-2 \right)$ nên phép tịnh tiến theo các vectơ $\overrightarrow{v}$ và $\overrightarrow{u}$ biến (d) thành chính nó.

Do đó, ảnh của (d) cũng có phương trình x + 2y - 3 = 0.

Nhận xét: Như vậy, ví dụ trên đã minh hoạ phương pháp tìm phương trình đường thẳng (d’) là ảnh của đường thẳng (d) qua nhiều phép tịnh tiến. Và ở đó trong trường hợp không đặc biệt các em học sinh cần nắm vững các tính chất của phép tịnh tiến để từ đó đề xuất một lời giải ngắn gọn.

Ví dụ 5: Trong mặt phẳng toạ độ Oxy, tìm phương trình của đường tròn (C1) là ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ $\overrightarrow{v}$, biết:

a. $\left( C \right):{{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=4$ và $\overrightarrow{v}\left( 2;1 \right)$.

b. (Bài 7.b/tr 6-Sbt): (C): ${{x}^{2}}+{{y}^{2}}-4x+y-1=0$ và $\overrightarrow{v}\left( 1;-2 \right)$.

Giải

a. Ta có hai cách trình bày sau:

Cách 1: Đường tròn (C) có tâm I(-2; 1) và bán kính R = 2.

Gọi ${{I}_{1}}={{T}_{\overrightarrow{v}}}\left( I \right)$, ta có:

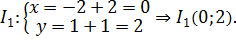
Khi đó, phương trình đường tròn (C) được xác định bởi:

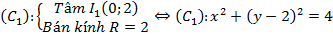
Cách 2: Mỗi điểm $M\left( x;y \right)\in \left( {{C}_{1}} \right)$ là ảnh của một điểm ${{M}_{0}}\left( {{x}_{0}};{{y}_{0}} \right)\in \left( C \right)$ qua phép tịnh tiến vectơ $\overrightarrow{v}\left( 2;1 \right)$, ta có:

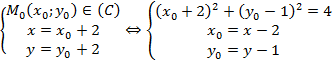
$\Rightarrow {{\left( x-2+2 \right)}^{2}}+{{\left( y-1-1 \right)}^{2}}=4\Leftrightarrow {{x}^{2}}+{{\left( y-2 \right)}^{2}}=4.$ (*)

Phương trình (*) chính là phương trình của (C1).

b. Ta có hai cách trình bày sau:

Cách 1: Mỗi điểm $M\left( x;y \right)\in \left( {{C}_{1}} \right)$ là ảnh của một điểm ${{M}_{0}}\left( {{x}_{0}};{{y}_{0}} \right)\in \left( C \right)$ qua phép tịnh tiến vectơ $\overrightarrow{v}\left( 1;-2 \right)$, ta có:

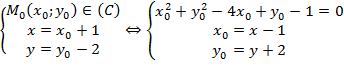
$\Rightarrow {{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}-4\left( x-1 \right)+y+2-1=0$

$\Leftrightarrow {{x}^{2}}+{{y}^{2}}-6x+5y+10=0$. (*)

Phương trình (*) chính là phương trình của (C1).

Cách 2: Đường tròn (C) có tâm $I\left( 2;-\frac{1}{2} \right)$ và bán kính $R=\frac{\sqrt{21}}{2}$.

Gọi ${{I}_{1}}={{T}_{\overrightarrow{v}}}\left( I \right)$, ta có:

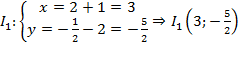Khi đó, phương trình đường tròn (C1) được xác định bởi:

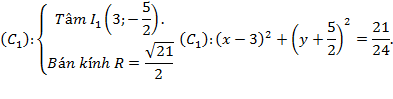
Ví dụ 6: (Bài 8/tr 6 – Sbt): Trong mặt phẳng toạ độ Oxy, cho hai đường thẳng (d) và (d') lần lượt có phương trình:

$Ax+By+C=0$ và $Ax+By+{C}'=0$.

Tìm những vectơ $\overrightarrow{v}\left( a;b \right)$ sao cho phép tịnh tiến T theo vectơ đó biến (d) thành (d').

Giải

Ta có thể trình bày theo các cách sau:

Cách 1: Với mỗi điểm $M\left( x;y \right)$ thuộc (d), ta có:

$Ax+By+C=0$. (*)

${{T}_{v}}\left( M \right)={M}'\left( x+a;y+b \right)\in \left( {{d}'} \right)\Rightarrow A\left( x+a \right)+B\left( y+b \right)+{C}'=0$

$\Leftrightarrow \left( Ax+By+C \right)+Aa+Bb-C+{C}'=0\overset{(*)}{\mathop{\Leftrightarrow }}\,Aa+Bb-C+{C}'=0.$ (**)

Vậy, các vectơ $\overrightarrow{v}\left( a;b \right)$ thoả mãn (**) sẽ thoả mãn điều kiện đầu bài.

Cách 2: Lấy các điểm tuỳ ý $M\left( x;y \right),{M}'\left( {x}';{y}' \right)$ theo thứ tự thuộc (d), (d’), ta có:

Ax + By + C = 0. (1)

Ax' + By' + C = 0. (2)

Từ đó, suy ra phép tịnh tiến theo vectơ:

$\overrightarrow{v}=\overrightarrow{M{M}'}\left( {x}'-x;{y}'-y \right)=\overrightarrow{M{M}'}\left( {x}'-x;-\frac{A\left( {x}'-x \right)-{C}'+C}{B} \right)$

sẽ thoả mãn điều kiện đầu bài.

Nhận xét: Như vậy, có vô số phép tịnh tiến biến đường thẳng (d) thành đường thẳng (d’) song song hoặc trùng với nó. Do đó, trong bài toán cụ thể với yêu cầu "Tìm một vectơ $\overrightarrow{v}\left( a;b \right)$ sao cho phép tịnh tiến T theo vectơ đó biến (d) thành (d')" các em học sinh chỉ cần lấy hai điểm M, M’ theo thứ tự thuộc các đường thẳng (d), (d') sẽ có ngay một vectơ $\overrightarrow{v}=\overrightarrow{M{M}'}$.

Ví dụ 7: (Bài 5/tr 9 - Sgk): Trong mặt phẳng toạ độ Oxy, với α, a, b là những số cho trước, xét phép biến hình F biến mỗi điểm M(x; y) thành điểm ${M}'\left( {x}';{y}' \right)$, trong đó:

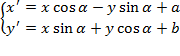
a. Cho hai điểm $M\left( {{x}_{1}};{{y}_{1}} \right),N\left( {{x}_{2}};{{y}_{2}} \right)$ và gọi ${M}',{N}'$ lần lượt là ảnh của M, N qua phép F. Hãy tìm toạ độ của M’ và N’.

b. Tính khoảng cách d giữa M và N, khoảng cách d’ giữa M’ và N’.

c. Phép F có phải là phép dời hình hay không ?

d. Khi α = 0, chứng tỏ rằng F là phép tịnh tiến.

Giải

a. Ta lần lượt có:

${M}'\left( {{x}_{1}}.\cos \alpha -{{y}_{1}}.\sin \alpha +a;{{x}_{1}}.\sin \alpha +{{y}_{1}}.\cos \alpha +b \right),$

${N}'\left( {{x}_{2}}.\cos \alpha -{{y}_{2}}.\sin \alpha +a;{{x}_{2}}.\sin \alpha +{{y}_{2}}.\cos \alpha +b \right).$

b. Ta lần lượt có:

$d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}.$ (1)