Vấn đề 4: TÌM TẬP HỢP ĐIỂM M
Phương pháp áp dụng
Ta thực hiện theo các bước:
Bước 1: Tìm một phép tịnh tiến $T\overrightarrow{v}$, biến điểm E di động thành điểm M.
Bước 2: Tìm tập hợp (H) của các điểm E.
Bước 3: Vậy tập hợp các điểm M là ảnh của (H) trong phép tịnh tiến $T\overrightarrow{v}$.
Ví dụ 1: (Bài 4/tr 9 - Sgk): Cho đường tròn (O) và hai điểm A và B. Một điểm M thay đổi trên đường tròn (O). Tìm quỹ tích điểm ${M}'$ sao cho $\overrightarrow{M{M}'}+\overrightarrow{MA}=\overrightarrow{MB}$.
Giải
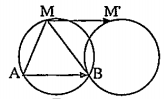
Từ giả thiết, ta có: $\overrightarrow{M{M}'}=\overrightarrow{MB}-\overrightarrow{MA}=\overrightarrow{AB}$
Tức là M' là ảnh của điểm ${M}$qua phép tịnh tiến theo vectơ $\overrightarrow{AB}$.
Vậy, quỹ tích điểm M’ là đường tròn (O’) là ảnh của đường tròn (O) qua phép tịnh tiến theo vectơ $\overrightarrow{AB}$.
Ví dụ 2: (Bài 3/tr 6 – Sbt): Cho đường tròn (O) với đường kính AB cố định, một đường kính MN thay đổi. Các đường thẳng AM và AN cắt tiếp tuyến tại B lần lượt tại P, Q. Tìm quỹ tích trực tâm các tam giác MPQ và NPQ.
Giải
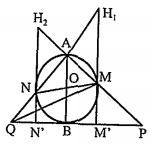
Ta lần lượt:
• Gọi .png) là trực tâm ∆MPQ, suy ra H chính là giao điểm của hai đường cao MM' và NQ (tức AQ). Ta có:
là trực tâm ∆MPQ, suy ra H chính là giao điểm của hai đường cao MM' và NQ (tức AQ). Ta có:
MM’ // AB ⇒ MH1 // OA
⇒ OA là đường trung bình của ∆MNH1
⇒ MH1 // 2OA $\Rightarrow \overrightarrow{M{{H}_{1}}}=\overrightarrow{AB}$
$\Rightarrow {{H}_{1}}={{T}_{\overrightarrow{AB}}}\left( N \right)$
Và vì M chạy trên (O) nên H1 chạy trên đường tròn $\left( {{O}_{1}} \right)={{T}_{\overrightarrow{AB}}}\left( \left( O \right) \right)$.
• Gọi .png) là trực tâm
là trực tâm .png) suy ra
suy ra .png) chính là giao điểm của hai đường cao NN' và MP (tức AP). Ta có:
chính là giao điểm của hai đường cao NN' và MP (tức AP). Ta có:
.png)
Và vì N chạy trên (O) nên .png) chạy trên đường tròn
chạy trên đường tròn .png)
Ví dụ 3: Cho hai đường tròn (O) và (O1) cắt nhau tại hai điểm, gọi A là một giao điểm. Đường thẳng (d) di động qua A và cắt hai đường tròn đã cho tại M và N. Trên hai tia AM và AN lấy hai điểm B và C sao cho $2\overrightarrow{BA}=2\overrightarrow{AC}=\overrightarrow{MN}$.Tìm quỹ tích các điểm B và C.
Giải
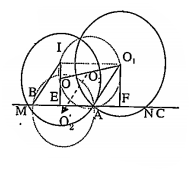
Dựng OE và .png) vuông góc với (d)
vuông góc với (d)
Ta có E, F lần lượt là trung điểm các đoạn AM, AN và:
$\overrightarrow{EF}=\frac{1}{2}\left( \overrightarrow{MA}+\overrightarrow{NA} \right)=\frac{1}{2}\overrightarrow{MN}=\overrightarrow{BA}=\overrightarrow{AC}$
Dựng .png) vuông góc với OE, khi đó tứ giác
vuông góc với OE, khi đó tứ giác .png) là hình chữ nhật
là hình chữ nhật
Từ đó suy ra:
$\overrightarrow{{{O}_{1}}I}=\overrightarrow{FE}=\overrightarrow{AB}\Rightarrow {{O}_{1}}ABI$ là hình bình hành
$\Rightarrow \overrightarrow{IB}=\overrightarrow{{{O}_{1}}A}\Rightarrow B={{T}_{\overrightarrow{{{O}_{1}}A}}}\left( I \right).$
Vì $\widehat{{O}'IO}$ vuông nên tập hợp các điểm I là đường tròn .png) đường kính
đường kính .png) , từ đó suy ra tập hợp các điểm B là đường tròn $\left( {{{{O}'}}_{2}} \right)$ với:
, từ đó suy ra tập hợp các điểm B là đường tròn $\left( {{{{O}'}}_{2}} \right)$ với:
$\left( {{{{O}'}}_{2}} \right)={{T}_{\overrightarrow{{{O}_{2}}A}}}\left[ \left( {{O}_{2}} \right) \right]$.
Tương tự ta có tập hợp điểm C là đường tròn .png) với:
với:
$\left( {{{{O}'}}_{3}} \right)={{T}_{\overrightarrow{OA}}}\left[ \left( {{O}_{2}} \right) \right].$
