Vấn đề 3: GIẢI BÀI TOÁN ĐỊNH LƯỢNG

Phương pháp áp dụng

Bằng việc thiết lập được các phép tịnh tiến thích hợp, ngoài việc chứng minh được các tính chất hình học ta còn có thể tính toán được các yếu tố trong một hình.

Ví dụ 1: (Bài 11/tr 6 – Sbt): Chứng minh rằng phép dời hình biến hai đường thẳng song song thành hai đường thẳng song song mà khoảng cách giữa hai đường thẳng song song đã cho bằng khoảng cách giữa các ảnh của chúng.

Giải

Với phép dời hình F và hai đường thẳng song song (a), (b), thoả mãn:

$F\left( a \right)=\left( {{a}'} \right)$ và $F\left( b \right)=\left( {{b}'} \right)$.

Gọi A, B theo thứ tự thuộc (a), (b) sao cho $AB\bot \left( a \right)$ và $AB\bot \left( b \right)$. (*)

Ta có:

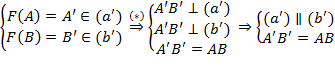, đpcm.

Ví dụ 2: Tứ giác ABCD có $AB=\sqrt{3},\,BC=3,\,CD=2\sqrt{3}$ và $\widehat{BAD}=\widehat{CDA}=60{}^\circ $. Tìm số đo các góc $\widehat{ABC}$ và $\widehat{BCD}$.

Giải

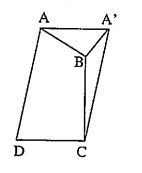
Xét phép tịnh tiến ${{T}_{\overrightarrow{DC}}}:A\mapsto {A}'$, khi đó tứ giác ADCA' là hình bình hành và $\widehat{BA{A}'}=60{}^\circ $.

Trong ∆ABA', ta có:

$\widehat{BA{A}'}=60{}^\circ $,

$A{A}'=2AB$.

Do đó, ∆ABA' vuông tại B và $\widehat{B{A}'A}=30{}^\circ $, ${A}'B=3$.

Vì ${A}'B=BC=3$ nên ∆BCA' cân tại B, do đó:

$\widehat{BC{A}'}=\widehat{B{A}'C}=\widehat{A{A}'C}-\widehat{B{A}'C}=60{}^\circ -30{}^\circ =90{}^\circ .$

$\widehat{BC{A}'}=360{}^\circ -\left( \widehat{BAD}+\widehat{CDA}+\widehat{BCD} \right)$

$=360{}^\circ -\left( 60{}^\circ +60{}^\circ +90{}^\circ \right)=150{}^\circ .$

Ví dụ 3: Từ đỉnh B của hình bình hành ABCD kẻ các đường cao BK và BH của nó. Biết rằng KH= a, BD=b. Tính khoảng cách từ B đến trực tâm E của ∆BHK theo a và b.

Giải – Bạn đọc tự vẽ hình

Ta có:

EH // KD (cùng vuông góc với BK)

EH // HD (cùng vuông góc với BH)

Do đó EHDK là hình bình hành, suy ra $\overrightarrow{EH}=\overrightarrow{KD}$

Thực hiện phép tịnh tiến vectơ $\overrightarrow{KD}$, ta có $K\mapsto D;E\mapsto H$, và $B\mapsto P$

Suy ra:

• Tứ giác BPDK là hình chữ nhật $\Rightarrow PK=BD=b$

• PH // BE mà BE ⊥ HK nên PH ⊥ HK

Xét tam giác vuông PHK, ta có:

$PH=\sqrt{P{{K}^{2}}-K{{H}^{2}}}=\sqrt{{{b}^{2}}-{{a}^{2}}}.$

Mà BE= PH nên $BE=\sqrt{{{b}^{2}}-{{a}^{2}}}.$