PHẦN II. QUANG HÌNH HỌC
CHƯƠNG VI. KHÚC XẠ ÁNH SÁNG
§26. KHÚC XẠ ÁNH SÁNG
A. TÓM TẮT LÝ THUYẾT
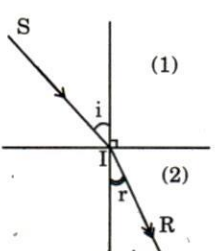
• Hiện tượng khúc xạ ánh sáng là hiện tượng tia sáng bị đổi phương đột ngột khi đi qua mặt phân cách giữa hai môi trường truyền ánh sáng. Mặt phân cách giữa hai môi trường gọi là mặt lưỡng phẳng hay lưỡng chất phẳng.
• Định luật khúc xạ ánh sáng:
* Tia khúc xạ nằm trong mặt phẳng tới
* Tia tới và tia khúc xạ nằm ở hai bên pháp tuyến tại điểm tới.
* Đối với hai môi trường trong suốt nhất định, tỉ số sin của góc tới và sin của góc khúc xạ là một hằng số. Hằng số này được gọi là chiết suất tương đối của môi trường khúc xạ đối với môi trường tới
$\large \frac{sini}{sinr}$ = n hay sin i = n sin r
- Nếu n > 1 ta bảo môi trường khúc xạ chiết quang hơn môi trường tới: Trong trường hợp này sin i > sin r ⇒ i > r (góc khúc xạ bao giờ cũng nhỏ hơn góc tới).
- Nếu n < 1 ta bảo môi trường khúc xạ chiết quang kém hơn môi trường tới. Trong trường hợp này sin i < sin r (góc khúc xạ bao giờ cũng lớn hơn góc tới)
• Chiết suất tỉ đối ( chiết suất tương đối). Trong công thức $\large \frac{sini}{sinr}$ = n, n được gọi là chiết suất tương đối của môi trường khúc xạ (môi trường (2)) đối với môi trường tới (môi trường (1))
n = $n_{21}$ = $\large \frac{n_{2}}{n_{1}}$ = $\large \frac{v_{1}}{v_{2}}$
• Chiết suất tuyệt đối của môi trường là chiết suất tương đối của môi trường đó với chân không;
$n_{1}$ = $\frac{c}{v_{1}}$; $n_{2}$ = $\frac{c}{v_{2}}$
B. CÂU HỎI VÀ BÀI TẬP
1. Thế nào là hiện tượng khúc xạ ánh sáng? Phát biểu định luật khúc xạ ánh sáng.
Giải
• Hiện tượng khúc xạ ánh sáng là hiện tượng tia sáng bị đổi phương truyền một cách đột ngột khi truyền qua mặt phân cách giữa hai môi trường truyền ánh sáng. Mặt phân cách giữa hai môi trường đó gọi là mặt lưỡng phẳng hay lưỡng chất phẳng.
• Định luật khúc xạ ánh sáng
* Tia khúc xạ nằm trrong mặt phẳng tới
* Tia tới và tia khúc xạ nằm ở hai bên pháp tuyến tại điểm tới.
* Đối với hai môi trường trong suốt nhất định, tỉ số sin của góc tới (sini) và sin của góc khúc xạ (sinr) là một hằng số. Hằng số này gọi là chiết suất tương đối của môi trường khúc xạ đối với môi trường tới
$\large \frac{sini}{sinr}$ = n hay sin i = n sin r
2. Chiết suất tỉ đối nai của môi trường (2) đối với môi trường (1) là gì?
Giải
Chiết suất tỉ đối của môi trường hai đối với môi trường một là tỉ số giữa sin góc tới (môi trường tới là môi trường (1)) và sin góc khúc xạ (môi trường khúc xạ là môi trường (2))
$n_{21}$ = $\large \frac{sini}{sinr}$
Hay chiết suất tương đối của môi trường hai đối với môi trường một là tỉ số giữa chiết suất tuyệt đối của môi trường (1) và môi trường (2)
$n_{21}$ = $\large \frac{n_{2}}{n_{1}}$
Hay chiết suất tương đối của môi trường (2) đối với môi trường (1) là tỉ số giữa vận tốc ánh sáng truyền trong môi trường (1) và vận tốc ánh sáng trong môi trường (2).
$n_{21}$ = $\large \frac{v_{1}}{v_{2}}$
3. Chiết suất (tuyệt đối) n của một môi trường là gì? Viết hệ thức liên hệ giữa chiết suất tỉ đối và chiết suất tuyệt đối.
Giải
Chiết suất tuyệt đối của một môi trường là chiết suất tương đối của môi trường đó đối với chân không.
- Công thức liên hệ giữa chiết suất tỉ đối (tương đối) và chiết suất tuyệt đối:
$n_{21}$ = $\large \frac{n_{2}}{n_{1}}$
• Chiết suất tuyệt đối của một môi trường là tỉ số giữa vận tốc ánh sáng trong chân không và vận tốc ánh sáng trong môi trường đó.
$n_{1}$ = $\large \frac{c}{v_{1}}$
4. Theo công thức của định luật khúc xạ ánh sáng, trường hợp nào không có hiện tượng khúc xạ?
Giải
Công thức của định luật khúc xạ ánh sáng cho ta :
$n_{21}$ = $\large \frac{sini}{sinr}$ = $\large \frac{n_{2}}{n_{1}}$ ⇒ $n_{1}$ sin i = $n_{2}$ sin r
Mà $n_{1}$, $n_{2}$ $\neq$ 0 khi i = 0 ⇒ sini = 0 ⇒ sinr = 0 ⇒ r = 0
Vậy nếu góc tới i = 0 khi góc khúc xạ r = 0 hay khi tia sáng tới vuông góc với mặt phân cách giữa hai môi trường (i = 0), tia ló sẽ truyền thẳng không bị gãy khúc nghĩa là không có tia khúc xạ.
5. Thế nào là tính thuận nghịch của sự truyền ánh sáng?
Chứng tỏ: $n_{12}$ = $\large \frac{1}{n_{21}}$. Nước có chiết suất là $\large \frac{4}{3}$. Chiết suất của không khí đối với nước là bao nhiêu?
Giải
Tính thuận nghịch của chiều truyền ánh sáng: Ánh sáng truyền đi theo đường nào, khi truyền ngược lại, ánh sáng cũng truyền theo đường đó.
Giả sử tia sáng truyền từ môi trường $n_{1}$ sang môi trường $n_{2}$, ta có:
$n_{1}sini_{1}$ = $n_{2}sinr_{1}$ ⇒ $\large \frac{sini_{1}}{sinr_{1}}$ = $\large \frac{n_{2}}{n_{1}}$ = $n_{21}$ (1)
Nếu tia sáng truyền ngược lại từ môi trường $n_{2}$ sang môi trường $n_{1}$, ta có:
$n_{2}sini_{2}$ = $n_{1}sinr_{2}$ mà $i_{2}$ = $r_{1}$ và $r_{2}$ = $i_{1}$ (tính thuận nghịch)
⇒ $n_{2}sinr_{1}$ = $n_{1}sini_{1}$ ⇒ $\large \frac{sinr_{1}}{sini_{1}}$ = $\large \frac{n_{1}}{n_{2}}$ = $n_{12}$ (2)
Từ (1) và (2) ⇒ $n_{21}$ = $\large \frac{1}{n_{12}}$
Nói chiết suất của nước là n = $\large \frac{4}{3}$ nghĩa là nói chiết suất tương đối của nước đối với không khí là n = $\large \frac{4}{3}$. Như vậy, chiết suất của không khí đối với nước là n' = $\large \frac{1}{n}$ = $\large \frac{3}{4}$
6. Một tia sáng truyền vào mặt thoáng của nước. Tia này cho một tia phản xạ ở mặt thoáng và một tia khúc xạ.
Người vẽ các tia sáng này quên ghi lại chiều truyền trong Hình 26.7.
Tia nào dưới đây là tia tới?
A.Tia $S_{1}I$
B. Tia $S_{2}I$
C. Tia $S_{3}I$
D. $S_{1}I$; $S_{2}I$; $S_{3}I$ đều có thể là tia tới.
.png)
Giải
Vì tia sáng tới vừa cho tia phản xạ, vừa cho tia khúc xạ ⇒ Chỉ có thể là: $S_{2}I$ là tia sáng tới, $IS_{1}$ là tia phản xạ và $IS_{3}$ là tia khúc xạ
⇒ Chọn câu B
7. Tia sáng truyền từ nước và khúc xạ ra không khí. Tia khúc xạ và tia phản xạ ở mặt nước vuông góc với nhau. Nước có chiết suất là $\large \frac{4}{3}$. Góc tới của tia sáng là bao nhiêu (tính tròn số)?
A. 37°
B. 42°.
C. 53°.
D. Một giá trị khác A, B, C.
Giải
.png)
Ta có tia khúc xạ vuông góc với tia phản xạ
⇒ i' + r = 90°
mà i' = i (định luật phản xạ ánh sáng)
⇒ i + r = 90° ⇒ sinr = cosi
Định luật khúc xạ ánh sáng cho ta
$\large \frac{4}{3}$sin i = sin r ⇔ $\large \frac{4}{3}$sin i = cos i
⇒ tgi = $\large \frac{3}{4}$ = 0, 75 ⇒ i $\approx$ 37°C
⇒ Chọn câu A
8. Có ba môi trường trong suốt 1, 2, 3. Với cùng góc tới I, một tia sáng khúc xạ khi truyền từ 1 vào 2 và từ 1 vào 3. Vẫn góc tới I, khi tia sáng truyền từ 2 vào 3 thì góc khúc xạ là bao nhiêu (tính tròn số)?
A. 22°
B. 31°.
C. 38°.
D. Không tính được.
.png)
Giải
Với cùng một góc tới i
• Khi truyền từ môi trường 1 vào môi trường 2 ta có:
.png)
• Khi truyền từ môi trường 1 vào môi trường 3, ta có:
.png)
.png)
• Khi truyền từ môi trường 2 vào môi trường 3, ta có
.png)
Với góc tới i chưa có giá trị cụ thể , nên ta chưa thể tìm được giá trị cụ thể của góc khúc xạ r
⇒ Chọn câu D
9. Một cái thước được cắm thẳng đứng vào bình nước có đáy phẳng, nằm ngang. Phần thước nhô khỏi mặt nước là 4 cm. Chếch ở trên có một ngọn đèn. Bóng của thước trên mặt nước dài 4 cm và ở đáy dài 8 cm. Tính chiều sâu của nước trong bình. Chiết suất của nước là $\large \frac{4}{3}$.
Giải
.png)
Phần thước nhô ra khỏi mặt nước và bóng của thước trên mặt nước là 4cm ⇒ Góc tới I của tia sáng đến mặt nước là 45°
Áp dụng định luật khúc xạ ánh sáng ta có :
sini = nsinr (chiết suất của không khí là n = 1)
.png)
.png)
Vậy mực nước trong bình sâu 6,4cm.
10. Một tia sáng được chiếu đến điểm giữa của mặt trên một khối lập phương trong suốt, chiết suất n = 1,50. Tìm góc tới i lớn nhất để tia khúc xạ vào trong khối còn gặp mặt đáy của khối.
.png)
Giải
.png)
Góc khúc xạ tối đa để tia khúc xạ còn gặp mặt đáy của hình lập phương phải đi qua đỉnh của hình lập phương. Như vậy trong trường hợp này, mặt phẳng tới sẽ là mặt phẳng chéo của hình lập phương (mặt phẳng chứa đường chéo của hình lập phương)
Gọi cạnh hình lập phương có độ dài a
Hình vẽ ta có:
.png)
.png)
Áp dụng định luật khúc xạ ánh sáng tại O
.png)
Vậy góc tới i lớn nhất là 60° để tia khúc xạ vẫn còn gặp mặt phẳng đáy.
