*Phương Trình bậc 2 hệ số thực
Ví dụ 1: Gọi ${{z}_{1}}$, ${{z}_{2}}$ là 2 nghiệm của phương trình ${{z}^{2}}+z+1=0$. Tính giá trị $P={{z}_{1}}^{2017}+{{z}_{2}}^{2017}$.
A. $P=1$. B. $P=-1$. C. $P=0$. D. $P=2$.
Hướng dẫn
Các em tính nghiệm rồi lưu vào X,Y
.png)
Thay vì tính mũ 2017 các em tính mũ 17 vì nó có cùng quy luật, do đó khoanh B.
*Phương trình bậc 2 hệ số phức
Câu 11: Trên tập số phức, gọi ${{z}_{1}},{{z}_{2}}$ là hai nghiệm của phương trình ${{z}^{2}}+2z+4i-2=0$ Tính giá trị
biểu thức $P=\frac{\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|}{4+\left| {{z}_{1}} \right|.\left| {{z}_{2}} \right|}$
A. $\frac{-\sqrt{10}+2\sqrt{2}}{2}$ B. $\frac{-\sqrt{10}+3\sqrt{2}}{2}$ C. $\frac{\sqrt{10}+3\sqrt{2}}{2}$ D. $\frac{-\sqrt{5}+3\sqrt{2}}{2}$
Hướng dẫn:
Tính $\Delta '$ rồi tính ra nghiệm : ${{z}_{1}}=1-i;{{z}_{1}}=-3+i$
Dùng nhanh biểu thức sau để tính căn :$\sqrt{\Delta }=\sqrt{\left| \Delta \right|}\angle \frac{agr(\Delta )}{2}$ rồi áp dụng công thức nghiệm phương trình bậc 2
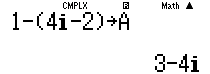

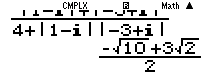
Vậy khoanh đáp án B
