Ví dụ 1: Kí hiệu ${{z}_{1}}$; ${{z}_{2}}$; ${{z}_{3}}$ là ba nghiệm của phương trình phức ${{z}^{3}}+2{{z}^{2}}+z-4=0.$ Tính giá trị của biểu thức $T=\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|+\left| {{z}_{3}} \right|.$

A. $T=4.$ B. $T=4+\sqrt{5}.$ C. $T=4\sqrt{5}.$ D.$T=5.$

Hướng dẫn

Các em vào giải phương trình bậc 3

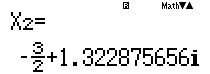
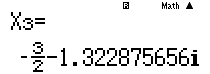
Để lưu nghiệm $X2$ vào X các em bấm hiện như thế này là được

Sau đó lưu nghiệm $X3$ vào Y sau đó phải vào hệ CMPLX không được sang hệ COMPL không là mất phần ảo

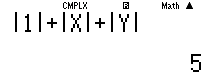
3.Một số dạng khác

Ví dụ 1: [Chuyên Biên Hòa – Hà Nam]Cho ba số phức ${{z}_{1}},{{z}_{2}},{{z}_{3}}$ thoả mãn điều kiện $\left| {{z}_{1}} \right|=\left| {{z}_{2}} \right|=\left| {{z}_{3}} \right|=1$ và ${{z}_{1}}+{{z}_{2}}+{{z}_{3}}=0$ . Tính $A={{z}_{1}}^{2}+{{z}_{2}}^{2}+{{z}_{3}}^{2}$

A.1 B.0 C. -1 D. $1+i$

Hướng dẫn

Chọn : ${{z}_{1}}=\frac{1}{2}+\frac{\sqrt{3}}{2}i,{{z}_{2}}=\frac{1}{2}-\frac{\sqrt{3}}{2}i,{{z}_{3}}=-1$

Bấm máy ta được:

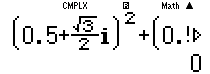
Ví dụ 2: Cho các số phức z thỏa mãn $\left| z \right|=5$. Biết rằng tâp hợp các điểm biểu diễn của các số phức $w=(3+4i)z-3i$ là một đường tròn. Tính bán kính r của đường tròn đó.

A. $r=\sqrt{5}.$ B. $r=5.$ C. $r=\sqrt{10}.$ D. $r=25.$

Hướng dẫn:

Các em biến đổi đơn giản như sau: $w=(3+4i)z-3i\Leftrightarrow w+3i=(3+4i)z$ lấy module 2 vế ta được : $\left| w+3i \right|=\left| 3+4i \right|\left| z \right|=25$ vậy tập hợp biểu diễn $w$ là đường tròn tâm $(0;-3)$ và bán kính là 25

Ví dụ 3: Nếu số phức thoả mãn $\left| z \right|=3$ thì phần thực của $\frac{1}{3-z}$ bằng:

A. $\frac{1}{3}$ B. $\frac{1}{6}$ C. 6 D. 3

Hướng dẫn

Ở đây bài toán đúng với mọi số thoả mãn $\left| z \right|=3$ nên các em chỉ cần chọn một số $z$ bất kì thỏa mãn là được chúng ta chọn là $3i$

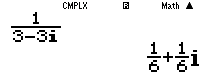
Vậy khoanh đáp án B