Ví dụ 1. Tính tích phân $I=\int\limits_{1}^{2}{2x\sqrt{{{x}^{2}}-1}\text{d}x}$ bằng cách đặt $u={{x}^{2}}-1,$ mệnh đề nào dưới đây đúng ?
A.$I=2\int\limits_{0}^{3}{\sqrt{u}\text{d}u}.$ B.$I=\int\limits_{1}^{2}{\sqrt{u}\text{d}u}.$ C.$I=\int\limits_{0}^{3}{\sqrt{u}\text{d}u}.$ D.$I=\frac{1}{2}\int\limits_{1}^{2}{\sqrt{u}\text{d}u}.$
Hướng dẫn
Tính tích phân rồi so với giá trị ở các đáp án
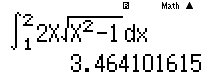
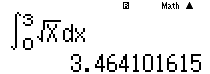
Ví dụ 2: Biết $\int\limits_{0}^{1}{\frac{3x-1}{{{x}^{2}}+6x+9}dx}=3\ln \frac{a}{b}-\frac{5}{6}$ trong đó a,b nguyên dương và $\frac{a}{b}$ là phân số tối giản. Hãy tính $ab$
A.$ab=-5$ B.$ab=\frac{5}{4}$ C.$ab=12$ D.$ab=6$
Hướng dẫn:
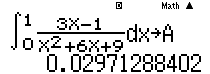
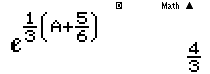

Ví dụ 3: Giả sử $\int\limits_{3}^{5}{\frac{\text{d}x}{{{x}^{2}}-x}}=a\ln 5+b\ln 3+c\ln 2.$ Tính giá trị biểu thức $S=-2a+b+3{{c}^{2}}$.
A. $S=-2$. B. $S=3$. C. $S=0$. D. $S=6$.
Hướng dẫn:
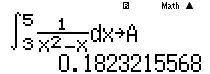
$A=a\ln 5+b\ln 3+c\ln 2\to {{e}^{A}}={{5}^{a}}{{.3}^{b}}{{.2}^{c}}$

${{5}^{a}}{{.3}^{b}}{{.2}^{c}}=\frac{6}{5}={{2.3.5}^{-1}}\to a=-1,b=c=1$ Vậy khoanh D
