CHƯƠNG II - ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
§1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
A. TÓM TẮT LÍ THUYẾT
Môn hình học không gian là môn học nghiên cứu các tính chất của các hình nằm trong không gian.
Hình học không gian có các đối tượng cơ bản là "điểm", "đường thẳng " và "mặt phẳng".
1. QUAN HỆ THUỘC
a. Với một điểm A và một đường thẳng d có thể xảy ra hai trường hợp:
• Điểm A thuộc đường thẳng d, kí hiệu a $\in$ d.
• Điểm A không thuộc đường thẳng d, kí hiệu a $\notin$ d.
b. Với một điểm A và một mặt phẳng $\alpha$ có thể xảy ra hai trường hợp:
• Điểm A thuộc mặt phẳng $\alpha$, kí hiệu a $\in$ $\alpha$.
• Điểm A không thuộc mặt phẳng $\alpha$, kí hiệu a $\notin$ $\alpha$.
2. CÁC TIÊN ĐỂ
Tiên đề 1: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
Tiên đề 2: Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Tiên đề 3: Nếu hai mặt phẳng có một điểm chung thì chúng còn có một điểm chung khác nữa.
Tiên đề 4: Có ít nhất bốn điểm không đồng phẳng.
3. NHỮNG KẾT QUẢ MỞ ĐẦU
Định lí 1: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất và chứa tất cả các điểm chung của hai mặt phẳng đó.
Khi đó, đường thẳng chung được gọi là giao tuyến của hai mặt phẳng.
Định lí 2: Có một và chỉ một mặt phẳng đi qua một đường thẳng và một điểm nằm ngoài đường thẳng đó.
Định lí 3: Có một và chỉ một mặt phẳng đi qua hai đường thẳng cắt nhau.
4. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Cho đường thẳng a và mặt phẳng $\alpha$. Căn cứ vào số điểm chung của đường thẳng và mặt phẳng ta có ba trường hợp sau:
a. Đường thẳng a và mặt phẳng $\alpha$ không có điểm chung, tức là:
$a\cap \alpha =\varnothing$ ⇔ a // $\alpha$
b. Đường thẳng a và mặt phẳng $\alpha$ chỉ có một điểm chung, tức là:
a $\cap$ $\alpha$ = {A} ⇔ a cắt $\alpha$ tại A.
c. Đường thẳng a và mặt phẳng $\alpha$ có 2 điểm chung phân biệt, tức là:
a $\cap$ $\alpha$ = {A, B} ⇔ a $\subset$ $\alpha$.

5. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI MẶT PHẲNG
Cho 2 mặt phẳng $\alpha$ và $\beta$. Căn cứ vào số đường thẳng chung của 2 mặt phẳng ta có ba trường hợp sau:
a. Hai mặt phẳng $\alpha$ và $\beta$ không có đường thẳng chung, tức là:
$\alpha \cap \beta =\varnothing$ ⇔ $\alpha$ // $\beta$
b. Hai mặt phẳng $\alpha$ và $\beta$ chỉ có một đường thẳng chung, tức là:
$\alpha \cap \beta =a$ ⇔ $\alpha$ cắt $\beta$.
c. Hai mặt phẳng $\alpha$ và $\beta$ có 2 đường thẳng chung phân biệt, tức là:
$\alpha \cap \beta$ = {a,b} ⇔ $\alpha$ $\equiv$ $\beta$
.png)
6. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG
Cho 2 đường thẳng a và b. Căn cứ vào sự đồng phẳng và số điểm chung của 2 đường thẳng ta có bốn trường hợp sau:
a. Hai đường thẳng song song: cùng nằm trong một mặt phẳng và không có điểm chung, tức là:
.png)
b. Hai đường thẳng cắt nhau: chỉ có một điểm chung.
a cắt b ⇔ a $\cap$ b = {l} .
c. Hai đường thẳng trùng nhau: có hai điểm chung phân biệt.
a $\cap$ b = {A, B} ⇔ a $\equiv$ b.
d. Hai đường thẳng chéo nhau: không cùng thuộc một mặt phẳng.
a chéo b ⇔ a, b không đồng phẳng.
.png)
7. CÁCH XÁC ĐỊNH ĐƯỜNG THẲNG VÀ MẶT PHẲNG
7.1. Cách xác định đường thẳng
Có ba cách xác định một đường thẳng:
Cách 1: Biết hai điểm phân biệt A, B của đường thẳng. Kí hiệu (AB).
Cách 2: Biết một điểm của đường thẳng và phương của đường thẳng đó.
Cách 3: Biết hai mặt phẳng phân biệt cùng chứa đường thẳng cần tìm.
7.2. Cách xác định mặt phẳng
Có bốn cách xác định một mặt phẳng:
Cách 1: Biết 3 điểm A, B, C không thẳng hàng của mặt phẳng, kí hiệu (ABC).
Cách 2: Biết 1 điểm A và một đường thẳng d không chứa A của mặt phẳng, kí hiệu (A, d).
Cách 3: Biết 2 đường thẳng cắt nhau a, b của mặt phẳng, kí hiệu (a, b).
Cách 4: Biết 2 đường thẳng song song a, b của mặt phẳng, kí hiệu (a, b).
B. PHƯƠNG PHÁP GIẢI TOÁN
Bài toán 1: Sử dụng các tiên đề xét vị trí tương đối của điểm, đường thẳng và mặt phẳng.
PHƯƠNG PHÁP CHUNG
1. Để biết khi nào một điểm thuộc một mặt phẳng, ta có các kết quả sau:
• Giả sử $\alpha$ là mặt phẳng xác định bởi ba điểm A, B, C thì khi đó A, B, C đều thuộc $\alpha$.
• Nếu đường thẳng a chứa trong mặt phẳng $\alpha$, thì khi đó điểm M thuộc a đều thuộc $\alpha$.
2. Để chứng minh đường thẳng a nằm trong mặt phẳng $\alpha$ ta đi chứng minh tồn tại hai điểm phân biệt A, B thuộc a và thuộc $\alpha$.
• Nếu mặt phẳng $\alpha$ cố định thì ta khẳng định được thêm rằng "Đường thẳng a nằm trong một mặt phẳng cố định $\alpha$".
• Nếu hai điểm A, B cố định thì ta khẳng định được thêm rằng " Mặt phẳng $\alpha$ chứa một đường thẳng cố định a".
3. Để chứng minh hai đường thẳng a, b chéo nhau, ta thường sử dụng phương pháp chứng minh phản chứng, cụ thể:
• Giả sử a, b không chéo nhau, tức là có một mặt phẳng $\alpha$ chứa cả a và b.
• Suy ra một kết luận vô lý (trái với giả thiết hoặc trái với các tiên đề, các định lí).
• Kết luận rằng hai đường thẳng a, b chéo nhau.
Ví dụ 1: Chứng minh rằng nếu ba đường thẳng phân biệt cắt nhau từng đôi một thì chúng đồng quy hoặc cùng nằm trong một mặt phẳng.
Giải
Với ba đường thẳng phân biệt a, b, c. Giả sử:
a $\cap$ b = {A}, b $\cap$ c = {B}, c $\cap$ a = {C}.
Xét hai trường hợp:
Trường hợp 1: Ba điểm A, B, C là ba điểm phân biệt.
Do a, b, c phân biệt nên A, B, C là ba điểm không thẳng hàng. Vậy chúng xác định một mặt phẳng (ABC). Ta có:
• Đường thẳng a có hai điểm A, C thuộc (ABC), nên a $\in$ (ABC).
• Tương tự b $\in$ (ABC) và c $\in$ (ABC).
Vậy, ba đường thẳng a, b, c cùng thuộc một mặt phẳng (ABC).
Trường hợp 2: Hai trong ba điểm A, B, C trùng nhau, giả sử A $\equiv$ B.
Nếu A $\neq$ C thì a $\equiv$ c, mâu thuẫn.
Do đó, ta phải có:
A $\equiv$ C ⇔ A $\equiv$ B $\equiv$ C ⇔ a, b, c đồng quy.
Vậy, ba đường thẳng a, b, c đồng quy.
Ví dụ 2: Trong mặt phẳng $\alpha$, cho góc $\widehat{xOy}$. A là điểm ngoài $\alpha$. M, N là hai điểm di động lần lượt trên Ox, Oy.
1. Giả sử OM = ON. Chứng minh rằng trung tuyến AP của $\Delta$AMN luôn nằm trong một mặt phẳng cố định.
2. Gọi d là đường thẳng cố định qua A và cắt $\alpha$ tại một điểm không thuộc Ox, Oy. MN di động nhưng luôn cắt d.
a. Chứng minh rằng MN luôn đi qua một điểm cố định.
b. Gọi B là điểm cố định trên d, B $\neq$ A và không thuộc $\alpha$. AM và BN cắt nhau tại Q. Chứng minh rằng Q thuộc đồng thời hai mặt phẳng cố định. Suy ra Q thuộc một đường thẳng cố định.
Giải
.png)
1. Ta có:
OM = ON ⇒ P thuộc Oz là tia phân giác của góc $\widehat{xOy}$ - cố định.
Vậy, trung tuyến AP nằm trong mặt phẳng cố định (A, Oz).
2. Giả sử d $\cap$ $\alpha$ = {P} – cố định.
a. Ta có ngay:
d $\cap$ MN = {P} cố định.
Vậy, đường thẳng MN luôn đi qua điểm cố định P.
b. Ta có:
• Q $\in$ BN $\subset$ (B, Oy) - cố định
⇒ Q $\in$ (B, Oy) - cố định.
• Q $\in$ AM $\subset$ (A, Ox) - cố định
⇒ Q $\in$ (A, Ox) - cố định.
Vậy, điểm Q thuộc đường thẳng cố định $\Delta$ là giao tuyến của hai mặt phẳng cố định (A, Ox) và (B, Oy).
Ví dụ 3: Trong mặt phẳng $\alpha$, cho hai nửa đường thẳng song song Ax, By. M và N là hai điểm lần lượt thuộc Ax và By; M $\neq$ A và N $\neq$ B. O là điểm cố định không thuộc $\alpha$.
a. Chứng minh rằng OA và MN chéo nhau.
b. M, N di động, chứng tỏ rằng đường thẳng OI nối O với trung điểm I của MN nằm trong mặt phẳng cố định.
c. M, N di động nhưng AM + BN có giá trị không đổi. Chứng minh rằng mặt phẳng (OMN) luôn chứa một đường thẳng cố định.
Giải
.png)
a. Ta đi chứng minh bằng phản chứng. Thật vậy, giả sử OA và MN không chéo nhau tức chúng cùng nằm trong một mặt phẳng. Mặt phẳng này chứa ba điểm A, M, N không thẳng hàng, đó chính là mặt phẳng $\alpha$, suy ra:
O $\in$ $\alpha$, trái với giả thiết.
Vậy, OA và MN chéo nhau.
b. Gọi C là trung điểm AB, nhận xét rằng:
ABNM là hình thang
⇒ I $\in$ Cz là đường trung bình của ABNM – cố định
Vậy, OI nằm trong mặt phẳng cố định (O, Cz).
c. Xét hình thang ABNM, ta có:
CI = $\large \frac{1}{2}$(AM + BN) – không đổi ⇒ I cố định.
Vậy, mặt phẳng (OMN) chứa đường thẳng OI cố định.
Ví dụ 4: Cho tứ diện ABCD. Gọi M, N là hai điểm phân biệt cùng thuộc đường thẳng AB; P, Q là hai điểm phân biệt cùng thuộc đường thẳng CD. Xét vị trí tương đối của hai đường thẳng MQ, NP và vị trí tương đối của hai đường thẳng MP, NQ.
Giải
.png)
a. Hai đường thẳng MQ, NP chéo nhau, bởi nếu trái lại tức là:
MQ và NP đồng phẳng
⇒ bốn điểm M, N, P, Q đồng phẳng
⇒ MN và PQ đồng phẳng
⇒ AB và CD đồng phẳng, điều này là mâu thuẫn.
b. Hai đường thẳng MP, NQ chéo nhau, bởi nếu trái lại tức là:
MP và NQ đồng phẳng ⇒ bốn điểm M, N, P, Q đồng phẳng
⇒ MN và PQ đồng phẳng ⇒ AB và CD đồng phẳng
điều đó là mâu thuẫn.
Ví dụ 5: Cho hai đường thẳng chéo nhau a, b. Trên a lấy hai điểm phân biệt A, B; trên b lấy hai điểm phân biệt C, D.
a. Chứng minh rằng AC và BD chéo nhau.
b. M là một điểm trên cạnh AC, N là một điểm trên cạnh BD. MN có thể song song với AB hoặc CD được không?
c. O là điểm trên đoạn MN. Chứng minh rằng AO cắt CN, và BO cắt DM.
Giải
.png)
a. Giả sử AC và BD không chéo nhau, suy ra:
AC và BD đồng phẳng ⇒ AB và CD đồng phẳng
điều này mâu thuẫn với giả thiết.
Vậy, ta có AC và BD chéo nhau.
b. MN không thể song song với AB hoặc CD bởi:
• Nếu MN // AB thì:
MN và AB đồng phẳng
⇒ AM và BN đồng phẳng
⇔ AC và BD đồng phẳng
điều đó mâu thuẫn.
• Nếu MN // CD thì:
MN và CD đồng phẳng
⇒ CM và DN đồng phẳng
⇔ AC và BD đồng phẳng, mâu thuẫn.
c. Ta lần lượt:
• Chứng minh AO cắt CN: Ta có:
O $\in$ MN ⇒ O $\in$ (CMN) và A $\in$ CM ⇒ A $\in$ (CMN)
⇒ AO và CN đồng phẳng.
Ngoài ra, AO và CN không thể song song với nhau bởi nếu:
AO // CN ⇒ O nằm ngoài đoạn MN, mâu thuẫn với giả thiết.
Vậy, ta có kết luận AO cắt CN.
• Tương tự ta chứng minh được BO cắt DM.
BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến $\Delta$. Trên (P) cho đường thẳng a và trên (Q) cho đường thẳng b. Chứng minh rằng nếu a và b cắt nhau thì hai giao điểm phải nằm trên $\Delta$.
Bài 2. Cho đường thẳng a nằm trong mặt phẳng $\alpha$ và một đường thẳng b cắt $\alpha$ tại điểm O. Chứng minh rằng nếu điểm O không thuộc a thì a và b chéo nhau
Bài 3. Cho đường thẳng a nằm trong mặt phẳng $\alpha$ và một đường thẳng b cắt $\alpha$ tại điểm O. Chứng minh rằng nếu điểm O không thuộc a thì a và b chéo nhau.
Bài 4. Chứng minh rằng có vô số đường thẳng cắt cả 3 đường thẳng cho trước đôi một chéo nhau.
Bài toán 2: Tìm giao tuyến của hai mặt phẳng.
PHƯƠNG PHÁP CHUNG
.png)
Để tìm giao tuyến của hai mặt phẳng, ta thực hiện theo các bước sau:
Bước 1: Tìm hai điểm chung của hai mặt phẳng.
Bước 2: Đường thẳng qua 2 điểm chung đó là giao tuyến.
Chú ý: Để tìm điểm chung của hai mặt phẳng ta thường tìm hai đường thẳng đồng phẳng lần lượt nằm trong hai mặt phẳng đó. Giao điểm, nếu có, của hai đường thẳng này chính là điểm chung của hai mặt phẳng.
Ví dụ 1: Trong mặt phẳng $\alpha$, cho tứ giác ABCD có AB cắt CD tại E, AC cắt BD tại F, S là một điểm không thuộc $\alpha$.
a. Tìm giao tuyến của (SAB) và (SCD).
b. Tìm giao tuyến của (SAC) và (SBD).
c. Tìm giao tuyến của (SEF) với các mặt phẳng (SAD) và (SBC).
Giải
.png)
a. Ta có ngay S là điểm chung của (SAB) và (SCD).
Mặt khác:
E $\in$ AB $\subset$ (SAB) ⇒ E $\in$ (SAB).
E $\in$ CD $\subset$ (SCD) ⇒ E $\in$ (SCD).
Vậy, ta được SE = (SAB) $\cap$ (SCD).
b. Tương tự câu a), ta được SF = (SAC) $\cap$ (SBD).
c. Giả sử EF cắt AD và BC theo thứ tự tại M, N. Khi đó:
• (SEF) và (SAD) có hai điểm chung là S và M nên có giao tuyến là SM.
• (SEF) và (SBC) có hai điểm chung là S và N nên có giao tuyến là SN.
Chú ý: Trong câu c) chúng ta đã sử dụng ý tưởng trong phần chú ý của bài toán 2 để thực hiện tìm điểm chung thứ hai, cụ thể:
• Trong mặt phẳng (SEF) ta chọn đường thẳng EF.
• Trong mặt phẳng (SBC) ta chọn đường thẳng BC.
• Ta có EF và BC cùng nằm trong mặt phẳng (ABCD) và EF $\cap$ BC = {N}.
• Do đó N là điểm chung của hai mặt phẳng (SEF) và (SBC).
Đối với ví dụ trên, điều này rất trực quan và thấy ngay được. Tuy nhiên, một vài bài toán các em học sinh cần hiểu được bản chất của vấn đề mới có được lựa chọn thích hợp.
Ví dụ 2: Trong mặt phẳng $\alpha$, cho hình bình hành ABCD tâm O, S là một điểm không thuộc $\alpha$. Gọi M, N, P lần lượt là trung điểm của BC, CD, SO. Tìm giao tuyến của mặt phẳng (MNP) với các mặt phẳng (SAB), (SAD), (SBC) và (SCD).
Giải
.png)
Đường thẳng MN cắt AB, AD và AC tại $M_{1}$, $N_{1}$ và $O_{1}$. Khi đó:
• Nối $O_{1}P$ cắt SA tại $P_{1}$.
• Nối $M_{1}P_{1}$ cắt SB tại $M_{2}$
• Nối $N_{1}P_{1}$ cắt SD tại $N_{2}$.
Vậy, ta được:
(MNP) $\cap$ (SAB) = $P_{1}M_{2}$.
(MNP) $\cap$ (SAD) = $P_{1}N_{2}$.
(MNP) $\cap$ (SBC) = $MM_{2}$.
(MNP) $\cap$ (SCD) = $NN_{2}$.
Ví dụ 3: Trong mặt phẳng $\alpha$, cho tứ giác ABCD có AB cắt CD, S là một điểm không thuộc $\alpha$. Gọi C' là một điểm nằm giữa S và C. Hãy tìm giao tuyến của mặt phẳng (ABC') với các mặt phẳng (ABCD), (SAB), (SBC), (SCD), (SAD).
Giải
.png)
Ta có thể trình bày theo hai cách sau:
Cách 1: Từ giả thiết, giả sử AB cắt CD tại M.
Nối MC' cắt SD tại D', khi đó ta nhận được:
(ABC') $\cap$ (ABCD) = AB,
(ABC') $\cap$ (SAB) = AB,
(ABC') $\cap$ (SBC) = BC',
(ABC') $\cap$ (SCD) = C'D',
(ABC') $\cap$ (SAD) = AD'.
Cách 2: Giả sử AC cắt BD tại O.
Trong mặt phẳng (SAC), ta có AC' $\cap$ SO = {I}.
Nối BI cắt SD tại D', khi đó ta nhận được:
(ABC') $\cap$ (ABCD) = AB,
(ABC') $\cap$ (SAB) = AB,
(ABC') $\cap$ (SBC) = BC',
(ABC') $\cap$ (SCD) = C'D',
(ABC') $\cap$ (SAD) = AD'.
BÀI TẬP ĐỀ NGHỊ
Bài 5. Trong mặt phẳng $\alpha$, cho $\Delta$ABC, D là một điểm không thuộc $\alpha$. Gọi I, J lần lượt là trung điểm của AC và BC. K là điểm trên cạnh BD sao cho KD < KB. Tìm giao tuyến của mặt phẳng (IJK) với các mặt phẳng (ACD) và (ABD).
Bài 6. Trong mặt phẳng $\alpha$, cho $\Delta$ABC, D là một điểm không thuộc $\alpha$. M là một điểm bên trong $\Delta$ABD, N là một điểm bên trong $\Delta$ACD.
a. Tìm giao tuyến của (AMN) và (BCD).
b. Tìm giao tuyến của (DMN) và (ABC).
Bài 7. Trong mặt phẳng $\alpha$, cho $\Delta$ABC, D là một điểm không thuộc $\alpha$. O là điểm bên trong $\Delta$BCD, M là điểm trên AO.
a. Tìm giao tuyến của (MCD) với các mặt phẳng (ABC) và (ABD).
b. I, J là hai điểm trên BC và BD. Tìm giao tuyến của (IJM) và (ACD).
Bài 8. Trong mặt phẳng $\alpha$, cho hình bình hành ABCD tâm O, S là một điểm không thuộc $\alpha$. M, N lần lượt là trung điểm của SB, SD, P là điểm trên SC và SP > PC. Tìm giao tuyến của (MNP) với các mặt phẳng (SAB), (SAD), (SAC) và (ABCD).
Bài toán 3: Chứng minh ba điểm thẳng hàng.
Ba đường thẳng đồng quy.
PHƯƠNG PHÁP CHUNG
1. Để chứng minh 3 điểm thẳng hàng, ta chứng minh chúng cùng thuộc hai mặt phẳng phân biệt. Khi đó chúng thuộc giao tuyến của hai mặt phẳng đó.
.png)
2. Để chứng minh 3 đường thẳng đồng quy, ta chứng minh giao điểm của hai đường thẳng này là điểm chung của hai mặt phẳng mà giao tuyến là đường thẳng thứ ba.
.png)
Ví dụ 1: Cho mặt phẳng $\alpha$ và ba điểm A, B, C không thẳng hàng ở ngoài $\alpha$. Giả sử các đường thẳng BC, CA, AB lần lượt cắt $\alpha$ tại D, E, F. Chứng minh ba điểm D, E, F thẳng hàng.
Giải
.png)
Trước tiên, ta thấy ngay ba điểm D, E, F thuộc mặt phẳng $\alpha$. Mặt khác, ta có:
D $\in$ BC $\subset$ (ABC) ⇒ D $\in$ (ABC).
E $\in$ CA $\subset$ (ABC) ⇒ E $\in$ (ABC).
F $\in$ AB $\subset$ (ABC) ⇒ F $\in$ (ABC).
Vậy, ta được:
(ABC) $\cap$ $\alpha$ = {D, E, F} ⇒ D, E, F thẳng hàng.
Ví dụ 2: Cho mặt phẳng (P) và 2 điểm A, B cố định ở ngoài (P) sao cho đường thẳng AB cắt mặt phẳng (P) tại điểm C. M là điểm di động trong không gian sao cho MA, MB cắt (P) tại $A_{1}$, $B_{1}$. Chứng minh $A_{1}B_{1}$ luôn đi qua một điểm cố định.
Giải
.png)
Trước tiên, ta thấy C là một điểm cố định.
Nhận xét rằng:
A $\cap$ (MAB) = {$A_{1}$, $B_{1}$, C}
⇒ $A_{1}$, $B_{1}$, C thẳng hàng ⇔ $A_{1}B_{1}$ luôn đi qua điểm cố định C.
Ví dụ 3: Trong mặt phẳng $\alpha$, cho $\Delta$BCD, A là một điểm không thuộc $\alpha$. Gọi E, F, G lần lượt là 3 điểm trên 3 cạnh AB, AC, BD sao cho EF cắt BC tại I, EG cắt AD tại H. Chứng minh CD, IG, HF đồng quy.
Giải
.png)
Gọi O là giao điểm của HF và IG. Ta có:
O $\in$ HF $\subset$ (ACD) ⇒ O $\in$ (ACD).
O $\in$ IG $\subset$ (BCD) ⇒ O $\in$ (BCD).
Suy ra:
O $\in$ (ACD) $\cap$ (BCD) = CD.
Vậy, ba đường thẳng CD, IG, HF đồng quy tại O.
Ví dụ 4: Trong mặt phẳng $\alpha$, cho tứ giác ABCD, S là một điểm không thuộc $\alpha$. Gọi I, J là hai điểm cố định trên SA và SC với SI > IA và SJ < JC. Một mặt phẳng $\beta$ quay quanh IJ cắt SB tại M, SD tại N.
a. Chứng minh rằng IJ, MN và SO đồng quy (với O là giao điểm của AC và BD). Suy ra cách dựng điểm N khi biết điểm M.
b. AD cắt BC tại E, IN cắt MJ tại F. Chứng minh S, E, F thẳng hàng.
.png)
c. Trước tiên, vì IJ không song song với AC nên:
IJ $\cap$ AC = T - là một điểm cố định.
Nhận xét rằng:
$\beta$ $\cap$ (ABCD) = {T, P, Q} = T, P, Q thẳng hàng
⇔ PQ luôn đi qua điểm cố định T.
BÀI TẬP ĐỀ NGHỊ
Bài 9. Cho hai điểm A và B nằm trong mặt phẳng $\alpha$ và một điểm O nằm ngoài $\alpha$. Lấy M, N theo thứ tự thuộc OA và OB, với M $\neq$ O, M $\neq$ A, N $\neq$ O, N $\neq$ A. Giả sử MN cắt $\alpha$ tại C. Chứng minh rằng ba điểm A, B, C thẳng hàng.
Bài 10. Trong mặt phẳng $\alpha$, cho $\Delta$ABC, D là một điểm không thuộc $\alpha$. Qua C dựng mặt phẳng $\gamma$ cắt AB, BD tại $B_{1}$, $B_{2}$, qua B dựng mặt phẳng $\beta$ cắt AC, CD tại $C_{1}$, $C_{2}$. $BB_{1}$, $CC_{1}$ cắt nhau tại $O_{1}$; $BB_{2}$, $CC_{2}$ cắt nhau tại $O_{2}$. Giả sử $O_{1}O_{2}$ kéo dài cắt SA tại I.
a. Chứng minh $AO_{1}$, $DO_{2}$, BC đồng quy.
b. Chứng minh I, $B_{1}$, $B_{2}$ và I, $C_{1}$, $C_{2}$ thẳng hàng.
Bài toán 4: Tìm giao điểm của đường thẳng và mặt phẳng.
PHƯƠNG PHÁP CHUNG
Cho đường thẳng a và mặt phẳng $\alpha$, giả sử a cắt $\alpha$. Để tìm giao điểm A của a và $\alpha$, ta lựa chọn một trong hai hướng sau:
.png)
Hướng 1: Nếu trong mặt phẳng $\alpha$ có sẵn một đường thẳng c cắt a tại điểm A nào đó thì A chính là giao điểm của a và $\alpha$.
Hướng 2: Thực hiện theo các bước:
Bước 1: Chọn mặt phẳng phụ $\beta$ chứa a sao cho giao tuyến c của $\alpha$ và $\beta$ dễ xác định.
Bước 2: Trong $\beta$, đường thẳng c cắt a tại điểm A nào đó thì A là giao điểm của a và $\alpha$.
Ví dụ 1: Cho bốn điểm A, B, C, D không đồng phẳng. Gọi M, N lần lượt là trung điểm của AC và BC. Trên BD lấy điểm P sao cho BP = 2PD.
a. Tìm giao điểm của đường thẳng CD với mặt phẳng (MNP).
b. Tìm giao tuyến của hai mặt phẳng (MNP) và (ACD).
Giải
.png)
a. Từ giả thiết về điểm N và P ta gọi:
Q = CD $\cap$ NP $\subset$ (MNP)
⇒ Q = CD $\cap$ (MNP).
b. Ta có ngay:
(MNP) $\cap$ (ACD) = MQ.
Ví dụ 2: Trong mặt phẳng $\alpha$, cho tứ giác ABCD, S là một điểm không thuộc $\alpha$ . Gọi M là một điểm nằm trong $\Delta$SCD.
a. Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC).
b. Tìm giao điểm của đường thẳng BM và mặt phẳng (SAC).
c. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (ABM).
Giải
.png)
a. Ta lần lượt thực hiện:
• Kéo dài SM cắt cạnh BC tại N.
• Nối BN cắt AC tại O.
Khi đó:
(SBM) $\cap$ (SAC) = SO.
b. Nối BM cắt cạnh SC tại I.
Vậy, ta được I chính là giao điểm của BM và (SAC)
c. Ta lần lượt thực hiện:
• Nối AI cắt SC tại E.
• Nối EM cắt SD tại F.
Khi đó, các đoạn thẳng AB, BE, EF, FA là các đoạn giao tuyến của mặt phẳng (ABM) với hình chóp.
Vậy, thiết diện là tứ giác ABEF.
Ví dụ 3: Trong mặt phẳng $\alpha$, cho tứ giác ABCD, S là một điểm không thuộc $\alpha$. M là điểm trên cạnh SC.
a. Tìm giao điểm của AM và (SBD).
b. Gọi N là một điểm trên cạnh BC, tìm giao điểm của SD và (AMN).
Giải
.png)
a. Chọn mặt phẳng phụ (SAC) chứa AM.
Gọi O là giao điểm của AC và BD, suy ra:
(SAC) $\cap$ (SBD) = SO.
Trong mặt phẳng (SAC), ta có:
SO $\cap$ AM = $O_{1}$ ⇒ AM $\cap$ (SBD) = $O_{1}$
b. Chọn mặt phẳng phụ (SBD) chứa SD
Gọi $N_{1}$ là giao điểm của AN và BD, suy ra:
(SBD) $\cap$ (AMN) = $N_{1}O_{1}$
Trong mặt phẳng (SBD), ta có:
$N_{1}O_{1}$ $\cap$ SD = $D_{1}$ ⇒ SD $\cap$ (AMN) = $D_{1}$.
BÀI TẬP ĐỀ NGHỊ
Bài 11. Cho bốn điểm A, B, C, D không đồng phẳng. Trên AC và AD lần lượt lấy các điểm M, N sao cho MN không song song với CD. Gọi O là một điểm bên trong $\Delta$BCD.
a. Tìm giao tuyến của (OMN) và (BCD).
b. Tìm giao điểm của BC và BD với (OMN).
Bài 12. Cho bốn điểm A, B, C, D không đồng phẳng. Trên AC và AD lần lượt lấy các điểm M, N. Gọi O là một điểm bên trong $\Delta$BCD.
a. Tìm giao điểm của MN và (ABO).
b. Tìm giao điểm của AO và (BMN).
Bài 13. Cho bốn điểm A, B, C, D không đồng phẳng. Lấy I, J lần lượt là hai điểm bên trong $\Delta$ABC và $\Delta$ABD. M là điểm tuỳ ý trên CD. Tìm giao điểm của IJ và (ABM).
Bài 14. Trong mặt phẳng $\alpha$, cho hình thang ABCD đáy lớn AB. S là một điểm không thuộc $\alpha$. Gọi I, J, K theo thứ tự là ba điểm thuộc SA, AB, BC.
a. Tìm giao điểm của IK và (SBD).
b. Tìm giao điểm của (IJK) với SD và SC.
Bài toán 5: Bài toán dựng hình.
PHƯƠNG PHÁP CHUNG
Ta thường thực hiện theo bốn bước đã biết.
Ví dụ 1: Cho hai đường thẳng a, b chéo nhau và một điểm M không thuộc hai đường thẳng đó. Hãy dựng một đường thẳng qua M cắt cả hai a, b.
Giải
.png)
a. Phân tích: Giả sử dụng được đường thẳng d qua M cắt a, b theo thứ tự tại A và B, khi đó:
M, A thuộc d, nên d $\in$ (M, a).
M, B thuộc d, nên d $\in$ (M, b).
Suy ra d = (M, a) $\cap$ (M, b).
b. Cách dựng: Ta lần lượt thực hiện:
• Dựng mặt phẳng (M, a).
• Dựng mặt phẳng (M, b).
• Xác định giao tuyến d của hai mặt phẳng (M, a) và (M, b).
Khi đó d là đường thẳng cần dựng.
c. Chứng minh: Ta thấy:
d = (M, a) $\cap$ (M, b), nên d đi qua M.
d, a thuộc (M, a), nên chúng có thể cắt nhau tại A.
d, b thuộc (M, b), nên chúng có thể cắt nhau tại B.
Vậy, d đi qua M có thể cắt cả a và b.
d. Biện luận: Nhận thấy:
• Nếu d cắt a và d cắt b, ta có ngihiệm duy nhất.
• Nếu d // a hoặc d // b, bài toán vô nghiệm.
BÀI TẬP ĐỀ NGHỊ
Bài 15. Cho bốn điểm A, B, C, D không đồng phẳng. O là điểm bên trong ABCD, M là điểm trên AB
a. Hãy dựng đường thẳng qua M cắt AO và CD.
b. N là điểm trên BC và ON không song song với BD. Dựng đường thẳng qua N cắt AO và DM.
Bài 16. Hãy nêu cách dựng một đường thẳng cắt cả 3 đường thẳng cho trước đôi một chéo nhau cho trước.
Bài toán 6: (Bài toán quỹ tích): Tìm tập hợp giao điểm của hai đường thẳng di động.
PHƯƠNG PHÁP CHUNG
Gọi M là giao điểm hai đường thẳng di động $d_{1}$, $d_{2}$. Để tìm tập hợp các điểm M ta thực hiện theo các bước sau:
Bước 1: Phần thuận: Tìm hai mặt phẳng cố định lần lượt chứa $d_{1}$ và $d_{2}$. M di động trên giao tuyến cố định d của hai mặt phẳng đó.
Bước 2: Giới hạn (nếu có) được tập $\bar{d}$.
Bước 3: Phần đảo: Gọi M là điểm bất kỳ trên $\bar{d}$, ta đi chứng minh M là giao điểm của hai đường thẳng $d_{1}$ và $d_{2}$.
Bước 4: Kết luận.
Chú ý: Nếu d di động nhưng luôn đi qua điểm cố định A và cắt đường thẳng cố định a không qua A thì d thuộc mặt phẳng cố định (A, a).
Ví dụ 1: Trong mặt phẳng $\alpha$, cho tứ giác ABCD có AB và CD không song song. S là một điểm không thuộc $\alpha$, M là điểm di động trên cạnh SB. Mặt phẳng (ADM) cắt SC tại N. Tìm tập hợp giao điểm của AM và DN.
Giải
.png)
Phần thuận: Ta có:
AM $\subset$ (SAB) - cố định.
Mặt khác, vì DN đi qua điểm cố định D và cắt đường thẳng cố định SC nên:
DN $\subset$ (SCD) - cố định.
Giả sử AB cắt CD tại O, ta có ngay:
(SAB) $\cap$ (SCD) = SO.
Vậy, tập hợp giao điểm P của AM và định nghĩa thuộc đường thẳng SO
Giới hạn: Khi M di chuyển trên cạnh SB thì P di chuyển trên đoạn SO.
Phần đảo: Gọi P là điểm bất kỳ trên SO.
• Nối AP cắt SB tại M.
• Nối DP cắt SC tại N, N là giao điểm của mặt phẳng (ADM) với SC và P chính là giao điểm của AM và DN.
Kết luận: Vậy tập hợp các điểm P là đoạn SO.
Ví dụ 2: Trong mặt phẳng $\alpha$, cho tứ giác ABCD, AB và CD kéo dài cắt nhau tại E, AD và BC kéo dài cắt nhau tại F và AD < DF. S là một điểm không thuộc $\alpha$. Gọi I, J lần lượt là trung điểm của SA, SB. $\alpha$ là mặt phẳng di động qua IJ. $\alpha$ cắt SC, SD lần lượt tại M, N
a. Chứng minh rằng J, MN, SE đồng quy.
b. M chuyển động trên phần nào của cạnh SC?
c. Tìm tập hợp giao điểm của IM và JN.
d. Tìm tập hợp giao điểm của IN và JM.
Giải
.png)
a. Gọi K = IJ $\cap$ MN, ta có:
K $\in$ IJ $\subset$ (SAB) ⇒ K $\in$ (SAB).
K $\in$ MN $\subset$ (SCD) ⇒ K $\in$ (SCD).
Do đó K $\in$ SE = (SAB) $\cap$ (SCD).
Vậy, ba đường thẳng IJ, MN, SE đồng quy tại K.
b. Nối KD cắt SC tại $M_{0}$. Vì N chạy trên cạnh SD nên tia KMN quét góc $\widehat{SKD}$, do đó M chạy từ S đến $M_{0}$ vì khi đó $\alpha$ mới cắt cạnh SC, SD.
c.
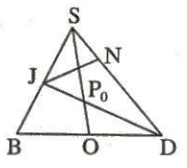
Gọi P = IM $\cap$ JN. Ta đi tìm tập hợp điểm P.
Phần thuận: Ta có:
P $\in$ IM $\subset$ (SAC) ⇒ P $\in$ (SAC).
P $\in$ JN $\subset$ (SBD) ⇒ P $\in$ (SBD).
Do đó:
P $\in$ SO = (SAC) $\cap$ (SBD).
Giới hạn: Nối DJ cắt SO tại $P_{0}$. Vì N chạy trên cạnh SD nên tia JPN quét góc $\widehat{SJD}$, do đó P chạy từ S đến $P_{0}$ vì khi đó $\alpha$ mới cắt cạnh SC, SD.
Phần đảo. Gọi P là điểm bất kỳ trên $SP_{0}$. Nối JP cắt SD tại N, nối IP cắt SC tại M. M, N là giao điểm của mặt phẳng (IJMN) qua IJ với các cạnh SC, SD và P chính là giao điểm của IM và JN.
Kết luận: Vậy tập hợp các điểm P là đoạn $SP_{0}$ trên SO.
d. Gọi Q = IN $\cap$ JM. Ta đi tìm tập hợp điểm Q.
Phần thuận: Ta có:
Q $\in$ IN $\subset$ (SAD) ⇒ Q $\in$ (SAD).
Q $\in$ JM $\subset$ (SBC) ⇒ Q $\in$ (SBC).
Do đó:
Q $\in$ SF = (SAD) $\cap$ (SBC).
Giới hạn: Vì AD < DF, nên tia Ix song song với SF và cắt cạnh SD tại $N_{0}$. Vậy N chạy từ S tới $N_{0}$. Nối $IN_{0}$ cắt SF tại $F_{0}$, do đó Q chạy từ S đến $F_{0}$.
Phần đảo: Gọi Q là điểm bất kỳ trên $SF_{0}$. Nối IQ cắt SD tại N, nối JQ cắt SC tại M. M, N là giao điểm của mặt phẳng (IJMN) qua IJ với các cạnh SC, SD và Q chính là giao điểm của IN và JM.
Kết luận: Vậy tập hợp các điểm Q là đoạn $SF_{0}$ trên SF.
BÀI TẬP ĐỀ NGHỊ
Bài 17. Khi giải một bài toán, một học sinh đã vẽ tứ diện, trong đó đã dựng một thiết diện (hình dưới). Hình vẽ có đúng không ?
.png)
Bài 18. Cho bốn điểm A, B, C, D không đồng phẳng. Gọi I, J là hai điểm cố định trên AB, AC và IJ không song song với BC. $\alpha$ là mặt phẳng quay quanh IJ. $\alpha$ cắt CD, BD lần lượt tại M, N.
a. Chứng minh rằng MN luôn đi qua một điểm cố định.
b. Tìm tập hợp giao điểm của IM và JN.
c. Tìm tập hợp giao điểm của IN và JM.
Bài 19. Trong mặt phẳng $\alpha$ cho hai đường thẳng d, d' cắt nhau tại O. A, B là hai điểm cố định ở ngoài $\alpha$ và AB không song song với $\alpha$. Một mặt phẳng $\beta$ quay quanh AB cắt d tại M và d' tại N. Chứng minh rằng:
a. MN luôn đi qua một điểm cố định.
b. Giao điểm I của AM và BN ở trên đường thẳng cố định.
c. Giao điểm J của AN và BM ở trên đường thẳng cố định.
d. IJ luôn đi qua một điểm cố định.
Bài 20. Trong mặt phẳng $\alpha$, cho hình thang ABCD có các cạnh đáy là AB và CD với AB = 2CD. S là một điểm không thuộc $\alpha$. Gọi I là trung điểm của SA, J là một điểm trên cạnh SC với JS > JC.
a. $\beta$ là mặt phẳng quay quanh IJ, cắt SD, SB theo thứ tự tại M, N. M,N di động trên phần nào của đoạn SD, SB ? Tìm tập hợp giao điểm của IM và JN.
b. $\gamma$ là mặt phẳng quay quanh IJ cắt AD tại P. Tìm giao điểm Q của $\gamma$ và cạnh CD và tập hợp giao điểm của IQ và JP.
