§7. HÌNH CHÓP CỤT
A. TÓM TẮT LÍ THUYẾT
1. ĐỊNH NGHĨA
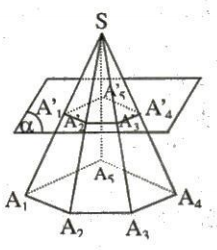
Cho hình chóp $SA_{1}A_{2}...A_{n}$. Một mặt phẳng $\alpha$ song song với mặt phẳng chứa đa giác đáy cắt các cạnh $SA_{1}$, $SA_{2}$, ..., $SA_{n}$ theo thứ tự tại $A'_{1}$, $A'_{2}$, ..., $A'_{n}$. Hình tạo bởi thiết diện $A'_{1}A'_{2}...A'_{n}$ và đáy $A_{1}A_{2}...A_{n}$ của hình chóp cùng với các mặt bên $A_{1}A_{2}A'_{2}A'_{1}$, $A_{2}A_{3}A'_{3}A'_{2}$, ..., $A_{n}A_{1}A'_{1}A'_{n}$ gọi là một hình chóp cụt.
Trong đó:
• Đáy của hình chóp gọi là đáy lớn của hình chóp cụt, còn thiết diện gọi là đáy nhỏ của hình chóp cụt.
• Các mặt còn lại gọi là các mặt bên của hình chóp cụt.
• Cạnh chung của hai mặt bên kề nhau như $A_{1}A'_{1}$, $A_{2}A'_{2}$, ..., $A_{n}A'_{n}$ gọi là cạnh bên của hình chóp cụt.
Tuỳ theo đáy là tam giác, tứ giác, ngũ giác, ... ta có hình chóp cụt tam giác, hình chóp cụt tứ giác, hình chóp cụt ngũ giác, ...
2. TÍNH CHẤT
Với hình chóp cụt, ta có các tính chất sau:
1. Hai đáy của hình chóp cụt là hai đa giác đồng dạng.
2. Các mặt bên của hình chóp cụt là các hình thang.
3. Cách cạnh bên của hình chóp cụt đồng quy tại một điểm.
Chứng minh
1. Vì $\alpha$ // ($A_{1}A_{2}...A_{n}$) nên (theo định lí " Nếu hai mặt phẳng song song bị cắt bởi một mặt phẳng thứ ba thì hai giao tuyến song song với nhau"):
$A_{1}A_{2}$ // $A'_{1}A'_{2}$
$A_{2}A_{3}$ // $A'_{2}A'_{3}$
...
$A_{n-1}A_{n}$ // $A'_{n-1}A'_{n}$
nên hai đa giác $A_{1}A_{2}...A_{n}$ và $A'_{1}A'_{2}...A'_{n}$ đồng dạng với nhau.
2. Lập luận như 1) ta thấy ngay các mặt bên của hình chóp cụt là các hình thang.
3. Các cạnh bên của hình chóp cụt đồng quy tại một điểm theo định nghĩa.
B. VÍ DỤ MINH HOẠ
Ví dụ 1: Cho hình chóp cụt $ABC.A_{1}B_{1}C_{1}$ trong đó ABC là đáy lớn. Gọi M, N, P theo thứ tự là trung điểm AB, BC, CA và $M_{1}$, $N_{1}$, $P_{1}$ theo thứ tự là trung điểm $A_{1}B_{1}$, $B_{1}C_{1}$, $C_{1}A_{1}$
a. Chứng minh rằng các đường thẳng $MM_{1}$, $NN_{1}$, $PP_{1}$ đồng quy.
b. Chứng minh rằng MN // $M_{1}N_{1}$, NP // $N_{1}P_{1}$, PM // $P_{1}M_{1}$.
Giải
.png)
a. Gọi S là điểm đồng quy của các đường thẳng $AA_{1}$, $BB_{1}$, $CC_{1}$, ta có:
AB // $A_{1}B_{1}$
M, $M_{1}$ theo thứ tự là trung điểm của AB, $A_{1}B_{1}$ suy ra S $\in$ $MM_{1}$.
Tương tự, ta cũng có S $\in$ $NN_{1}$ và S $\in$ $PP_{1}$
Vậy, các đường thẳng $MM_{1}$, $NN_{1}$, $PP_{1}$ đồng quy tại S.
b. Theo tính chất đường trung bình, ta có:
MN // AC
$M_{1}N_{1}$ // $A_{1}C_{1}$
ngoài ra, theo tính chất hình chóp cụt AC // $A_{1}C_{1}$ nên MN // $M_{1}N_{1}$.
Tương tự, ta cũng có NP // $N_{1}P_{1}$, PM // $P_{1}M_{1}$.
BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho hình chóp cụt $ABCD.A_{1}B_{1}C_{1}D_{1}$ trong đó ABCD là đáy lớn có diện tích bằng $s_{1}$ và $A_{1}B_{1}C_{1}D_{1}$ là đáy nhỏ có diện tích bằng $s_{2}$.
a. Gọi S là điểm đồng quy của các đường thẳng $AA_{1}$, $BB_{1}$, $CC_{1}$, $DD_{1}$.
Chứng minh rằng:
.png)
b. Gọi M là trung điểm $AA_{1}$, mặt phẳng $\alpha$ qua M và song song với mặt phẳng đáy (ABCD). Xác định thiết diện của hình chóp cụt với mặt phẳng $\alpha$. Tính diện tích thiết diện theo $s_{1}$ và $s_{2}$
Bài 2. Cho hình chóp cụt $ABCD.A_{1}B_{1}C_{1}D_{1}$ trong đó đáy lớn ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là các giao điểm của các cặp đường thẳng $AD_{1}$ và $BC_{1}$, $CB_{1}$ và $DA_{1}$, $BA_{1}$ và $CD_{1}$, $AB_{1}$ và $DC_{1}$. Chứng minh rằng bốn điểm M, N, P, Q đồng phẳng.
