§5. KHOẢNG CÁCH

A. TÓM TẮT LÍ THUYẾT

1. KHOẢNG CÁCH TỪ MỘT ĐIỂM TỚI MỘT ĐƯỜNG THẲNG

Trong không gian cho điểm O và đường thẳng d, kẻ OH $\perp$ d với H $\in$ d.

Định nghĩa: Độ dài đoạn OH được gọi là khoảng cách từ điểm O tới đường thẳng d.

Nhận xét:

• Khoảng cách từ điểm O tới đường thẳng d là bé nhất so với khoảng cách từ O đến mọi điểm của d.

• Khoảng cách từ điểm O tới đường thẳng d bằng 0 khi và chỉ khi O $\in$ d.

2. KHOẢNG CÁCH TỪ MỘT ĐIỂM TỚI MỘT MẶT PHẲNG

Trong không gian cho điểm O và mặt phẳng $\alpha$, gọi H là hình chiếu vuông góc của O trên $\alpha$.

Định nghĩa: Độ dài đoạn OH được gọi là khoảng cách từ điểm O tới mặt phẳng $\alpha$.

Nhận xét:

• Khoảng cách từ điểm O tới mặt phẳng $\alpha$ là bé nhất so với khoảng cách từ O đến mọi điểm của $\alpha$.

• Khoảng cách từ điểm O tới mặt phẳng $\alpha$ bằng O khi và chỉ khi O $\in$ $\alpha$.

3. KHOẢNG CÁCH GIỮA MỘT ĐƯỜNG THẲNG VÀ MỘT MẶT PHẲNG SONG SONG

Trong không gian cho đường thẳng d song song với mặt phẳng $\alpha$. Lấy điểm A bất kì trên d, gọi H là hình chiếu vuông góc của A trên $\alpha$.

Định nghĩa: Độ dài đoạn AH được gọi là khoảng cách từ đường thẳng d tới mặt phẳng $\alpha$.

Nhận xét: Khoảng cách từ đường thẳng d tới mặt phẳng $\alpha$ là bé nhất so với khoảng cách từ một điểm tuỳ ý thuộc d tới một điểm bất kì của $\alpha$.

4. KHOẢNG CÁCH GIỮA HAI MẶT PHẲNG SONG SONG

Trong không gian cho hai mặt phẳng $\alpha$, $\beta$ song song với nhau.

Định nghĩa: Khoảng cách từ một điểm tuỳ ý của $\alpha$ tới $\beta$ được gọi là khoảng cách giữa hai mặt phẳng $\alpha$ và $\beta$.

Nhận xét: Khoảng cách giữa hai mặt phẳng $\alpha$ và $\beta$ là bé nhất so với khoảng cách từ một điểm tuỳ ý thuộc $\alpha$ tới một điểm bất kì của $\beta$.

5. ĐƯỜNG VUÔNG GÓC CHUNG VÀ KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẮNG CHÉO NHAU

Định lí: Cho hai đường thẳng chéo nhau a và b, luôn có duy nhất một đường thẳng d cắt cả a và b, và vuông góc với mỗi đường thẳng ấy. Đường thẳng d được gọi là đường vuông góc chung của a và b.

Giả sử d cắt a, b theo thứ tự tại M và N.

Định nghĩa: Đoạn MN được gọi là đoạn vuông góc chung của a và b. Độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b.

Nhận xét: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa:

• Một trong hai đường thẳng đó và mặt phẳng song song với nó chứa đường thẳng còn lại.

• Hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.

Từ đó suy ra " Khoảng cách giữa hai đường thẳng chéo nhau là bé nhất so với khoảng cách giữa hai điểm bất kì lần lượt nằm trên hai đường thẳng ấy".

B. PHƯƠNG PHÁP GIẢI TOÁN

Bài toán 1: Khoảng cách từ một điểm tới một đường thẳng.

PHƯƠNG PHÁP CHUNG

Để tính khoảng cách từ điểm O tới đường thẳng d, ta thực hiện theo các bước sau:

Bước 1: Trong mặt phẳng (O, d) hạ OH $\perp$ d với H $\in$ d.

Bước 2: Thực hiện việc xác định độ dài OH dựa trên hệ thức lượng trong tam giác, tứ giác và đường tròn.

Chú ý:

1.

Nếu tồn tại đường thẳng a qua O và song song với d thì:

d(O, d) = d(A, d), với A $\in$ d

2.

Nếu AO $\cap$ d = I thì:

Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O, SA = a và vuông góc với mặt phẳng (ABCD). Gọi I, M theo thứ tự là trung điểm của SC, AB.

a. Chứng minh rằng OI $\perp$ (ABCD).

b. Tính khoảng cách từ I đến đường thẳng CM, từ đó suy ra khoảng cách từ S tới CM.

Giải

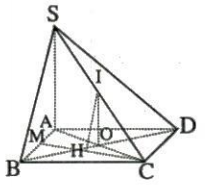
a. Trong $\Delta$SAC, ta có:

OI là đường trung bình

⇒ OI // SA ⇒ OI $\perp$ (ABCD).

b. Gọi H là hình chiếu vuông góc của I lên CM, ta có:

Trong $\Delta$ABC có K là trọng tâm, ta có:

Trong $\Delta$OCK vuông tại O, ta có:

Trong $\Delta$OIH vuông tại O, ta có:

Vậy, khoảng cách từ I tới CM bằng

Vì SI $\cap$ CM = C nên:

Ví dụ 2: Cho hình chóp S.ABC có SA = 2a và vuông góc với mặt phẳng (ABC), $\Delta$ABC vuông tại C với AB = 2a, $\widehat{BAC}$ = 30°. Gọi M là một điểm di động trên cạnh AC, H là hình chiếu vuông góc của S trên BM.

a. Chứng minh rằng AH $\perp$ BM.

b. Đặt AM = x, với 0 $\leq$ x $\leq$ $\sqrt{3}$. Tính khoảng cách từ S đến BM theo a và x. Tìm các giá trị của x để khoảng cách này có giá trị nhỏ nhất, lớn nhất.

Giải

a. Vì SA $\perp$ (ABC) nên AH là hình chiếu vuông góc của SH trên (ABC), do đó:

AH $\perp$ BM, theo định lí ba đường vuông góc.

b. Ta thấy ngay khoảng cách từ S đến BM chính là SH và trong $\Delta$SAH ta có:

(1)

Trong $\Delta$ABC vuông tại C có $\widehat{BAC}$ = 30° nên:

Trong $\Delta$BCM vuông tại C, ta có:

Nhận xét rằng $\Delta$AMH và $\Delta$CMB là hai tam giác vuông có $\widehat{AMH}$ = $\widehat{CMB}$ nên chúng đồng dạng, suy ra:

Thay (2) và SA = 2a vào (1), ta được:

Từ hệ thức (1) với SA = 2a không đổi, ta có nhận xét:

• SH đạt giá trị lớn nhất khi:

$AH_{Max}$ ⇔ $AM_{Max}$ ⇔ M $\equiv$ C ⇔ x = a$\sqrt{3}$.

• SH đạt giá trị nhỏ nhất khi:

$AH_{Min}$ ⇔ $AM_{Min}$ ⇔ M $\equiv$ A ⇔ x = 0.

BÀI TẬP ĐỀ NGHỊ

Bài 1. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông đường cao AB = a, BC = 2a, SA = a và vuông góc với mặt phẳng (ABCD). Ngoài ra còn có SC vuông góc với BD.

a. Chứng minh rằng $\Delta$SBC vuông.

b. Tính độ dài AD.

c. Gọi M là một điểm trên đoạn SA, đặt AM = x, với 0 $\leq$ x $\leq$ a. Tính khoảng cách từ D đến BM theo a và x. Tìm các giá trị của x để khoảng cách này có giá trị nhỏ nhất, lớn nhất.

Bài 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O, SA = a và vuông góc với mặt phẳng (ABCD). Gọi M là điểm di động trên đoạn CD, đặt CM = x. Gọi K là hình chiếu vuông góc của S trên BM.

a. Tính độ dài đoạn SK theo a và x.

b. Tìm tập hợp các điểm K thoả mãn tính chất trên.

Bài 3. Cho $\Delta$ABC có BC = a, AC = b, AB = c. Trên đường thẳng vuông góc với (ABC) tại A lấy điểm S sao cho SA = d. Tính khoảng cách từ S đến đường thẳng BC.

Bài 4. Cho mặt phẳng $\alpha$ và một điểm O ngoài $\alpha$, A là một điểm cố định thuộc $\alpha$ sao cho OA không vuông góc với $\alpha$, d là đường thẳng di động trong $\alpha$ nhưng luôn đi qua A. Gọi M là hình chiếu vuông góc của O trên d.

a. Tìm tập hợp các điểm M thoả mãn tính chất trên.

b. Tìm vị trí của d để độ dài OM là lớn nhất.

Bài toán 2: Khoảng cách từ một điểm tới một mặt phẳng.

PHƯƠNG PHÁP CHUNG

Để tính khoảng cách từ điểm O tới mặt phẳng $\alpha$, ta thực hiện theo các bước sau:

Bước 1: Để dựng OH với H là hình chiếu vuông góc của O lên $\alpha$, ta thực hiện:

• Lấy đường thẳng a nằm trong $\alpha$.

• Dựng mặt phẳng (P) qua O vuông góc với a cắt $\alpha$ theo giao tuyến b (cần chọn a sao cho mặt phẳng (P) dễ dựng).

• Trong (P), hạ OH $\perp$ b tại H.

Bước 2: Dựng AH $\perp$ c tại H, khi đó OH là khoảng cách từ O đến $\alpha$.

Bước 3: Tính độ dài của đoạn OH là khoảng cách từ A đến $\alpha$.

Chú ý:

1. Trong bước 1, trước khi chọn a và dụng mặt phẳng (P) nên xét xem a và (P) đã có sẵn trên hình vẽ chưa. Nếu có, chúng ta sẽ giảm thiểu được phép dựng hình.

2. Nếu đã có sẵn đường thẳng d vuông góc với $\alpha$ thì chỉ cần dựng Ox // d ta được Ox $\perp$ $\alpha$

3. Nếu OA // $\alpha$ thì:

d(O, $\alpha$) = d(A, $\alpha$).

4. Nếu OA cắt $\alpha$ tại I thì:

5. Sử dụng tính chất của trục đường tròn, cụ thể:

Định nghĩa: Đường vuông góc với mặt phẳng chứa đường tròn tại tâm của đường tròn gọi là trục của đường tròn đó.

Ta có thể dùng tính chất của trục đường tròn để:

a. Chứng minh đường thẳng vuông góc với mặt phẳng

b. Tính khoảng cách từ một điểm đến một mặt phẳng.

Cụ thể với trường hợp:

• Nếu O là tâm đường tròn ngoại tiếp $\Delta$ABC và M là một điểm cách đều ba điểm A, B, C thì đường thẳng MO là trục của đường tròn ngoại tiếp $\Delta$ABC. Khi đó MO $\perp$ (ABC) và MO = d(M, (ABC)).

• Nếu MA = MB = MC và NA = NB = NC trong đó A, B, C là ba điểm không thẳng hàng thì đường thẳng MN là trục của đường tròn qua ba điểm A, B, C. Khi đó MN $\perp$ (ABC) tại tâm O của đường tròn qua ba điểm A, B, C.

Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SA = a$\sqrt{3}$ và vuông góc với mặt phẳng (ABCD).

a. Hãy dựng đường thẳng qua trung điểm của cạnh SC và vuông góc với mặt phẳng (ABCD).

b. Hãy dựng đường thẳng qua A và vuông góc với mặt phẳng (SBC). Tính khoảng cách từ A đến mặt phẳng (SBC).

c. Tính khoảng cách từ O đến (SBC).

d. Tính khoảng cách từ trọng tâm của $\Delta$SAB đến (SAC).

Giải

a. Gọi M là trung điểm của SC.

Trong $\Delta$SAC, ta có:

OM là đường trung bình

⇒ OM // SA ⇒ OM $\perp$ (ABCD).

Vậy OM là đường thẳng cần dựng.

b. Nhận xét rằng:

Hạ AH vuông góc với SB, ta có ngay AH $\perp$ (SBC).

Vậy AH là đường thẳng cần dựng.

Trong $\Delta$SAB vuông tại A, ta có:

c. Vì AO $\cap$ (SBC) = C nên:

d.

Gọi E là trung điểm AB, hạ EF $\perp$ AC, ta được:

do đó EF chính là khoảng cách từ E tới (SAC).

Trong $\Delta$OAB, ta có:

EF là đường trung bình ⇒

Gọi G là trọng tâm $\Delta$ABC, vì EG $\cap$ (SAC) = S nên:

Ví dụ 2: Cho hình chóp S.ABC có $\widehat{ASB}$ = 90°, $\widehat{BSC}$ = 60°, $\widehat{ASC}$ = 120° và SA = SB = SC = a. Gọi I là trung điểm của cạnh AC.

a. Chứng minh rằng SI $\perp$ (ABC).

b. Tính khoảng cách từ S đến mặt phẳng (ABC).

Giải

a. Trong $\Delta$SAB vuông cân tại S, ta có:

AB = SA$\sqrt{2}$ = a$\sqrt{2}$.

Trong $\Delta$SBC cân tại S có $\widehat{BSC}$ = 60° nên là tam giác đều, suy ra BC = a.

Trong $\Delta$SAC cân tại S, ta có:

$\widehat{SAC}$ = 30°,

Nhận xét rằng:

⇔ $\Delta$ABC vuông tại B ⇒ I là tâm đường tròn ngoại tiếp $\Delta$ABC.

Vậy với SA = SB = SC, ta được:

SI $\perp$ (ABC) và d(S, (ABC)) = SI.

b. Trong $\Delta$SAI vuông tại I, ta có:

Vậy, khoảng cách từ S đến mặt phẳng (ABC) bằng $\large \frac{a}{2}$.

BÀI TẬP ĐỀ NGHỊ

Bài 5. Cho mặt phẳng $\alpha$. Một đường thẳng AB cắt $\alpha$ tại điểm O sao cho O là trung điểm của đoạn AB. Chứng minh rằng A và B cách đều $\alpha$.

Bài 6. Cho hình chóp S.ABC có ABC là tam giác cân đỉnh A, AB = a, $\widehat{BAC}$ = $\alpha$, SA = SB = SC = $\large \frac{a\sqrt{2}}{2}$. Tính khoảng cách từ S đến mặt phẳng (ABC). Tìm điều kiện của $\alpha$ để bài toán có nghĩa.

Bài 7. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A với BC = 2a, $\widehat{ABC}$ = 60°. Gọi M là trung điểm của cạnh BC. Biết SA = SC = SM = a$\sqrt{5}$.

a. Tính khoảng cách từ S đến mặt phẳng (ABC).

b. Tính khoảng cách từ S đến AB.

Bài 8. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và AC = 2a, SA = a và vuông góc với mặt phẳng (ABC).

a. Chứng minh rằng (SAB) $\perp$ (SBC)

b. Tính khoảng cách từ A đến mặt phẳng (SBC).

c. Gọi O là trung điểm của AC. Tính khoảng cách từ O đến (SBC).

Bài 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA = a và vuông góc với mặt phẳng (ABCD).

a. Gọi I là trung điểm của SD. Chứng minh rằng AI $\perp$ (SCD).

b. Tính khoảng cách từ trọng tâm $\Delta$SBC đến mặt phẳng (ABCD).

Bài 10. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, SA = a và vuông góc với mặt phẳng (ABCD). Gọi I, M theo thứ tự là trung điểm của cạnh SC, CD

a. Tính khoảng cách từ A đến mặt phẳng (SBD).

b. Tính khoảng cách từ I đến mặt phẳng (SBD).

c. Tính khoảng cách từ A đến mặt phẳng (SBM).

Bài 11. Cho hình thoi ABCD tâm O, cạnh bằng a và AC = a. Từ trung điểm H của cạnh AB dựng SH vuông góc với mặt phẳng (ABCD) với SH = a.

a. Hãy dựng đường thẳng qua H vuông góc với mặt phẳng (SCD) và tính khoảng cách từ H đến mặt phẳng (SCD).

b. Tính khoảng cách từ O đến mặt phẳng (SCD).

c. Tính khoảng cách từ A đến mặt phẳng (SBC).

Bài 12. Cho $\Delta$ABC cân đỉnh A có $\widehat{A}$ = 120°, cạnh BC = a$\sqrt{3}$. Lấy điểm S ở ngoài mặt phẳng chứa tam giác sao cho SA = a. Tính khoảng cách từ A tới mặt phẳng (SBC).

Bài 13. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA = a và vuông góc với mặt phẳng (ABCD).

a. Tìm trên mặt phẳng (ABCD) một điểm cách đều ba điểm S, B, C và tính khoảng cách chung ấy và khoảng cách từ điểm đó đến mặt phẳng (SBC).

b. Tìm trên mặt phẳng (SBC) một điểm cách đều ba điểm B, C, M với M là trung điểm của cạnh CD. Tính khoảng cách chung ấy.

Bài 14. Trong mặt phẳng $\alpha$ cho $\Delta$ABC vuông tại A có BC = 2a, $\widehat{ACB}$ = 60°. Dựng hai đoạn BB' = a, CC' = 2a cùng vuông góc với $\alpha$ và ở cùng một bên đối với $\alpha$. Tính khoảng cách từ:

a. C' đến mặt phẳng (ABB').

b. Trung điểm của B'C đến mặt phẳng (ACC').

c. B' đến mặt phẳng (ABC').

d. Trung điểm của BC đến mặt phẳng (AB'C').

Bài toán 3: Khoảng cách giữa đường thẳng và mặt phẳng song song. Khoảng cách giữa hai mặt phẳng song song.

PHƯƠNG PHÁP CHUNG

1. Cho đường thẳng d song song với mặt phẳng $\alpha$, để tính khoảng cách giữa d và $\alpha$ ta thực hiện theo các bước:

Bước 1: Chọn một điểm A trên d, sao cho khoảng cách từ A đến $\alpha$ có thể được xác định dễ nhất.

Bước 2: Kết luận d(d, $\alpha$) = d(A, $\alpha$).

2. Cho hai mặt phẳng song song $\alpha$ và $\beta$, để tính khoảng cách giữa $\alpha$ và $\beta$ ta thực hiện theo các bước:

Bước 1: Chọn một điểm A trên $\alpha$, sao cho khoảng cách từ A đến $\beta$ có thể được xác định dễ nhất.

Bước 2: Kết luận d($\alpha$, $\beta$) = d(A, $\beta$).

Ví dụ 1: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a, mặt bên (SBC) vuông góc với đáy. Gọi M, N, P theo thứ tự là trung điểm AB, SA, AC

a. Chứng minh rằng (MNP) // (SBC).

b. Tính khoảng cách giữa hai mặt phẳng (MNP) và (SBC).

Giải

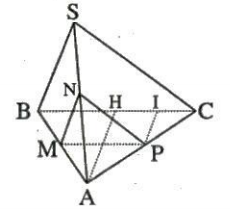
a. Vì M, N, P theo thứ tự là trung điểm AB, SA, AC nên:

MN // SB, do MN là đường trung bình trong $\Delta$SAB

MP // BC, do MP là đường trung bình trong $\Delta$ABC

suy ra (MNP) // (SBC).

b. Từ kết quả câu a), ta có:

d((MNP), (SBC)) = d(P, (SBC)).

Mặt khác ta lại có AP $\cap$ (SBC) = C nên:

Hạ AH vuông góc với BC, ta có ngay AH $\perp$ (SBC). Vậy AH là khoảng cách từ điểm A tới (SBC).

Vì $\Delta$ABC đều có cạnh bằng a nên AH = $\large \frac{a\sqrt{3}}{2}$.

Từ đó, suy ra:

Vậy, khoảng cách giữa hai mặt phẳng (MNP) và (SBC) bằng $\large \frac{a\sqrt{3}}{4}$

Ví dụ 2: Cho hình chóp S.ABCD có SA = $a\sqrt{6}$ và vuông góc với mặt phẳng (ABCD), đáy ABCD là nửa lục giác đều nội tiếp trong đường tròn đường kính AD = 2a.

a. Tính các khoảng cách từ A và B đến mặt phẳng (SCD).

b. Tính khoảng cách từ đường thẳng AD đến mặt phẳng (SBC).

c. Tính diện tích của thiết diện của hình chóp S.ABCD với mặt phẳng $\alpha$ song song với mặt phẳng (SAD) và cách một khoảng bằng $\large \frac{a\sqrt{3}}{4}$

Giải

a. Nhận xét rằng:

Hạ AH vuông góc với SC, ta có ngay AH $\perp$ (SCD).

Vậy AH là khoảng cách từ điểm A tới (SCD).

Trong $\Delta$SAB vuông tại A, ta có:

Gọi I là trung điểm AD, suy ra:

BI // CD ⇒ BI // (SCD) ⇒ d(B, (SCD)) = d(I, (SCD)).

Mặt khác, ta lại có AI $\cap$ (SCD) = D nên:

b. Nhận xét rằng:

AD // CD ⇒ AD // (SBC) = d(AD, (SBC)) = d(A, (SBC)).

Hạ AK vuông góc với BC, ta được:

⇒ BC $\perp$ (SAK) ⇒ (SBC) $\perp$ (SAK) và (SBC) $\cap$ (SAK) = AK.

Hạ AG vuông góc với SK, ta có ngay AG $\perp$ (SBC).

Vậy AG là khoảng cách từ điểm A tới (SBC).

Trong $\Delta$SAK vuông tại A, ta có:

c. Nhận xét rằng:

Giả sử mặt phẳng $\alpha$ song song với mặt phẳng (SAD) cắt AK tại E, khi đó:

⇒ E là trung điểm của AK.

Ta đi xác định thiết diện tạo bởi hình chóp với mặt phẳng $\alpha$ qua E và song song với (SAD), như sau:

và Ex cắt AB, CD theo thứ tự tại M, N là trung điểm của mỗi đoạn.

Trong mặt phẳng (SAB) dựng My // SA và cắt SB tại Q là trung điểm của SB.

Trong mặt phẳng (SCD) dựng Nz // SD và cắt SC tại P là trung điểm của SC.

Vậy, thiết diện tạo bởi hình chóp với mặt phẳng $\alpha$ là MNPQ, ngoài ra vì:

MN // CD // PQ ⇒ MNPQ là hình thang

MQ // SA ⇒ MQ $\perp$(ABCD) ⇒ MQ $\perp$ MN ⇒ MNPQ là hình thang vuông

Từ đó, ta được:

trong đó:

, vì MN là đường trung bình của $\Delta$BCD,

vì PQ là đường trung bình của $\Delta$SBC,

vì MQ là đường trung bình của $\Delta$SAB,

suy ra:

BÀI TẬP ĐỀ NGHỊ

Bài 15. Cho hình hộp chữ nhật $ABCD.A_{1}B_{1}C_{1}D_{1}$ có AB = a, BC = b, $CC_{1}$ = c.

a. Tính khoảng cách từ $AA_{1}$ đến mặt phẳng ($BDD_{1}B_{1}$).

b. Gọi M, N theo thứ tự là trung điểm $AA_{1}$, $BB_{1}$. Tính khoảng cách từ MN đến mặt phẳng ($ABC_{1}D_{1}$).

c. Chứng minh rằng ($AB_{1}D_{1}$) // ($C_{1}BD$). Tính khoảng cách giữa hai mặt phẳng ($AB_{1}D_{1}$) và ($C_{1}BD$).

Bài 16. Cho hình lăng trụ đứng $ABC.A_{1}B_{1}C_{1}$ có $AA_{1}$ = a, đáy ABC là tam giác vuông tại A có BC = 2a, AB = $a\sqrt{3}$

a. Tính khoảng cách từ $AA_{1}$ đến mặt phẳng ($BCC_{1}B_{1}$).

b. Tính khoảng cách từ A đến ($A_{1}BC$).

c. Chứng minh rằng AB vuông góc với mặt phẳng ($ACC_{1}A_{1}$) và tính khoảng cách từ $A_{1}$ đến mặt phẳng ($ABC_{1}$).

d. Gọi M, N, P theo thứ tự là trung điểm của $AA_{1}$, $BB_{1}$, $CC_{1}$. Tính khoảng cách giữa hai mặt phẳng (BMN) và ($A_{1}C_{1}P$).

Bài 17. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = 2a và vuông góc với đáy.

a. Tính khoảng cách từ A đến mặt phẳng (SBC), từ C đến (SBD).

b. M, N lần lượt là trung điểm của AB và AD. Chứng minh rằng MN song song với mặt phẳng (SBD) và tính khoảng cách từ MN đến (SBD).

c. Mặt phẳng $\alpha$ qua BC cắt các cạnh SA, SD theo thứ tự tại E, F. Cho biết AD cách $\alpha$ một khoảng là $\large \frac{a\sqrt{2}}{2}$, tính khoảng cách từ S đến mặt phẳng $\alpha$ và diện tích tứ giác BCFE.

Bài 18. Cho hình chóp S.ABCD có SA = 2a và vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a.

a. Tính các khoảng cách từ A và B đến mặt phẳng (SCD).

b. Tính khoảng cách từ đường thẳng AD đến mặt phẳng (SBC).

c. Tính diện tích của thiết diện của hình chóp S.ABCD với mặt phẳng $\alpha$ song song với mặt phẳng (SAD) và cách một khoảng bằng $\large \frac{a}{3}$

Bài toán 4: Đoạn vuông góc chung của hai đường thẳng chéo nhau.

Khoảng cách giữa hai đường thẳng chéo nhau.

PHƯƠNG PHÁP CHUNG

1. Để dựng đoạn vuông góc chung của hai đường thẳng chéo nhau a và b, ta lựa chọn một trong các cách sau:

Cách 1:

Ta thực hiện theo các bước:

Bước 1: Dựng mặt phẳng $\alpha$ chứa b song song với a.

Bước 2: Chọn M trên a, dựng MH vuông góc với $\alpha$ tại H.

Bước 3: Từ H, dựng đường thẳng $a_{1}$ song song với a, và cắt b tại B.

Bước 4: Từ B, dựng đường thẳng song song với MH, cắt $\alpha$ tại A.

Đoạn AB là đoạn thẳng vuông góc chung của a và b.

Cách 2:

Ta thực hiện theo các bước:

Bước 1: Dựng mặt phẳng $\alpha$ vuông góc với a và tại O.

Bước 2: Dựng hình chiếu vuông góc $b_{1}$ của b trên $\alpha$. Dựng chiếu vuông góc H của O trên $b_{1}$

Bước 3: Từ H, dựng đường thẳng song song với a, cắt b tại B.

Bước 4: Từ B, dựng đường thẳng song song với OH, cắt a tại A. Đoạn AB là đoạn vuông góc chung của a và b.

Cách 3:

(Áp dụng cho trường hợp a $\perp$ b): Ta thực hiện theo các bước:

Bước 1: Dựng mặt phẳng $\alpha$ chứa b, vuông góc với a tại A.

Bước 2: Dựng AB $\perp$ b tại B. Đoạn AB là đoạn vuông góc chung của a và b.

2. Để tính khoảng cách giữa hai đường thẳng chéo nhau, ta lựa chọn một trong các cách sau:

Cách 1: Tính độ dài đoạn vuông góc chung (nếu có).

Cách 2: Tính d(a, $\alpha$) với $\alpha$ là mặt phẳng chứa b song song với a.

Ví dụ 1: Cho hình chóp S.ABCD có đáy là ABCD là hình vuông tâm O cạnh bằng a, SA = a và vuông góc với (ABCD). Tính khoảng cách giữa hai đường thẳng:

a. SB và AD.

b. SC và BD.

c. SB và CD.

d. SC và AD.

e. SB và AC.

Giải

a. Nhận xét rằng:

AD $\perp$ AB, vì ABCD là hình vuông

AD $\perp$ SA, vì SA vuông góc với (ABCD)

suy ra AD $\perp$ (SAB).

Dựng AM vuông góc với SB thì AM là đoạn vuông góc chung của SB và AD.

Trong $\Delta$SAB vuông cân tại A, ta có:

Vậy, khoảng cách giữa SB và AD bằng $\large \frac{a\sqrt{2}}{2}$

b. Nhận xét rằng:

BD $\perp$ AC, vì ABCD là hình vuông

BD $\perp$ SA, vì SA vuông góc với (ABCD)

suy ra BD $\perp$ (SAC).

Dựng OH vuông góc với SC thì OH là đoạn vuông góc chung của SC và BD.

Nhận xét rằng $\Delta$HCO và $\Delta$ACS là hai tam giác vuông có chung góc nhọn $\widehat{C}$ nên chúng đồng dạng, suy ra:

trong đó:

suy ra:

Vậy, khoảng cách giữa SC và BD bằng $\large \frac{a\sqrt{6}}{6}$

c. Nhận xét rằng:

CD // AB ⇒ CD // (SAB)

⇒ d(CD, SB) = d(CD, (SAB)) = d(D, (SAB)) = DA = a.

Vậy, khoảng cách giữa SB và CD bằng a.

d. Nhận xét rằng:

AD // BC ⇒ AD // (SBC)

⇒ d(AD, SC) = d(AD, (SBC) = d(A, (SBC)) = AM = $\large \frac{a\sqrt{2}}{2}$

Vậy, khoảng cách giữa SC và AD bằng $\large \frac{a\sqrt{2}}{2}$

e. Dựng:

Bx // AC ⇒ AC // (S, Bx) ⇒ d(AC, SB) = d(A, (S, Bx))

Hạ AE vuông góc với Bx, ta được:

Hạ AF vuông góc với SE, ta có ngay AE $\perp$ (S, Bx).

Vậy AF là khoảng cách từ điểm A tới (S, Bx).

Trong $\Delta$SAE vuông tại A, ta có:

Vậy, khoảng cách giữa SB và AC bằng $\large \frac{a\sqrt{3}}{3}$

Ví dụ 2: Cho hình chóp S.ABC có SA = 2a và vuông góc với mặt phẳng (ABC), đáy ABC là tam giác vuông cân tại B với AB = a. Gọi M là trung điểm của AC.

a. Hãy dựng đoạn vuông góc chung của SM và BC.

b. Tính độ dài đoạn vuông góc chung của SM và BC.

Giải

a. Để dựng đoạn vuông góc chung của SM và BC ta có thể lựa chọn một trong hai cách trình bày sau:

Cách 1: Gọi N là trung điểm AB, suy ra:

BC // MN ⇒ BC // (SMN).

Ta có:

Hạ BH $\perp$ SN suy ra BH $\perp$ (SMN).

Từ H dựng Hx song song với BC và cắt SM tại E.

Từ E dựng Ey song song với BH và cắt BC tại F.

Đoạn EF là đoạn vuông góc chung của SM và BC.

Cách 2: Nhận xét rằng:

Do đó (SAB) chính là mặt phẳng qua B thuộc BC và vuông góc với BC.

Gọi N là trung điểm AB, suy ra:

MN // BC ⇒ MN $\perp$ (SAB)

suy ra SN là hình chiếu vuông góc của SM trên (SAB).

Hạ BH $\perp$ SN suy ra BH $\perp$ (SMN).

Từ H dựng Hx song song với BC và cắt SM tại E.

Từ E dựng Ey song song với BH và cắt BC tại F.

Đoạn EF là đoạn vuông góc chung của SM và BC.

b. Nhận xét rằng $\Delta$SAN và $\Delta$BHN là hai tam giác vuông có hai góc nhọn đối đỉnh nên chúng đồng dạng, suy ra:

trong đó:

suy ra:

Vậy, khoảng cách giữa SM và BC bằng

Ví dụ 3: Cho hình chóp S.ABCD có đáy là ABCD là hình thoi tâm O, cạnh a, góc $\widehat{A}$ = 60° và có đường cao SO = a.

a. Tính khoảng cách từ O đến (SBC).

b. Tính khoảng cách giữa hai đường thẳng AD và SB.

Giải

a. Hạ OI vuông góc với BC và kéo dài OI cắt AD tại J.

Ta có:

Hạ OH vuông góc với SI, ta có ngay OH $\perp$ (SBC).

Vậy OH là khoảng cách từ điểm O tới (SBC).

Với hình thoi ABCD, ta có:

BD = a, vì $\Delta$ABD đều ⇒ OB = $\large \frac{a}{2}$

Trong $\Delta$OBC vuông tại O, ta có:

Trong $\Delta$SAE vuông tại A, ta có:

Vậy, khoảng cách từ O đến (SBC) bằng $\large \frac{a\sqrt{3}}{4}$

b. Nhận xét rằng:

AD // BC ⇒ AD // (SBC)

⇒ d(AD, SB) = d(AD, (SBC)) = d(J, (SBC)).

Mặt khác, ta lại có JO $\cap$ (SBC) = I nên:

Vậy, khoảng cách giữa SB và AD bằng $\large \frac{a\sqrt{3}}{2}$

Ví dụ 4: Cho đường tròn đường kính AB = 2R chứa trong mặt phẳng $\alpha$, SA vuông góc với mặt phẳng $\alpha$ và SA = h, với 0 < h < 2R. Gọi M là một điểm di động trên đường tròn. Xác định vị trí của M để đoạn nối trung điểm hai đoạn AM và SB là đoạn thẳng vuông góc chung của chúng, khi đó tính độ dài của đoạn vuông góc chung này.

Giải

Gọi E, F theo thứ tự là trung điểm của AM và SB.

Nhận xét rằng, dựa trên tính chất đường trung tuyến trong tam giác vuông, ta có:

⇒ MF = AF ⇔ $\Delta$AFM cân tại F

⇒ EF $\perp$ AM.

Như vậy, để EF là đoạn thẳng vuông góc chung của AM và SB điều kiện là:

EF $\perp$ SB ⇔ $\Delta$ESB cân tại E (1)

⇔ SE = BE.

Đặt AE = x, suy ra ME = x.

Trong $\Delta$SAE vuông tại A, ta có:

Trong $\Delta$EMB vuông tại M, ta có:

Thay (2), (3) vào (1), ta được:

Trong $\Delta$MEF vuông tại E, ta có:

Vậy, với điểm M thuộc đường tròn sao cho thì EF là đoạn thẳng vuông góc chung của AM và SB, và khi đó

BÀI TẬP ĐỀ NGHỊ

Bài 19. Cho hai tam giác cân ABC và ABD có đáy chung AB và không cùng nằm trên một mặt phẳng.

a. Chứng minh rằng AB $\perp$ CD.

b. Xác định rõ đoạn thẳng vuông góc chung của AB và CD.

Bài 20. Cho tứ diện ABCD có ABC là tam giác đều cạnh a, AD vuông góc với BC, AD = a và khoảng cách từ D đến BC là a. Gọi H là trung điểm của BC, I là trung điểm của AH.

a. Chứng minh rằng BC $\perp$ (ADH) và DH = a.

b. Chứng minh rằng DI $\perp$ (ABC).

c. Hãy dựng và tính độ dài đoạn vuông góc chung của AD và BC.

Bài 21. Cho hình chóp S.ABC có SA = 2a và vuông góc với mặt phẳng (ABC), đáy ABC là tam giác vuông tại B với AB = a. Gọi M là trung điểm của AB. Hãy dựng và tính độ dài đoạn vuông góc chung của SM và BC.

Bài 22. Cho tứ diện OABC, trong đó OA, OB, OC đôi một vuông góc và OA = OB = OC = a. Gọi I là trung điểm của BC. Hãy dựng và tính độ dài đoạn vuông góc chung của các cặp đường thẳng:

a. OA và BC.

b. AI và OC.

Bài 23. Cho hình vuông ABCD cạnh bằng a, I là trung điểm của AB. Dựng IS vuông góc với mặt phẳng (ABCD) và IS = $\large \frac{a\sqrt{3}}{2}$. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, SD, SB. Hãy dựng và tính độ dài đoạn vuông góc chung của các cặp đường thẳng:

a. AB và SD.

b. SA và BD.

c. NP và AC.

d. MN và AP.

Bài 24. Cho hình lăng trụ đứng $ABC.A_{1}B_{1}C_{1}$ có đáy là tam giác đều và $AA_{1}$ = h. Biết khoảng cách giữa $A_{1}B_{1}$ và $BC_{1}$ là d. Tính cạnh đáy của lăng trụ theo d và h.

Bài 25. Cho lăng trụ $ABC.A_{1}B_{1}C_{1}$ có các mặt bên đều là hình vuông cạnh a. Gọi D, E, F lần lượt là trung điểm các cạnh BC, $A_{1}C_{1}$, $C_{1}D_{1}$. Hãy dựng và tính độ dài đoạn vuông góc chung của các cặp đường thẳng:

a. $A_{1}B$ và $B_{1}C$

b. DE và $AB_{1}$.

c. $A_{1}B$ và $B_{1}C_{1}$.

d. DE và $A_{1}F$.

Bài 26. Cho hình lăng trụ đứng $ABC.A_{1}B_{1}C_{1}$ có đáy là tam giác đều cạnh a và $AA_{1}$ = $\large \frac{a\sqrt{2}}{2}$. Gọi O, $O_{1}$ theo thứ tự là trung điểm của AB và $A_{1}B_{1}$.

a. Chứng minh rằng AB $\perp$ ($COO_{1}$).

b. Tính khoảng cách giữa hai đường thẳng AB và $B_{1}C$.

Bài 27. Cho tứ diện ABCD có hai mặt ABC và ACD nằm trong hai mặt phẳng vuông góc với nhau, $\Delta$ABC vuông tại A, $\Delta$ACD vuông tại D.

a. Chứng minh rằng các tam giác ABD và BCD đều vuông.

b. Gọi I, J theo thứ tự là trung điểm của AD và BC. Tìm điều kiện để IJ là đoạn vuông góc chung của hai đường thẳng AD và BC.

Bài 28. Cho tứ diện ABCD có bốn mặt là bốn tam giác có diện tích bằng nhau. Chứng minh rằng đoạn nối trung điểm hai cạnh đối diện của tứ diện cũng là đoạn vuông góc chung của hai cạnh đó