§5. HAI MẶT PHẲNG SONG SONG

A. TÓM TẮT LÍ THUYẾT

1. ĐỊNH NGHĨA

Hai mặt phẳng gọi là song song với nhau nếu chúng không có điểm chung.

2. CÁC TÍNH CHẤT

Định lí 1:

Nếu hai mặt phẳng $\alpha$ và $\beta$ song song với nhau thì mọi đường thẳng a nằm trong $\alpha$ đều song song với $\beta$.

Tức là:

Định lí 2:

Nếu một mặt phẳng chứa hai đường thẳng cắt nhau và hai đường thằng này cùng song song với một mặt phẳng cho trước thì hai mặt phẳng đó song song với nhau.

Tức là:

Hệ quả 1:

Nếu một mặt phẳng chứa hai đường thẳng cắt nhau lần lượt song song với hai đường thẳng của một mặt phẳng khác thì hai mặt phẳng đó song song với nhau.

Tức là:

Định lí 3: Qua một điểm O bất kỳ nằm ngoài mặt phẳng $\alpha$ bao giờ cũng dựng được một và chỉ một mặt phẳng song song với mặt phẳng $\alpha$.

Tức là:

Cách dựng:

• Trong $\alpha$ dựng a, b cắt nhau.

• Qua O dựng $a_{1}$ // a, $b_{1}$ // b.

• Mặt phẳng ($a_{1}$, $b_{1}$) là mặt phẳng qua O và song song với $\alpha$.

Hệ quả 2:

Nếu đường thẳng a song song với mặt phẳng $\alpha$ thì qua a có một và chỉ một mặt phẳng $\beta$ song song với mặt phẳng $\alpha$.

Hệ quả 3:

Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.

Tức là:

Hệ quả 4: Nếu từ một điểm A nằm ngoài mặt phẳng $\alpha$ ta dựng một đường thẳng song song với $\alpha$ thì đường thẳng này nằm trong mặt phẳng qua A và song song với $\alpha$.

Tức là:

Định lí 4:

Nếu hai mặt phẳng song song bị cắt bởi một mặt phẳng thứ ba thì hai giao tuyến song song với nhau.

Tức là:

Định lí 5:

Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau.

Tức là:

Định lí 6: (Định lí Talét trong không gian)

Ba mặt phẳng song song chắn trên hai cát tuyến bất kỳ những đoạn thẳng tương ứng tỷ lệ.

Tức là:

B. PHƯƠNG PHÁP GIẢI TOÁN

Bài toán 1: Chứng minh hai mặt phẳng song song.

PHƯƠNG PHÁP CHUNG

Để chứng minh 2 mặt phẳng song song ta đi chứng minh mặt phẳng này chứa hai đường thẳng cắt nhau song song với mặt phẳng kia (hoặc song song với hai đường thẳng cắt nhau nằm trong mặt phẳng kia).

Chú ý:

1. Sử dụng tính chất:

ta được thêm một phương pháp để chứng minh đường thẳng a song song với $\alpha$.

2. Sử dụng định lí Ta – lét đảo ta được thêm một phương pháp để chứng minh đường thẳng song song với mặt phẳng, cụ thể:

Ba điểm $A_{1}$, $B_{1}$, $C_{1}$ thuộc đường thẳng a và ba điểm $A_{2}$, $B_{2}$, $C_{2}$ thuộc đường thẳng b (với a và b chéo nhau) thoả mãn:

suy ra tồn tại duy nhất bộ ba mặt phẳng $\alpha$, $\beta$, $\gamma$ song song lần lượt chứa các đoạn thẳng $A_{1}A_{2}$, $B_{1}B_{2}$, $C_{1}C_{2}$, từ đó ta được các kết quả:

$A_{1}A_{2}$ song song với $\beta$ và $\gamma$

$B_{1}B_{2}$ song song với $\alpha$ và $\gamma$.

$C_{1}C_{2}$ song song với $\alpha$ và $\beta$.

Điều quan trọng nhất cần chỉ ra được sự tồn tại của một trong ba mặt phẳng.

Ví dụ 1: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA và CD.

a. Chứng minh rằng mặt phẳng (OMN) và mặt phẳng (SBC) song song với nhau

b. Gọi I là trung điểm SC, J là một điểm trên (ABCD) và cách đều AB và CD. Chứng minh IJ song song với (SAB).

c. Giả sử hai tam giác SAD, ABC đều cân tại A. Gọi AE, AF là các đường phân giác trong của các tam giác ACD và SAB. Chứng minh EF song song với (SAD).

Giải

a. Nhận xét rằng:

b. Gọi P, Q theo thứ tự là trung điểm AD và BC, suy ra J thuộc đường thẳng PQ.

Nhận xét rằng:

c.

Sử dụng tính chất đường phân giác, ta có:

suy ra tồn tại duy nhất bộ ba mặt phẳng song song lần lượt chứa các đoạn thẳng SD, EF, CD và ta thấy ngay một trong ba mặt phẳng đó chính là (SAD), do đó:

EF // (SAD).

Chú ý: Nếu các em học sinh cảm thấy khó hiểu trong lời giải của câu c) thì có thể sử dụng lời giải tường minh hơn như sau:

Dựng EH // SD, H $\in$ SC. (1)

Nhận xét rằng:

Từ (1) và (2) suy ra:

(HEF) // (SAD) ⇒ EF // (SAD).

Ví dụ tiếp theo sẽ sử dụng lại cách trình bày này để giúp các em học sinh nắm vững hơn.

Ví dụ 2: Cho hai hình vuông ABCD và ABEF ở trong 2 mặt phẳng khác nhau. Trên các đường chéo AC và BF lần lượt lấy các điểm M, N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M, N lần lượt cắt AD, AF tại M', N'.

a. Chứng minh răng (CBE) song song với (ADF).

b. Chứng minh rằng (DEF) song song với (MNN'M').

c. Gọi I là trung điểm của MN, tìm tập hợp điểm I khi M, N di động.

Giải

a. Ta có nhận xét:

b. Ta có nhận xét:

⇒ M'N' // DF. (1)

Mặt khác, ta có MM' // CD. (2)

Từ (1) và (2) suy ra:

(MNN'M') // (DEF).

c. I chạy trên trung tuyến của $\Delta$ADE kẻ từ A.

Ví dụ 3: Cho tứ diện ABCD. Gọi I, J là hai điểm di động lần lượt trên các cạnh AD, BC sao cho luôn có

a. Chứng minh rằng IJ luôn song song với một mặt phẳng cố định.

b. Tìm tập hợp điểm M chia đoạn IJ theo tỉ số k cho trước (tức điểm M thoả $\overrightarrow{IM}$ = k. $\overrightarrow{MJ}$).

Giải

a. Dựng JH // AB, H $\in$ AC. (1)

Nhận xét rằng:

Gọi $\alpha$ là mặt phẳng chứa AB và song song với CD, suy ra $\alpha$ là mặt phẳng cố định và (HIJ) // $\alpha$

b. Giải sử (HIJ) cắt BD tại K, dễ thấy HIKJ là hình bình hành. Qua M kẻ PQ song song với AB (P $\in$ HI và Q $\in$ JK). Ta có:

AP $\cap$ BQ = E và EM $\cap$ AB = F.

Nhận xét rằng:

⇒ E là điểm chia CD theo tỉ số k.

⇒ F là điểm chia AB theo tỉ số k

Vậy, tập hợp điểm M chia đoạn IJ theo tỉ số k là đoạn EF với E, F lần lượt là điểm chia CD và AB theo tỉ số k.

BÀI TẬP ĐỀ NGHỊ

Bài 1. Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA, SD.

a. Chứng minh rằng (OMN) song song với (SBD).

b. Gọi P và Q là trung điểm của AB và ON. Chứng minh rằng PQ song song với (SBC).

Bài 2. Cho tứ diện ABCD có AB = AC = AD. Chứng minh rằng các đường phân giác ngoài của các góc $\widehat{BAC}$, $\widehat{CAD}$, $\widehat{DAB}$ đồng phẳng.

Bài 3. Trong mặt phẳng $\alpha$ cho hình bình hành ABCD. Ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với $\alpha$ lần lượt đi qua các điểm A, B, C, D. Mặt phẳng $\beta$ cắt bốn nửa đường thẳng nói trên tại $A_{1}$, $B_{1}$, $C_{1}$, $D_{1}$.

a. Chứng minh rằng ($AA_{1}$, $BB_{1}$) song song với ($CC_{1}$, $DD_{1}$).

b. Chứng minh rằng $A_{1}B_{1}C_{1}D_{1}$ là hình bình hành.

c. Chứng minh rằng $AA_{1}$ + $CC_{1}$ = $BB_{1}$ + $DD_{1}$.

Bài 4. Cho hai nửa đường thẳng chéo nhau Ax, By, M và N là 2 điểm di động lần lượt trên Ax, By sao cho AM = BN. Vẽ $\overrightarrow{NP}$ = $\overrightarrow{BA}$.

a. Chứng minh MP có phương không đổi và MN luôn song song với một mặt phẳng cố định.

b. Gọi I là trung điểm của MN. Chứng minh rằng I nằm trên một đường thẳng cố định khi M, N di động.

Bài 5. Cho hai đường thẳng chéo nhau a và b. Tìm tập hợp các điểm I trên đoạn thẳng MN và chia MN theo tỉ số k cho trước khi M, N di động lần lượt trên a, b.

Bài toán 2: Tìm giao tuyến của hai mặt phẳng.

Thiết diện song song với một mặt phẳng cho trước.

PHƯƠNG PHÁP CHUNG

1. Ta sử dụng thêm định lí 4 để xác định giao tuyến của hai mặt phẳng.

2. Thiết diện của hình chóp cắt bởi một mặt phẳng song song với một mặt phẳng cho trước được xác định thông qua việc tìm được các đoạn giao tuyến như trên.

Ví dụ 1: Cho tứ diện ABCD. Gọi M là trung điểm của AB. Hỏi mặt phẳng (P) qua điểm M, song song với cả AD và BC có đi qua trung điểm N của CD không ? Tại sao ?

Giải

Mặt phẳng (P) có đi qua trung điểm N của CD, bởi:

• Mặt phẳng (Q) chứa AD và song song với BC.

• Mặt phẳng (R) chứa BC và song song với AD.

Khi đó, ba mặt phẳng (P), (Q), (R) song song với nhau sẽ chắn trên hai cát tuyến AB và CD các đoạn thẳng tương ứng tỉ lệ, cụ thể:

⇒ DN = CN ⇒ N là trung điểm CD.

Ví dụ 2: Cho hai mặt phẳng song song $\alpha$ và $\beta$. A, B, C là ba điểm không thẳng hàng thuộc $\alpha$ và MN là đoạn thẳng nằm trong $\beta$.

a. Tìm giao tuyến của (MAB) và $\beta$; giao tuyến của (NAC) và $\beta$.

b. Tìm giao tuyến của (MAB) và (NAC).

Giải

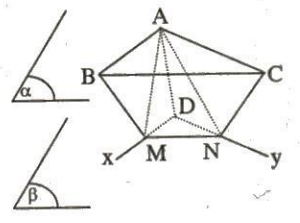
a. Ta có:

Ta có:

b. Vì AB cắt AC tại A nên

Mx $\cap$ Ny = D ⇒ (MAB) $\cap$ (NAC) = AD.

Ví dụ 3: Cho hình chóp S.ABCD đáy ABCD là hình bình hành tâm O có AC = a, BD = b. Tam giác SBD là tam giác đều. Một mặt phẳng $\alpha$ di động song song với (SBD) và qua điểm I trên đoạn AC.

a. Xác định thiết diện của hình chóp với mặt phẳng $\alpha$.

b. Tính diện tích thiết diện theo a, b và AI = x.

Giải

Bạn đọc tự vẽ hình.

a. Ta xét hai trường hợp:

Trường hợp 1: Nếu I $\in$ OA thì:

⇒ Ix // BD và Ix cắt AB, AD theo thứ tự M và N.

Lập luận tương tự ta cũng có:

• $\alpha$ cắt mặt phẳng (SAB) theo đoạn giao tuyến MP song song với SB.

• $\alpha$ cắt mặt phẳng (SAD) theo đoạn giao tuyến NP song song với SD.

Trường hợp 2: Nếu I $\in$ OC thì:

⇒ Ix // BD và Ix cắt CB, CD theo thứ tự H và L

Lập luận tương tự ta cũng có:

• $\alpha$ cắt mặt phẳng (SBC) theo đoạn giao tuyến HK song song với SB.

• $\alpha$ cắt mặt phẳng (SCD) theo đoạn giao tuyến LK song song với SD.

b. Trước tiên, ta có ngay:

Ta lần lượt xét hai trường hợp của thiết diện:

Trường hợp 1: Nếu I $\in$ OA thì 0 < x < $\large \frac{a}{2}$.

Ta có:

Trường hợp 2: Nếu I $\in$ OC thì $\large \frac{a}{2}$ < x < a.

Ta có:

Tóm lại, ta có:

Ví dụ 4: Cho hình chóp S.ABCD đáy ABCD là hình thang, đáy lớn AB = 3a, AD = CD = a. Mặt bên (SAB) là tam giác cân đỉnh S với SA = 2a, $\alpha$ là mặt phẳng di động song song với (SAB), cắt các cạnh AD, BC, SC, SD theo thứ tự tại M, N, P, Q.

a. Chứng minh MNPQ là hình thang cân.

b. Đặt x = AM, với 0 < x < a. Định x để MNPQ ngoại tiếp được một đường tròn. Tính bán kính đường tròn đó.

c. Gọi I là giao điểm của MQ và NP. Tìm tập hợp những điểm I khi M di động trên AD.

d. Gọi J là giao điểm của MP và NQ. Chứng minh IJ có phương không đổi và J di động trong một mặt phẳng cố định.

Giải

a. Ta lần lượt có:

Lập luận tương tự ta cũng có:

NP // BS, PQ // CD, QM // SA.

Nhận xét rằng:

MN // PQ bởi AB // CD.

Vậy, thiết diện MNPQ là hình thang cân.

b. Để MNPQ ngoại tiếp được một đường tròn điều kiện là:

MN + PQ = MQ + NP ⇔ MN + PQ = 2MQ. (1)

Trong $\Delta$SAD, ta có:

(2)

Trong $\Delta$SCD, ta có:

Giả sử AB cắt CD tại O và OD = y, ta có:

Vậy, với x = $\large \frac{a}{3}$ thì MNPQ ngoại tiếp được một đường tròn.

Khi đó, xét hình thang cân MNPQ, hạ đường cao QH, ta có:

suy ra bán kính đường tròn nội tiếp MNPQ là r = $\large \frac{1}{2}$QH = $\large \frac{a\sqrt{7}}{6}$

Câu c) và d) học sinh tự làm:

BÀI TẬP ĐỀ NGHỊ

Bài 6. Cho hai đường thẳng chéo nhau a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q). Chứng minh rằng nếu điểm M không nằm trên (P) và không nằm trên (Q) thì có duy nhất một đường thẳng đi qua M cắt cả a và b.

Bài 7. Cho hai đường thẳng chéo nhau. Chứng minh rằng có đúng hai mặt phẳng song song với nhau lần lượt đi qua hai đường thẳng đó.

Bài 8. Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại 4 điểm A', B', C', D'. Chứng minh rằng A’B'C'D' là hình bình hành.

Bài 9. Cho hai điểm M, N lần lượt thay đổi trên hai mặt phẳng song song (P) và (Q). Tìm tập hợp các điểm I thuộc đoạn thẳng MN sao cho $\large \frac{IM}{IN}$ = k, k $\neq$ 0 cho trước.

Bài 10. Cho hình chóp S.ABCD, đáy ABCD là hình thang có các cạnh đáy AB, CD với CD = p.AB (0 < p < 1). $S_{0}$ là diện tích tam giác SAB. $\alpha$ là mặt phẳng qua điểm M trên cạnh AD và song song với mặt phẳng (SAB). Đặt $\large \frac{DM}{AD}$ = x, với 0 < x < 1.

a. Xác định thiết diện của hình chóp S.ABCD với mặt phẳng $\alpha$. Tính diện tích thiết diện theo $S_{0}$, p, x.

b. Tính x để diện tích thiết diện bằng một nửa diện tích tam giác SAB.

Bài 11. Cho tứ diện ABCD, gọi $G_{1}$, $G_{2}$, $G_{3}$ lần lượt là trọng tâm các tam giác ABC, ACD, ADB.

a. Chứng minh mặt phẳng ($G_{1}G_{2}G_{3}$) song song với mặt phẳng (BCD).

b. Tìm thiết diện của tứ diện ABCD với mặt phẳng ($G_{1}G_{2}G_{3}$). Tính diện tích thiết diện biết diện tích tam giác BCD là s.

c. M là điểm di động bên trong tứ diện sao cho $G_{1}M$ luôn song song với mặt phẳng (ACD). Tìm tập hợp những điểm M.

Bài 12. Cho hình chóp S.ABCD, một mặt phẳng $\alpha$ di động luôn luôn song song với (ABC), cắt SA, SB, SC lần lượt tại $A_{1}$, $B_{1}$, $C_{1}$. Tìm tập hợp điểm chung của 3 mặt phẳng (A'BC), (B'CA), (C'AB).

Bài 13. Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Một mặt phẳng $\alpha$ cắt SA, SB, SC, SD lần lượt tại A', B', C', D'. Chứng minh rằng điều kiện cần và đủ để A'B'C'D' là hình bình hành là $\alpha$ song song với (ABCD).

Bài 14. Cho hình chóp S.ABCD. Tứ giác đáy có AB và CD cắt nhau tại E, AD và BC cắt nhau tại F, AC và BC cắt nhau tại G. $\alpha$ là mặt phẳng cắt SA, SB, SC lần lượt tại A', B', C'.

a. Tìm giao điểm D' của SD với $\alpha$.

b. Tìm điều kiện của $\alpha$ để A'B' // C'D'.

c. Với điều kiện nào của $\alpha$ thì A'B'C'D' là hình bình hành? Chứng minh rằng khi đó

Bài 15. Cho mặt phẳng $\alpha$ và 2 đường thẳng chéo nhau $d_{1}$, $d_{2}$ cắt $\alpha$ tại A, B. ($\Delta$) là đường thẳng thay đổi luôn luôn song song với $\alpha$, cắt $d_{1}$ tại M, $d_{2}$ tại N. Đường thẳng qua N và song song với $d_{1}$ cắt $\alpha$ tại N'.

a. Tứ giác AMNN' là hình gì ? tìm tập hợp điểm N'.

b. Xác định vị trí của ($\Delta$) để MN có độ dài nhỏ nhất.

c. Gọi O là trung điểm của AB, I là trung điểm của MN. Chứng minh OI là đường thẳng cố định khi M di động.

d. $\Delta$BMN vuông cân tại B và BM = a. Tính diện tích thiết diện của hình chóp B.AMNN’ với mặt phẳng qua O và song song mặt phẳng (BMN).