CHƯƠNG III : VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC
§1. VECTƠ TRONG KHÔNG GIAN. SỰ ĐỒNG PHẲNG CỦA CÁC VECTƠ
A. TÓM TẮT LÍ THUYẾT
1. VECTƠ TRONG KHÔNG GIAN
Vectơ, các phép toán vectơ trong không gian được định nghĩa hoàn toàn giống như trong mặt phẳng, chúng có các tính chất đã biết.
Quy tắc hình hộp: Cho hình hộp $ABCD.A_{1}B_{1}C_{1}D_{1}$, ta luôn có:
$\overrightarrow{AC_{1}}$ = $\overrightarrow{AB}$ + $\overrightarrow{AD}$ + $\overrightarrow{AA_{1}}$
Trọng tâm của tứ diện: Điểm G là trọng tâm của tứ diện ABCD khi và chỉ khi:
$\overrightarrow{GA}$ + $\overrightarrow{GB}$ + $\overrightarrow{GC}$ + $\overrightarrow{GD}$ = $\vec{0}$.
2. SỰ ĐỒNG PHẲNG CỦA CÁC VECTƠ. ĐIỀU KIỆN ĐỂ BA VECTƠ ĐỒNG PHẲNG
Định nghĩa: Ba vectơ được gọi là đồng phẳng nếu giá của chúng song song với một mặt phẳng.
Định lí 1 (Điều kiện để ba vectơ đồng phẳng): Cho hai vectơ không cùng phương $\vec{a}$ và $\vec{b}$. Khi đó ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ đồng phẳng khi và chỉ khi có các số m, n sao cho $\vec{c}$ = m$\vec{a}$ + n$\vec{b}$. Hơn nữa, các số m, n là duy nhất.
Định lí 2: Nếu ba vectơ $\vec{a}$, $\vec{b}$ và $\vec{c}$ không đồng phẳng thì với vectơ $\vec{d}$ bất kì, ta đều tìm được các số m, n, p sao cho $\vec{d}$ = m$\vec{a}$ + n$\vec{b}$ + p$\vec{c}$. Hơn nữa, các số m, n, p là duy nhất.
B. PHƯƠNG PHÁP GIẢI TOÁN
Bài toán 1: Chứng minh một đẳng thức vectơ.
PHƯƠNG PHÁP CHUNG
Sử dụng:
• Quy tắc ba điểm: Ta có:
$\overrightarrow{AB}$ = $\overrightarrow{AC}$ + $\overrightarrow{CB}$, xen điểm C.
$\overrightarrow{AB}$ - $\overrightarrow{AC}$ = $\overrightarrow{CB}$, hiệu hai vectơ cùng gốc.
• Quy tắc hình bình hành: Với hình bình hành ABCD luôn có:
$\overrightarrow{AC}$ = $\overrightarrow{AB}$ + $\overrightarrow{AD}$.
• Quy tắc hình hộp: Cho hình hộp $ABCD.A_{1}B_{1}C_{1}D_{1}$, ta luôn có:
$\overrightarrow{AC_{1}}$ = $\overrightarrow{AB}$ + $\overrightarrow{AD}$ + $\overrightarrow{AA_{1}}$
• Quy tắc trung điểm: Với điểm M tuỳ ý và I là trung điểm của AB luôn có:
$\overrightarrow{MI}$ = $\large \frac{1}{2}$($\overrightarrow{MA}$ + $\overrightarrow{MB}$)
• Trọng tâm của tam giác: Điểm G là trọng tâm của $\Delta$ABC khi và chỉ khi:
$\overrightarrow{GA}$ + $\overrightarrow{GB}$ + $\overrightarrow{GC}$ = $\vec{0}$.
• Trọng tâm của tứ diện: Điểm G là trọng tâm của tứ diện ABCD khi và chỉ khi:
$\overrightarrow{GA}$ + $\overrightarrow{GB}$ + $\overrightarrow{GC}$ + $\overrightarrow{GD}$ = $\vec{0}$.
• Các tính chất của phép cộng, trừ vectơ và phép nhân một số với một vectơ.
Để thực hiện phép biến đổi tương đương cho đẳng thức cần chứng minh. Và khi đó, ta lựa chọn một trong các hướng biến đổi sau:
Hướng 1: Biến đổi một vế thành vế còn lại (VT ⇒ VP hoặc VP ⇒ VT).
Khi đó:
• Nếu xuất phát từ vế phức tạp ta cần thực hiện việc đơn giản biểu thức.
• Nếu xuất phát từ vế đơn giản ta cần thực hiện việc phân tích vectơ.
Hướng 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
Hướng 3: Biến đổi một đẳng thức vectơ đã biết là luôn đúng thành đẳng thức cần chứng minh.
Hướng 4: Tạo dựng các hình phụ.
Ví dụ 1: Điểm G là trọng tâm của tứ diện ABCD, chứng minh rằng:
$\overrightarrow{MA}$ + $\overrightarrow{MB}$ + $\overrightarrow{MC}$ + $\overrightarrow{MD}$ = 4$\overrightarrow{MG}$, với mọi điểm M.
Giải
.png)
Gọi I và J theo thứ tự là trung điểm của AB và CD, sử dụng quy tắc ba điểm bằng cách xen vào giữa, ta lần lượt có:
$\overrightarrow{MA}$ = $\overrightarrow{MG}$ + $\overrightarrow{GA}$,
$\overrightarrow{MB}$ = $\overrightarrow{MG}$ + $\overrightarrow{GB}$,
$\overrightarrow{MC}$ = $\overrightarrow{MG}$ + $\overrightarrow{GC}$,
$\overrightarrow{MD}$ = $\overrightarrow{MG}$ + $\overrightarrow{GD}$
suy ra: $\overrightarrow{MA}$ + $\overrightarrow{MB}$ + $\overrightarrow{MC}$ + $\overrightarrow{MD}$ = 4$\overrightarrow{MG}$ + ($\overrightarrow{GA}$ + $\overrightarrow{GB}$ + $\overrightarrow{GC}$ + $\overrightarrow{GD}$) = 4$\overrightarrow{MG}$ , đpcm.
Ví dụ 2: Cho hình hộp $ABCD.A_{1}B_{1}C_{1}D_{1}$. Gọi P, R theo thứ tự là trung điểm của AB, $A_{1}D_{1}$, gọi $P_{1}$, Q, $Q_{1}$, $R_{1}$ theo thứ tự là giao điểm của các đường chéo của các mặt ABCD, $CDD_{1}C_{1}$, $A_{1}B_{1}C_{1}D_{1}$, $ADD_{1}A_{1}$:
a. Chứng minh rằng $\overrightarrow{PP_{1}}$ + $\overrightarrow{QQ_{1}}$ + $\overrightarrow{RR_{1}}$ = $\vec{0}$.
b. Chứng minh hai tam giác PQR và $P_{1}Q_{1}R_{1}$ có trọng tâm trùng nhau.
Giải
.png)
a. Ta có:
.png)
suy ra:
.png)
b. Gọi G, $G_{1}$ theo thứ tự là trọng tâm các tam giác PQR và $P_{1}Q_{1}R_{1}$ ta có:
.png)
suy ra:
.png)
BÀI TẬP ĐỀ NGHỊ
Bài 1. Trong không gian, cho hai tam giác ABC và $A_{1}B_{1}C_{1}$ theo thứ tự có các trọng tâm là G và $G_{1}$. Chứng minh rằng:
$\overrightarrow{AA_{1}}$ + $\overrightarrow{BB_{1}}$ + $\overrightarrow{CC_{1}}$ = 3$\overrightarrow{GG_{1}}$
Bài 2. Cho tứ diện ABCD.
a. Gọi I, J theo thứ tự là trung điểm của AC, BD. Chứng minh rằng:
$\overrightarrow{AB}$ + $\overrightarrow{CD}$ = $\overrightarrow{AD}$ + $\overrightarrow{CB}$ = 2$\overrightarrow{IJ}$.
b. Gọi E, F là hai điểm thoả mãn $\overrightarrow{EA}$ = t$\overrightarrow{EB}$, $\overrightarrow{FC}$ = t$\overrightarrow{FD}$, với t $\neq$ 0, 1.
Chứng minh rằng:
$\overrightarrow{AC}$ = t$\overrightarrow{BD}$ + (1 – t)$\overrightarrow{EF}$.
Bài 3. Cho tứ diện ABCD. Gọi E là trọng tâm $\Delta$BCD, I, $I_{1}$, J, $J_{1}$, K, $K_{1}$ theo thứ tự là trung điểm của AB, CD, CA, BD, AD, BC. Điểm G thoả mãn hệ thức:
$\overrightarrow{GA}$ + $\overrightarrow{GB}$ + $\overrightarrow{GC}$ + $\overrightarrow{GD}$ = $\vec{0}$.
Chứng minh rằng:
a. $\overrightarrow{II_{1}}$ + $\overrightarrow{JJ_{1}}$ + $\overrightarrow{KK_{1}}$ = 2$\overrightarrow{AG}$.
b. $\overrightarrow{GA}$ + 3$\overrightarrow{GE}$ = $\vec{0}$.
Bài 4. Cho hành hộp $ABCD.A_{1}B_{1}C_{1}D_{1}$, gọi I là giao điểm của $AC_{1}$ với mặt phẳng ($BDA_{1}$). Chứng minh rằng:
.png)
Bài 5. Cho tứ diện ABCD, lấy các điểm $A_{1}$, $B_{1}$, $C_{1}$, $D_{1}$ theo thứ tự thuộc các cạnh AB, BC, CD, DA. Giả sử tồn tại điểm O sao cho:
.png)
Chứng minh rằng:
.png)
Bài toán 2: Xét tính đồng phẳng, không đồng phẳng của ba vectơ.
PHƯƠNG PHÁP CHUNG
1. Để chứng minh ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ đồng phẳng, ta đi chứng minh tồn tại cặp số thực m, n, sao cho:
$\vec{c}$ = m$\vec{a}$ + n$\vec{b}$. (1)
Chú ý: Trong trường hợp bài toán yêu cầu xác định điều kiện của tham số để ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ đồng phẳng ta sẽ xuất phát từ điều kiện (1).
2. Để chứng minh ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ không đồng phẳng, ta đi chứng minh:
m$\vec{a}$ + n$\vec{b}$ + p$\vec{c}$ = $\vec{0}$ ⇔ m = n = p = 0.
Ví dụ 1: Cho tứ diện ABCD. Gọi M và N theo thứ tự là trung điểm của AB và CD. Chứng minh rằng ba vectơ $\overrightarrow{BC}$, $\overrightarrow{MN}$, $\overrightarrow{AD}$ đồng phẳng.
Giải
.png)
Từ giả thiết, ta có:
.png)
⇒ BC, MN, AD nằm trên ba mặt phẳng song song
⇒ ba vectơ $\overrightarrow{BC}$, $\overrightarrow{MN}$, $\overrightarrow{AD}$ đồng phẳng.
Ví dụ 2: Cho tứ diện OABC. Ba điểm M, N, P trong không gian thoả mãn:
.png)
a. Xác định t để ba vectơ $\overrightarrow{OM}$, $\overrightarrow{ON}$, $\overrightarrow{OP}$ đồng phẳng.
b. Cho t = 0, hãy biểu diễn vectơ $\vec{v}$ = 5$\overrightarrow{OA}$ + 10$\overrightarrow{OB}$ - 15$\overrightarrow{OC}$ theo ba vectơ $\overrightarrow{OM}$, $\overrightarrow{ON}$, $\overrightarrow{OP}$.
Giải
a. Để $\overrightarrow{OM}$, $\overrightarrow{ON}$, $\overrightarrow{OP}$ đồng phẳng điều kiện là tồn tại cặp số thực $\alpha$, $\beta$, sao cho:
.png)
b. Với t = 0, ta được:
.png)
Giải hệ phương trình tạo bởi (1), (2), (3) theo các ẩn $\overrightarrow{OA}$, $\overrightarrow{OB}$, $\overrightarrow{OC}$, ta được:
.png)
BÀI TẬP ĐỀ NGHỊ
Bài 6. Trong không gian, cho ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ khác vectơ không.
a. Nếu $\vec{a}$ – 3$\vec{b}$ – 4$\vec{c}$ = $\vec{0}$ thì ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ có đồng phẳng không ?
b. Giả sử ta có:
$\alpha$$\vec{a}$ + $\beta$$\vec{b}$ + $\gamma$$\vec{c}$ = $\vec{0}$
Với điều kiện nào của $\alpha$, $\beta$, $\gamma$ để ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$
• Đồng phẳng.
• Không đồng phẳng.
Bài 7. Cho tứ diện OABC, đặt:
.png)
Xác định t để ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ đồng phẳng.
Bài 8. Trong không gian, cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng. O là điểm bất kỳ. Chứng minh rằng 4 điểm A, B, C, D đồng phẳng khi và chỉ khi tồn tại bốn số $\alpha$, $\beta$, $\gamma$, $\eta$ sao cho:
.png)
Bài 9. Cho tứ diện OABC, gọi $A_{1}$, $B_{1}$, $C_{1}$, $D_{1}$ là các điểm thuộc AB, BC, CD, DA sao cho:
.png)
a. Chứng minh rằng với điểm O bất kỳ trong không gian ta luôn có:
.png)
b. Xác định giá trị của t để bốn điểm $A_{1}$, $B_{1}$, $C_{1}$, $D_{1}$ đồng phẳng.
Bài toán 3: Biểu diễn một vectơ thành tổ hợp vectơ.
PHƯƠNG PHÁP CHUNG
Ta lựa chọn một trong hai hướng:
Hướng 1: Từ giả thiết xác định được tính chất hình học, rồi từ đó khai triển vectơ cần biểu diễn bằng phương pháp xen điểm hoặc hiệu của hai vectơ cùng gốc.
Hướng 2: Từ giả thiết thiết lập được mối liên hệ vectơ giữa các đối tượng, rồi từ đó khai triển biểu thức này bằng phương pháp xen điểm hoặc hiệu của hai vectơ cùng gốc.
Ví dụ 1: Cho hình chóp SABC. Đáy ABC có trọng tâm G. Hãy phân tích vectơ $\overrightarrow{SA}$ theo ba vectơ $\overrightarrow{SB}$, $\overrightarrow{SG}$, $\overrightarrow{BC}$.
Giải
.png)
Ta có:
$\overrightarrow{SA}$ = $\overrightarrow{SG}$ + $\overrightarrow{GA}$
$\overrightarrow{SB}$ = $\overrightarrow{SG}$ + $\overrightarrow{GB}$
$\overrightarrow{SC}$ = $\overrightarrow{SG}$ + $\overrightarrow{GC}$
suy ra:
.png)
Ví dụ 2: Cho tứ diện ABCD. Gọi $A_{1}$, $B_{1}$, $C_{1}$, $D_{1}$ là các điểm thoả mãn:
.png)
Đặt $\overrightarrow{AB}$ = $\vec{i}$, $\overrightarrow{AC}$ = $\vec{j}$, $\overrightarrow{AD}$ = $\vec{k}$. Hãy biểu diễn các vectơ $\overrightarrow{A_{1}B_{1}}$, $\overrightarrow{A_{1}C_{1}}$, $\overrightarrow{A_{1}D_{1}}$ theo ba vectơ $\vec{i}$, $\vec{j}$, $\vec{k}$.
Giải
.png)
Ta lần lượt có:
.png)
.png)
Từ đó, ta lần lượt có:
.png)
Tổng quát hoá: Cho tứ diện ABCD. Gọi $A_{1}$, $B_{1}$, $C_{1}$, $D_{1}$ là các điểm thoả mãn:
.png)
với t $\neq$ 0, 1. Đặt $\overrightarrow{AB}$ = $\vec{i}$, $\overrightarrow{AC}$ = $\vec{j}$, $\overrightarrow{AD}$ = $\vec{k}$. Hãy biểu diễn các vectơ $\overrightarrow{A_{1}B_{1}}$, $\overrightarrow{A_{1}C_{1}}$, $\overrightarrow{A_{1}D_{1}}$ theo ba vectơ $\vec{i}$, $\vec{j}$, $\vec{k}$.
Bằng phương pháp tương tự như đã trình bày trong lời giải trên, chúng ta sẽ nhận được kết quả:
.png)
BÀI TẬP ĐỀ NGHỊ
Bài 10. Cho tứ diện ABCD, gọi G là trọng tâm $\Delta$ABC, đặt $\overrightarrow{DA}$ = $\vec{i}$, $\overrightarrow{DB}$ = $\vec{j}$, $\overrightarrow{DC}$ = $\vec{k}$. Hãy biểu diễn các vectơ $\overrightarrow{GA}$, $\overrightarrow{GB}$, $\overrightarrow{GC}$ theo ba vectơ $\vec{i}$, $\vec{j}$, $\vec{k}$.
Bài 11. Cho hình lập phương $ABCD.A_{1}B_{1}C_{1}D_{1}$ có tâm O, gọi I là tâm của mặt $CDD_{1}C_{1}$. Hãy phân tích các vectơ $\overrightarrow{AO}$, $\overrightarrow{AI}$ theo ba vectơ $\overrightarrow{AB}$, $\overrightarrow{AD}$, $\overrightarrow{AA_{1}}$
Bài 12. Cho tứ diện vuông OABC, vuông tại O và OA = OB = OC. Điểm M thoả mãn $\mid \overrightarrow{OM}\mid$ = OA, nửa đường thẳng OM tạo với tia OC một góc bằng 45° và tạo với hai tia OA, OB thành hai góc nhọn bằng nhau. Hãy phân tích vectơ $\overrightarrow{OM}$ theo ba vectơ $\overrightarrow{OA}$, $\overrightarrow{OB}$, $\overrightarrow{OC}$.
Bài 13. Cho hình hộp chữ nhật $ABCD.A_{1}B_{1}C_{1}D_{1}$. Đặt $\overrightarrow{B_{1}A_{1}}$ = $\vec{i}$, $\overrightarrow{B_{1}B}$ = $\vec{j}$, $\overrightarrow{B_{1}C_{1}}$ = $\vec{k}$. M, N là hai điểm theo thứ tự thuộc $AC_{1}$, $CD_{1}$ và thoả mãn:
$\overrightarrow{MA}$ = $\alpha$ $\overrightarrow{MC_{1}}$, $\overrightarrow{NC}$ = $\beta$$\overrightarrow{ND_{1}}$
a. Hãy biểu diễn các vectơ $\overrightarrow{B_{1}M}$, $\overrightarrow{B_{1}N}$ theo ba vectơ $\vec{i}$, $\vec{j}$, $\vec{k}$ và $\alpha$, $\beta$.
b. Xác định $\alpha$, $\beta$ để MN // $B_{1}D$.
c. Tính độ dài đoạn thẳng MN.
Bài 14. Cho hình hộp $ABCD.A_{1}B_{1}C_{1}D_{1}$. Chứng minh rằng hình hộp này là hình hộp chữ nhật khi và chỉ khi:
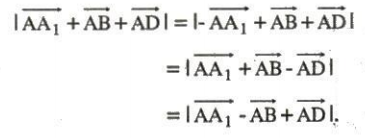
Bài toán 4: Xác định điểm M thoả một đẳng thức vectơ cho trước.
PHƯƠNG PHÁP CHUNG
1. Ta biến đổi đẳng thức vectơ cho trước về dạng
$\overrightarrow{OM}$ = $\vec{v}$, trong đó điểm O và vectơ $\vec{v}$ đã biết.
2. Nếu muốn dựng điểm M, ta lấy O làm gốc dựng một vectơ bằng vectơ $\vec{v}$, khi đó điểm ngọn của vectơ này chính là điểm M.
Ví dụ 1: Cho hình hộp $ABCD.A_{1}B_{1}C_{1}D_{1}$.
a. Chứng minh rằng $\overrightarrow{AC_{1}}$ + $\overrightarrow{A_{1}C}$ = 2$\overrightarrow{AC}$.
b. Xác định vị trí của điểm O sao cho:
.png)
c. Chứng minh rằng khi đó với mọi điểm M trong không gian ta luôn có:
.png)
Giải
a. Ta có:
.png)
b. Gọi O là giao điểm của $AC_{1}$ và $A_{1}C$, ta có ngay:
.png)
c. Ta có:
.png)
BÀI TẬP ĐỀ NGHỊ
Bài 15. Cho tứ diện ABCD. Tìm điểm G sao cho:
$\overrightarrow{GA}$ + $\overrightarrow{GB}$ + $\overrightarrow{GC}$ + $\overrightarrow{GD}$ = $\vec{0}$.
Chứng tỏ rằng điểm G đó là duy nhất và khi đó G gọi là trọng tâm của tứ diện ABCD.
Bài 16. Cho hình chóp SABCD. Tìm điểm O sao cho:
$\overrightarrow{OA}$ + $\overrightarrow{OB}$ + $\overrightarrow{OC}$ + $\overrightarrow{OD}$ + $\overrightarrow{OS}$ = $\vec{0}$.
Bài 17. Trong không gian, cho ba điểm A, B, C cố định không thẳng hàng, M là điểm di động.
a. Chứng minh rằng vectơ $\vec{v}$ = 2$\overrightarrow{MA}$ + $\overrightarrow{MB}$ - 3$\overrightarrow{MC}$ là một vectơ không phụ thuộc vào vị trí của điểm M.
b. $M_{0}$ là điểm thoả mãn $\overrightarrow{AM_{0}}$ = $\vec{v}$ và giả sử đường thẳng $AM_{0}$ cắt BC tại N. Chứng minh rằng $\overrightarrow{NB}$ = 3$\overrightarrow{NC}$.
c. Gọi (P) là mặt phẳng đi qua tâm đường tròn ngoại tiếp $\Delta$ABC và vuông góc với $\vec{v}$. Chứng tỏ rằng khi M di chuyển trong mặt phẳng (P) thì tổng sau có giá trị không đổi:
.png)
Bài 18. Cho tứ diện ABCD. Gọi E là trọng tâm $\Delta$BCD, I, $I_{1}$, J, $J_{1}$, K, $K_{1}$ theo thứ tự là trung điểm của AB, CD, CA, BD, AD, BC. Điểm G thoả mãn hệ thức:
$\overrightarrow{GA}$ + $\overrightarrow{GB}$ + $\overrightarrow{GC}$ + $\overrightarrow{GD}$ = $\vec{0}$.
Chứng minh rằng:
a. .png)
b. Ba điểm A, E, G thẳng hàng.
Bài toán 5: Tìm quỹ tích điểm M thoả mãn điều kiện K.
PHƯƠNG PHÁP CHUNG
Với các bài toán quỹ tích ta cần nhớ rằng:
1. Nếu |$\overrightarrow{MA}$| = |$\overrightarrow{MB}$|, với A, B cho trước thì M thuộc mặt phẳng trung trực của đoạn AB.
2. |$\overrightarrow{MC}$| = k|$\overrightarrow{AB}$|, với A, B, C cho trước thì M thuộc mặt cầu tâm C, bán kính bằng k.AB.
3. Nếu $\overrightarrow{MA}$ = k$\overrightarrow{BC}$, với A, B, C cho trước thì:
• Với k $\in$ R điểm M thuộc đường thẳng qua A song song với BC.
• Với k $\in$ $R^{+}$ điểm M thuộc nửa đường thẳng qua A song song với BC theo hướng $\overrightarrow{BC}$.
• Với k $\in$ $R^{-}$ điểm M thuộc nửa đường thẳng qua A song song với BC ngược hướng $\overrightarrow{BC}$.
Ví dụ 1: Trong không gian, cho ba điểm A, B, C cố định không thẳng hàng, tìm tập hợp các điểm M sao cho:
.png)
Giải
Gọi G là trọng tâm $\Delta$ABC, ta biến đổi được (1) về dạng:
.png)
⇔ M thuộc mặt cầu tâm G, bán kính GA.
Ví dụ 2: Cho tứ diện ABCD, hai điểm M, N thoả mãn:
.png)
Chứng tỏ rằng khi t thay đổi thì trung điểm I của MN di chuyển trên một đường thẳng cố định.
Giải
.png)
Gọi E, F theo thứ tự là trung điểm của AB và CD, ta có:
.png)
.png)
suy ra:
.png)
Vậy, khi t thay đổi thì trung điểm I của MN di chuyển trên đường thẳng EF
BÀI TẬP ĐỀ NGHỊ
Bài 19. Cho ba tia Ax, By, Cz song song, cùng hướng và không cùng nằm trong một mặt phẳng. Gọi M, N, P là ba điểm di động theo thứ tự trên các tia Ax, By, Cz sao cho $\overrightarrow{AM}$ = $\overrightarrow{BN}$ = $\overrightarrow{CP}$.
a. Tìm tập hợp trung điểm I của MN.
b. Tìm tập hợp trọng tâm G của $\Delta$MNP.
