Đường thẳng vuông góc với mặt phẳng

§3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

A. TÓM TẮT LÍ THUYẾT

1. ĐỊNH LÍ MỞ ĐẦU

Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b nằm trong mặt phẳng $\alpha$ thì nó vuông góc với mọi đường thẳng nằm trong $\alpha$.

Như vậy:

2. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

Định nghĩa: Một đường thẳng gọi là vuông góc với một mặt phẳng khi nó vuông góc với mọi đường thẳng chứa trong mặt phẳng đó.

Khi đường thẳng a vuông góc với mặt phẳng $\alpha$, ta kí hiệu là a $\perp$ $\alpha$ hay $\alpha$ $\perp$ a.

Định lí 1:

Từ một điểm O cho trước, ta dựng được một và chỉ một mặt phẳng vuông góc với một đường thẳng d cho trước.

Cách dựng:

• Qua O dựng đường thẳng d' // d.

• Lấy hai mặt phẳng phân biệt (P) và (Q) cùng đi qua d'. Trong (P) dựng đường thẳng a qua O và vuông góc với d'. Trong (Q) dựng đường thẳng b qua O và vuông góc với d'

Khi đó (a, b) chính là mặt phẳng cần dựng.

Hệ quả 1: Cho trước điểm O và đường thẳng a. Nếu qua O ta dựng đường thẳng b vuông góc với a thì b chứa trong mặt phẳng qua O vuông góc với a.

Hệ quả 2: Cho hai đường thẳng vuông góc với nhau. Khi đó có một và chỉ một mặt phẳng chứa đường thẳng này và vuông góc với đường thẳng kia.

Định lí 2:

Từ một điểm O cho trước ta dựng được một và và chỉ một đường thẳng d vuông góc với một mặt phẳng $\alpha$ cho trước.

Cách dựng:

• Lấy đường thẳng a nằm trong $\alpha$.

• Dựng mặt phẳng (P) qua O vuông góc với a cắt $\alpha$ theo giao tuyến b.

• Trong (P) dựng đường thẳng d qua O và vuông góc với b

Khi đó d chính là đường thẳng cần dựng.

3. LIÊN HỆ GIỮA QUAN HỆ SONG SONG VÀ QUAN HỆ VUÔNG GÓC CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG

Chúng ta có các mối liên hệ sau:

1.

Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

Tức là:

2.

Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.

Tức là:

3.

Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

Tức là:

4.

Cho hai đường thẳng phân biệt cùng vuông góc một mặt phẳng thì song song với nhau.

Tức là:

5.

Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng thì song song với nhau.

Tức là:

4. PHÉP CHIẾU VUÔNG GÓC

Định nghĩa: Phép chiếu song song trong đó phương chiếu vuông góc với mặt chiếu gọi là phép chiếu vuông góc.

Chú ý: Phép chiếu vuông góc có đầy đủ các tính chất của phép chiếu song song.

Định lí 3 (Định lí ba đường vuông góc):

Cho đường thẳng a không vuông góc với mặt phẳng $\alpha$. Một đường thẳng b nằm trong $\alpha$ vuông góc với đường thẳng a khi và chỉ khi b vuông góc với hình chiếu của a trên $\alpha$.

Tức là, với a' là hình chiếu vuông góc của a lên $\alpha$ thì:

a $\perp$ b $\subset$ $\alpha$ ⇔ a' $\perp$ b.

5. MẶT PHẲNG TRUNG TRỰC

Định nghĩa: Mặt phẳng trung trực của một đoạn thẳng là mặt phẳng vuông góc với đoạn thẳng đó tại trung điểm của nó.

Định lí 4: Tập hợp những điểm cách đều hai đầu của một đoạn thẳng là mặt phẳng trung trực của đoạn thẳng đó.

6. PHÉP ĐỐI XỨNG QUA MỘT MẶT PHẲNG

Định nghĩa: Phép đối xứng qua mặt phẳng $\alpha$ là phép cho tương ứng với mỗi điểm M trong không gian một điểm M' sao cho $\alpha$ là mặt phẳng trung trực của đoạn MM'.

B. PHƯƠNG PHÁP GIẢI TOÁN

Bài toán 1: Chứng minh đường thẳng vuông góc với mặt phẳng - Mặt phẳng trung trực. Chứng minh hai đường thẳng vuông góc với nhau.

PHƯƠNG PHÁP CHUNG

1. Để chứng minh đường thẳng a vuông góc với mặt phẳng $\alpha$, ta có thể lựa chọn một trong các cách sau:

Cách 1: Chứng minh a vuông góc với hai đường thẳng cắt nhau chứa trong $\alpha$.

Cách 2: Chứng minh a song song với đường thẳng b vuông góc với $\alpha$.

2. Để chứng minh mặt phẳng $\alpha$ là mặt phẳng trung trực của đoạn AB ta đi chứng minh $\alpha$ vuông góc với AB tại trung điểm I của AB

3. Để chứng minh hai đường thẳng a, b vuông góc với nhau, ta có thể lựa chọn một trong các cách sau:

Cách 1: Chứng minh đường thẳng a vuông góc với một mặt phẳng chứa đường thẳng b.

Cách 2: Sử dụng định lí ba đường vuông góc.

Cách 3: Nếu hai đường thẳng ấy cắt nhau thì có thể áp dụng các phương pháp đã học trong hình học phẳng.

Ví dụ 1: Gọi I là một điểm bất kì ở trong đường tròn (O), tâm O, bán kính bằng R. CD là dây cung của đường tròn (O) qua I. Trên đường thẳng vuông góc với mặt phẳng chứa đường tròn (O) tại I ta lấy điểm S với OS = R. Gọi E là điểm đối tâm của D trên đường tròn (O).

a. Chứng minh rằng $\Delta$SDE vuông tại S

b. Chứng minh rằng SD $\perp$ CE.

c. Chứng minh rằng $\Delta$SCD vuông.

Giải

a. Trong $\Delta$SDE, ta có:

SO là đường trung tuyến,

suy ra $\Delta$SDE vuông tại S.

b. Ta có ngay:

CE $\perp$ SI, vì SI vuông góc với đáy

CE $\perp$ CD, góc chắn nửa đường tròn

suy ra:

CE $\perp$ (SCD) ⇒ CE $\perp$ SD. (1)

c. Từ kết quả câu a), ta có:

SE $\perp$ SD. (2)

Từ (1) và (2) suy ra:

(SCE) $\perp$ SD ⇒ SC $\perp$ SD ⇒ $\Delta$SCD vuông tại S.

Ví dụ 2: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu vuông góc của điểm O trên mặt phẳng (ABC).

a. Chứng minh rằng BC $\perp$ (OAH), CA $\perp$ (OBH), AB $\perp$ (OCH).

b. Chứng minh rằng H là trực tâm của $\Delta$ABC.

c. Chứng minh rằng

d. Chứng minh rằng các góc của tam giác ABC đều nhọn.

Giải

a. Từ giả thiết:

OH $\perp$ (ABC) ⇒ OH $\perp$ BC. (1)

Ta có:

(2)

Từ (1) và (2) suy ra BC $\perp$ (OAH).

Chứng minh tương tự ta nhận được CA $\perp$ (OBH), AB $\perp$ (OCH).

b. Từ kết quả câu a), ta có:

BC $\perp$ (OAH) ⇒ BC $\perp$ AH. (3)

AC $\perp$ (OBH) ⇒ AC $\perp$ BH. (4)

Từ (3) và (4) suy ra H là trực tâm của $\Delta$ABC.

c. Giả sử AH cắt BC tại K, suy ra OK $\perp$ BC.

• Trong $\Delta$OBC vuông tại O, ta có:

• Trong $\Delta$OAK vuông tại O, ta có:

d. Giả sử OA = a, OB = b, OC = c.

Xét $\Delta$ABC vuông tại O, ta có:

⇒ góc $\widehat{BAC}$ nhọn.

Chứng minh tương tự, ta được các góc ABC, ACB đều nhọn.

Vậy, các góc của tam giác ABC đều nhọn.

Chú ý: Ví dụ trên đã trình bày cách chứng minh các tính chất cơ bản của tứ diện vuông.

Ví dụ 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc với mặt phẳng (ABCD). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A trên SB, SC, SD.

a. Chứng minh rằng BC $\perp$ (SAB), CD $\perp$ (SAD).

b. Chứng minh rằng (SAC) là mặt phẳng trung trực của đoạn BD.

c. Chứng minh rằng AH, AK cùng vuông góc với SC. Từ đó suy ra ba đường thẳng AH, AI, AK cùng chứa trong một mặt phẳng.

d. Chứng minh rằng (SAC) là mặt phẳng trung trực của đoạn HK. Từ đó suy ra HK $\perp$ AI.

e. Tính diện tích tứ giác AHIK, biết SA = AB = a.

Giải

a. Từ giả thiết:

SA $\perp$ (ABCD) ⇒ SA $\perp$ BC. (1)

Mặt khác, ta có:

AB $\perp$ BC, vì ABCD là hình vuông. (2)

Từ (1) và (2) suy ra BC $\perp$ (SAB).

Chứng minh tương tự ta được CD $\perp$ (SAD).

b. Từ giả thiết:

SA $\perp$ (ABCD) ⇒ SA $\perp$ BD. (3)

Mặt khác, ta có:

AC $\perp$ BD, vì ABCD là hình vuông. (4)

Từ (3) và (4) suy ra:

BD $\perp$ (SAC) tại trung điểm O của BD.

Vậy, (SAC) là một trung trực của đoạn BD.

c. Từ giả thiết và kết hợp với kết quả câu a), ta được:

Chứng minh tương tự ta được AK $\perp$ SC.

Như vậy, vì AH, AI, AK cùng vuông góc với SC nên ba đường thẳng AH, AI, AK cùng chứa trong mặt phẳng qua A và vuông góc với SC.

d. Giả sử HK cắt AI tại E.

Nhận xét rằng:

$\Delta$SAB = $\Delta$SAD (c.g.c) ⇒ SH = SK.

Trong $\Delta$SBD, ta có:

⇒ HK // BD và E là trung điểm của HK.

Kết hợp với kết quả ở câu a), suy ra:

HK $\perp$ (SAC) tại trung điểm E của HK.

Vậy, (SAC) là mặt phẳng trung trực của đoạn HK.

Từ kết quả HK $\perp$ (SAC) suy ra HK $\perp$ AI.

e. Ta có:

(5)

trong đó:

• Trong $\Delta$SAC vuông tại A, ta được:

• Trong $\Delta$SBD, ta được:

Thay (6), (7) vào (5), ta được:

Ví dụ 4: Cho hình chóp S.ABCD, đáy là hình vuông cạnh bằng a. Mặt bên SAB là tam giác đều; SCD là tam giác vuông cân đỉnh S. Gọi I, J lần lượt là trung điểm của AB và CD.

a. Tính các cạnh của $\Delta$SIJ và chứng minh rằng SI $\perp$ (SCD), SJ $\perp$ (SAB).

b. Gọi H là hình chiếu vuông góc của S trên IJ. Chứng minh rằng SH $\perp$ AC và tính độ dài SH.

c. Gọi M là một điểm thuộc đường thẳng CD sao cho BM $\perp$ SA. Tính AM theo a.

Giải

a. Xét $\Delta$SIJ, ta lần lượt có:

IJ = a, đường trung bình của hình vuông.

SI = $\large \frac{a\sqrt{3}}{2}$, đường cao trong tam giác đều

SJ = $\large \frac{1}{2}$CD = $\large \frac{a}{2}$, trung tuyến thuộc cạnh huyền của tam giác vuông.

Nhận xét rằng:

⇒ $\Delta$SIJ vuông tại S ⇔ SI $\perp$ SJ.

Khi đó, với:

Chứng minh tương tự, ta được SJ $\perp$ (SAB).

b. Ta có:

SH $\perp$ CD , theo kết quả trong a) có CD $\perp$ (SIJ)

SH $\perp$ IJ , theo giả thiết

suy ra:

SH $\perp$ (ABCD) ⇒ SH $\perp$ AC.

Trong $\Delta$SIJ ta có:

c. Điều kiện để:

BM $\perp$ SA ⇔ BM $\perp$ AH, theo định lí ba đường vuông góc.

Ta có ngay $\Delta$AIH và $\Delta$BCM là hai tam giác vuông đồng dạng, suy ra:

(1)

Trong $\Delta$SIH ta có:

(2)

Thay (2) vào (1) ta được:

Khi đó, trong $\Delta$ADM ta có:

BÀI TẬP ĐỀ NGHỊ

Bài 1. Cho hình tứ diện SABC có $\Delta$ABC vuông tại B và SA $\perp$ (ABC).

a. Chứng minh rằng BC $\perp$ (SAB).

b. Gọi AH là đường cao của $\Delta$SAB. Chứng minh rằng AH $\perp$ SC

Bài 2. Cho hình tứ diện ABCD có $\Delta$ABC và $\Delta$DBC là hai tam giác cân có chung đáy, gọi I là trung điểm của cạnh BC.

c. Chứng minh rằng BC $\perp$ AD, từ đó suy ra BC $\perp$ (AID).

d. Vẽ đường cao AH của $\Delta$AID. Chứng minh rằng AH $\perp$ (BCD).

Bài 3. Cho hình tứ diện ABCD có AB $\perp$ CD và AC $\perp$ BD. Chứng minh rằng AD $\perp$ BC.

Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, biết rằng SB = SD.

a. Chứng minh rằng (SAC) là mặt phẳng trung trực của đoạn BD.

b. Gọi H, K theo thứ tự là hình chiếu vuông góc của A trên SB và SD.

Chứng minh rằng SH = SK, OH = OK và HK // BD

c. Chứng minh rằng (SAC) là mặt phẳng trung trực của đoạn HK.

Bài 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng SA = SC và SB = SD.

a. Chứng minh rằng SO $\perp$ (ABCD) và AC $\perp$ SD.

b. Gọi I, J lần lượt là trung điểm của các cạnh BA, BC. Chứng minh rằng IJ $\perp$ (SBD).

Bài 6. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a. Mặt bên SAB là tam giác đều SC = $a\sqrt{2}$. Gọi H và K lần lượt là trung điểm của các cạnh AB và AD.

a. Chứng minh rằng SH $\perp$ (ABCD).

b. Chứng minh rằng AC $\perp$ SK và CK $\perp$ SD.

Bài 7. Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) và SA = a, đáy ABCD là hình thang vuông đường cao AB = a, BC = 2a. Ngoài ra còn có SC vuông góc với BD.

a. Chứng minh rằng $\Delta$SBC vuông.

b. Tính AD.

c. Gọi M là một điểm trên đoạn SA, đặt AM = x, với 0 $\leq$ x $\leq$ a. Tính độ dài của đường thẳng cao DE trong $\Delta$BDM theo a và x. Xác định x để DE có giá trị lớn nhất, nhỏ nhất.

Bài 8. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và SA = 2a, ABC là tam giác vuông tại C với AB = 2a, $\widehat{BAC}$ = 30°. Gọi M là một điểm di động trên cạnh AC, H là hình chiếu vuông góc của S trên BM.

a. Chứng minh rằng AH $\perp$ BM.

b. Đặt AM = x, với 0 $\leq$ x $\leq$ $\sqrt{3}$. Tính khoảng cách từ S đến BM theo a và x. Tìm các giá trị của x để khoảng cách này có giá trị nhỏ nhất, lớn nhất.

Bài 9. Cho $\Delta$ABC có BC = 2a và đường cao AD = a. Trên đường thẳng vuông góc với (ABC) tại A ta lấy điểm S sao cho SA = $a\sqrt{2}$. Gọi E, F theo thứ tự là trung điểm của SB và SC.

a. Chứng minh rằng BC $\perp$ (SAD).

b. Gọi H là hình chiếu của A trên EF. Chứng minh rằng AH nằm trong (SAD). Hãy cho biết vị trí của điểm H đối với hai điểm S và D.

c. Tính diện tích của $\Delta$AEF.

Bài 10. Cho hình lăng trụ $ABC.A_{1}B_{1}C_{1}$ có đáy ABC là tam giác đều cạnh bằng a, cạnh bên $AA_{1}$ = a và vuông góc với đáy.

a. Gọi I là trung điểm BC. Chứng minh rằng AI $\perp$ $BC_{1}$.

b. Gọi M là trung điểm $BB_{1}$. Chứng minh rằng AM $\perp$ $BC_{1}$.

c. Gọi K là điểm trên đoạn $A_{1}B_{1}$ sao cho và J là trung điểm $B_{1}C_{1}$. Chứng minh rằng AM $\perp$ (MKJ).

Bài toán 2: Thiết diện qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

PHƯƠNG PHÁP CHUNG

Để tìm thiết diện của khối đa diện (S) với mặt phẳng $\alpha$, $\alpha$ qua điểm M cho trước và vuông góc với một đường thẳng d cho trước, ta lựa chọn một trong hai cách sau:

Cách 1: Dựng mặt phẳng $\alpha$ như sau:

• Dựng hai đường thẳng cắt nhau cùng vuông góc với d, trong đó có ít nhất một đường thẳng qua M.

• Mặt phẳng xác định bởi hai đường thẳng trên chính là $\alpha$.

• Xác định thiết diện theo phương pháp đã học.

Cách 2: Nếu có hai đường thẳng cắt nhau hay chéo nhau a, b cùng vuông góc với d thì:

$\alpha$ // a hay chứa a

$\alpha$ // b hay chứa b

Ví dụ 1: Cho hình tứ diện S.ABC có ABC là tam giác đều cạnh bằng a. SA = a và vuông góc với mặt phẳng (ABC). Gọi M là một điểm tuỳ ý trên cạnh AC, $\alpha$ là mặt phẳng qua M và vuông góc với AC.

a. Tuỳ theo vị trí của điểm M trên cạnh AC, có nhận xét gì về thiết diện tạo bởi $\alpha$ với tứ diện S.ABC.

b. Đặt CM = x, với 0 < x < a. Tính diện tích S của thiết diện trên theo a và x và xác định x để diện tích này có giá trị lớn nhất. Tính diện tích lớn nhất đó.

Giải

a. Gọi E là trung điểm của AC, ta có ngay BE $\perp$ AC. Do đó, cần xét hai trường hợp khác nhau về vị trí của điểm M trên cạnh AC và trong đó ta sử dụng:

SA $\perp$ (ABC) ⇒ SA $\perp$ AC.

Trường hợp 1:

Với M thuộc đoạn CE, ta thực hiện:

• Trong (ABC) dựng Mx // BE và cắt BC tại N (ta được MN $\perp$ AC).

• Trong (SAC) dựng My // SA và cắt SC tại P (ta được MP $\perp$ AC).

Như vậy, trong trường hợp này ta được thiết diện là $\Delta$MNP vuông tại M.

Trường hợp 2:

Với M thuộc đoạn AE (trừ điểm E).

• Trong (ABC) dựng Mx // BE và cắt AC tại N (ta được MN $\perp$ AC).

• Trong (SAC) dựng My // SA và cắt SC tại P (ta được MP $\perp$ AC).

• Trong (SAB) dựng Nz // SA và cắt SB tại Q (ta được NQ $\perp$ AC).

Như vậy, trong trường hợp này ta được thiết diện là hình thang vuông MNQP (vuông tại M và N).

b. Ta xét hai trường hợp của điểm M

Trường hợp 1: Với M thuộc đoạn CE, ta có 0 < x $\leq$ $\large \frac{a}{2}$ và diện tích $\Delta$MNP là:

(1)

Trong $\Delta$BCE, ta có:

(2)

Trong $\Delta$SAC, ta có:

(3)

Thay (2), (3) vào (1), ta được:

ta có ngay:

đạt được khi x = $\large \frac{a}{2}$

Trường hợp 2: Với M thuộc đoạn AE, ta có $\large \frac{a}{2}$ < x < a và diện tích MNQP là:

(4)

Trong $\Delta$ABE, ta có:

(5)

Vì $\Delta$SAC vuông cân tại A nên $\Delta$PMC vuông cân tại N, do đó:

MP = CE = x - Cách tính thứ hai. (6)

Trong $\Delta$SAB, ta có:

(7)

Thay (5), (6), (7) vào (4), ta được:

ta biến đổi tiếp:

Tóm lại, ta được:

Ví dụ 2: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh bằng a, SA = $a\sqrt{2}$ và vuông góc với (ABCD). Gọi AH là đường cao của $\Delta$SAB.

a. Tính tỉ số $\large \frac{SH}{SB}$ và độ dài AH.

b. Gọi $\alpha$ là mặt phẳng qua A và vuông góc với SB, $\alpha$ cắt hình chóp S.ABCD theo thiết diện là hình gì ? Tính diện tích của thiết diện.

Giải

a. Trong $\Delta$SAB vuông tại S, ta có:

b. Dựng thiết diện:

• Trong (SBC) dựng Hx $\perp$ SB và cắt SC tại I.

• Nối D với I, ta được thiết diện là tứ giác AHID.

Nhận xét rằng:

Trong mặt phẳng (SBC), ta có:

⇒ AHID là hình thang vuông tại A và H.

Trong $\Delta$SBC, ta có:

Từ đó:

Ví dụ 3: Cho hình vuông ABCD cạnh bằng a. Trên đường thẳng vuông góc với mặt phẳng (ABCD) tại A lấy điểm S sao cho SA = $a\sqrt{2}$. Gọi $\alpha$ là mặt phẳng qua A và vuông góc với SC, $\alpha$ cắt SB, SC, SD lần lượt tại M, N, P.

a. Chứng minh rằng AM $\perp$ SB, AP $\perp$ SD và SM.SB = SN.SC = SP.SD = $SA^{2}$.

b. Chứng minh rằng tứ giác AMNP nội tiếp được và có hai đường chéo vuông góc với nhau.

c. Gọi O là giao điểm của AC và BD; K là giao điểm của AN và MP. Chứng minh rằng ba điểm S, K, O thẳng hàng.

d. Tính diện tích tứ giác AMNP.

Giải

Dựng thiết diện:

• Trong (SAC) dựng AN $\perp$ SC.

• Trong (SBC) dựng Nx $\perp$ SC và cắt SB tại M.

• Trong (SCD) dựng Ny $\perp$ SC và cắt SD tại P.

Thấy ngay A, M, N, P đồng phẳng vì cùng thuộc mặt phẳng qua N (hoặc A) và vuông góc với SC.

a. Ta có:

(1)

Mặt khác, theo cách dựng ta có:

SC $\perp$ (AMNP) ⇒ SC $\perp$ AM. (2)

Từ (1) và (2) suy ra:

AM $\perp$ (SBC) ⇒ AM $\perp$ SB.

Chứng minh tương tự, ta được AP $\perp$ SD.

Các $\Delta$SAB, $\Delta$SAC, $\Delta$SAD cùng vuông tại A và lần lượt có các đường cao AM, AN, AP, suy ra:

$SA^{2}$ = SM.SB = SN.SC = SP.SD. (3)

b. Ta có:

⇒ AMNP nội tiếp đường tròn đường kính AN.

Nhận xét rằng:

Dễ thấy SB = SD, do đó từ (3):

⇒ MP // BD ⇒ MP $\perp$ AN.

Vậy, tứ giác AMNP nội tiếp được và có hai đường chéo vuông góc với nhau.

c. Ta có:

d. Ta có:

(4)

trong đó:

• Trong $\Delta$SAC vuông tại A, ta được:

• Trong $\Delta$SBD, ta được:

Thay (5), (6) vào (4), ta được:

BÀI TẬP ĐỀ NGHỊ

Bài 11. Cho hình tứ diện S.ABC có ABC là tam giác đều cạnh bằng a, SA = 2a và vuông góc với mặt phẳng (ABC). Gọi $\alpha$ là mặt phẳng qua B và vuông góc với SC. Tìm thiết diện của tứ diện với $\alpha$ và tính diện tích của thiết diện này.

Bài 12. Cho hình tứ diện S.ABC có ABC là tam giác vuông cân đỉnh B, AB = a. SA = a và vuông góc với mặt phẳng (ABC). Gọi $\alpha$ là mặt phẳng qua trung điểm M của AB và vuông góc với SB.

a. Tìm thiết diện của tứ diện với $\alpha$. Thiết diện là hình gì ?

b. Tính diện tích của thiết diện.

Bài 13. Cho hình tứ diện S.ABC có ABC là tam giác vuông cân đỉnh B, AB = a. SA = $a\sqrt{2}$ và vuông góc với (ABC). Gọi $\alpha$ là mặt phẳng trung trực của SB, O là trung điểm của BC, d là đường thẳng qua O và vuông góc với (ABC).

a. Tìm giao điểm K của d với mặt phẳng $\alpha$

b. Tính độ dài OK.

Bài 14. Cho hình tứ diện S.ABC có ABC là tam giác vuông cân đỉnh B, AB = a. SA = $a\sqrt{3}$ và vuông góc với (ABC). M là một điểm tuỳ ý trên cạnh AB, đặt AM = x, với 0 < x < a. Gọi $\alpha$ là mặt phẳng qua M và vuông góc với AB. Tìm thiết diện của tứ diện với $\alpha$ và tính diện tích của nó.

Bài 15. Cho hình tứ diện S.ABC có hai mặt ABC và SBC là các tam giác đều cạnh bằng a và SA = $\large \frac{a\sqrt{3}}{2}$. M là một điểm tuỳ ý trên cạnh AB, đặt AM = x, với 0 < x < a. Gọi $\alpha$ là mặt phẳng qua M và vuông góc với BC.

a. Gọi D là trung điểm BC. Chứng minh rằng $\alpha$ // (SAD)

b. Tìm thiết diện của tứ diện SABC với $\alpha$. Thiết diện là hình gì ?

c. Tính diện tích của thiết diện theo a và x.

Bài 16. Cho tam giác đều ABC có đường cao AH = 2a. Gọi O là trung điểm AH. Trên đường thẳng vuông góc với mặt phẳng (ABC) tại O, lấy điểm S sao cho OS = 2a. Gọi I là một điểm trên OH, đặt x = AI, với a < x < 2a. Gọi $\alpha$ là mặt phẳng qua I và vuông góc với OH.

a. Tìm thiết diện của tứ diện SABC với $\alpha$. Thiết diện là hình gì ?

b. Tính diện tích của thiết diện theo a và x

Bài 17. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a, SA = 2a và vuông góc với mặt phẳng (ABCD). Gọi M là một điểm trên cạnh AB, $\alpha$ là mặt phẳng qua M, vuông góc với AB. Đặt x = AM, với 0 < x < a.

a. Tìm thiết diện của hình chóp S.ABCD với $\alpha$. Thiết diện là hình gì ?

b. Tính diện tích thiết diện theo a và x

Bài 18. Cho hình vuông ABCD cạnh bằng a, tâm O. Trên đường thẳng vuông góc với mặt phẳng (ABCD) tại O lấy điểm S sao cho SO = $\large \frac{a\sqrt{6}}{2}$. Gọi $\alpha$ là mặt phẳng qua A và vuông góc với SC, $\alpha$ cắt SB, SC, SD lần lượt tại M, N, P.

a. Tính độ dài đoạn AN. Chứng minh rằng N là trung điểm SC.

b. Chứng minh rằng MP// BD. Từ đó, suy ra cách dựng M và P.

c. Chứng minh rằng tứ giác AMNP có hai đường chéo vuông góc với nhau. Tính diện tích của tứ giác này.

Bài 19. Cho hình thoi ABCD có tâm O với các đường chéo AC = 4a, BD = 2a. Trên đường thẳng vuông góc với (ABCD) tại O ta lấy điểm S sao cho SO = 2a$\sqrt{3}$. Mặt phẳng $\alpha$ qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại M, N, P.

a. Chứng minh tứ giác AMNP có hai đường chéo vuông góc với nhau. Tính diện tích tứ giác AMNP.

b. Chứng minh rằng MNP là tam giác đều.

Bài 20. Cho hình tứ diện SABC có ABC là tam giác đều cạnh a, SA = a và vuông góc với mặt phẳng (ABC). Tìm thiết diện của tứ diện SABC với mặt phẳng $\alpha$ và tính diện tích của thiết diện trong các trường hợp sau:

a. $\alpha$ qua S và vuông góc với BC.

b. $\alpha$ qua A và vuông góc trung tuyến SI của $\Delta$SBC.

c. $\alpha$ qua trung điểm M của SC và vuông góc với AB.

Bài toán 3: Tập hợp hình chiếu của một điểm cố định trên một đường thẳng di động.

PHƯƠNG PHÁP CHUNG

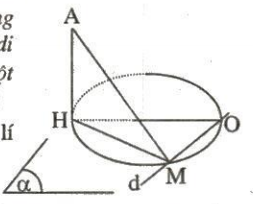
Với yêu cầu " Tìm tập hợp hình chiếu vuông góc M của điểm cố định A trên đường thẳng d di động trong mặt phẳng $\alpha$ cố định và luôn qua một điểm cố định O", ta thực hiện theo các bước sau:

Bước 1: Dựng AH $\perp$ $\alpha$ (H $\in$ $\alpha$), theo định lí ba đường vuông góc ta có:

HM $\perp$ d.

Bước 2: Trong mặt phẳng $\alpha$, vì $\widehat{HMO}$ = 90° nên M thuộc đường tròn đường kính OH chứa trong $\alpha$.

Ví dụ 1: Cho hình vuông ABCD tâm O; S là một điểm di động trên tia Ax vuông góc với mặt phẳng (ABCD).

a. Tìm tập hợp hình chiếu vuông góc của O trên đường thẳng SB.

b. Tìm tập hợp chân đường cao vẽ từ đỉnh D trong $\Delta$SDC.

Giải

a. Nhận thấy đường thẳng SB nằm trong mặt phẳng (SAB) cố định và đi qua điểm B cố định.

Hạ OH $\perp$ AB, từ giải thiết:

SA $\perp$ (ABCD) ⇒ SA $\perp$ OH ⇒ OH $\perp$ (SAB).

Gọi M là hình chiếu vuông góc của O trên đường thẳng SB, suy ra:

SB $\perp$ MH, theo định lí ba đường vuông góc

⇒ $\widehat{BMH}$ = 90° ⇒ M thuộc đường tròn đường kính BH chứa trong (SAB).

Khi S di động trên tia Ax thì M thuộc nửa đường tròn đường kính BH trong nửa mặt phẳng (SAB) bờ AB.

b. Nhận thấy đường thẳng SC nằm trong mặt phẳng (SAC) cố định và đi qua điểm C cố định.

Ta có:

Gọi N là hình chiếu vuông góc của D trên đường thẳng SC, suy ra:

ON $\perp$ SC, theo định lí ba đường vuông góc

⇒ $\widehat{ONC}$ = 90° ⇒ N thuộc đường tròn đường kính OC chứa trong (SAC).

Khi S di động trên tia Ax thì N thuộc nửa đường tròn đường kính OC trong nửa mặt phẳng (SAC) bờ AC.

Ví dụ 2: Trong mặt phẳng $\alpha$ cho góc vuông xOy, d là đường thẳng cố định trong $\alpha$, d cắt Ox, Oy lần lượt tại A và B. Gọi Oz là tia vuông góc với $\alpha$, S là một điểm trên Oz. Gọi AE, BF là đường cao của $\Delta$SAB.

a. Cho góc xOy cố định, S di động trên tia Oz. Tìm tập hợp các điểm E và F.

b. Cho S cố định, góc xOy quay quanh O. Chứng minh rằng trực tâm của $\Delta$SAB cố định. Tìm tập hợp các điểm E và F.

Giải

a. Ta lần lượt tìm tập hợp các điểm E và F.

• Tìm tập hợp điểm E: Nhận thấy đường thẳng SB nằm trong mặt phẳng (yOz) cố định và đi qua điểm B cố định.

Ta có:

⇒ OE $\perp$ SB, theo định lí ba đường vuông góc ⇒ $\widehat{OEB}$ = 90°

⇒ E thuộc đường tròn đường kính OB chứa trong (yOz).

Khi S di động trên tia Oz thì E thuộc nửa đường tròn đường kính OB trong nửa mặt phẳng (yOz) bờ Oy.

• Tìm tập hợp điểm F: Thực hiện tương tự ta được F thuộc nửa đường tròn đường kính OA trong nửa mặt phẳng (xOz) bờ Ox.

b. Giả sử AE $\cap$ BF = {H}, suy ra H là trực tâm của $\Delta$SAB và ta đi chứng minh H cố định.

Kéo dài SH cắt AB tại K, ta có:

Trong mặt phẳng (S, d) cố định và có SH cố định và:

• Vì $\widehat{SEH}$ = 90° nên E thuộc nửa đường tròn đường kính SH trong nửa mặt phẳng (SBK) bờ SK.

• Vì $\widehat{SFH}$ = 90° nên F thuộc nửa đường tròn đường kính SH trong nửa mặt phẳng (SAK) bờ SK.

BÀI TẬP ĐỀ NGHỊ

Bài 21. Cho hình chóp S.ABCD có ABCD là hình vuông tâm O, SA vuông góc với mặt phẳng (ABCD). Gọi I là trung điểm của cạnh SC, M là một điểm di động trên cạnh AD.

a. Tìm tập hợp các điểm K, hình chiếu vuông góc của I trên CM.

b. Tìm tập hợp chân đường cao E vẽ từ đỉnh B trong $\Delta$SBM.

Bài 22. Cho $\Delta$ABC đều, S là một điểm di động trên tia Ax vuông góc với mặt phẳng (ABC).

a. Tìm tập hợp hình chiếu vuông góc của A trên SB.

b. Gọi N là hình chiếu vuông góc của A trên mặt phẳng (SBC). Chứng minh rằng đường thẳng SN qua trung điểm của BC. Tìm tập hợp các điểm N.

c. Gọi K là trung điểm của cạnh SC. Chứng minh rằng BK ở trong một mặt phẳng cố định. Tìm tập hợp các hình chiếu vuông góc của A trên BK.

Bài 23. Cho $\Delta$ABC đều ở trong mặt phẳng $\alpha$. Vẽ Bx và Cy là hai tia cùng chiều và cùng vuông góc với $\alpha$. Cho M, N là hai điểm lần lượt di động trên Bx, Cy. Tìm tập hợp chân H của đường cao AH của $\Delta$AMN khi M, N di động thỏa một trong các điều kiện dưới đây:

a. BM = CN.

b. 2BM = CN.

c. BM + CN = 2a, với a là độ dài không đổi.

Bài toán 4: Tìm tập hợp hình chiếu vuông góc của một điểm cố định trên một mặt phẳng di động.

PHƯƠNG PHÁP CHUNG

Với yêu cầu " Tìm tập hợp hình chiếu vuông góc H của một điểm cố định A trên mặt phẳng $\alpha$ di động luôn chứa một đường thẳng d cố định", ta thực hiện theo các bước sau:

Bước 1: Xác định mặt phẳng $\beta$ qua A vuông góc với d. Tìm a = $\alpha \cap \beta$

Bước 2: Gọi H là hình chiếu vuông góc của A lên a, thì H cũng là hình chiếu vuông góc của A trên $\alpha$.

Bước 3: Gọi E là giao điểm của d với $\beta$. Trong mặt phẳng $\beta$, $\widehat{AHE}$ = 90° nên H thuộc đường tròn đường kính AE.

Ví dụ 1: Trong mặt phẳng $\alpha$ cho đường tròn (C), đường kính AB, SA vuông góc với $\alpha$. Gọi M là một điểm di động trên (C), H là hình chiếu vuông góc của điểm A trên mặt phẳng (SBM). Tìm tập hợp các điểm H.

Giải

Nhận thấy mặt phẳng (SBM) chứa đường thẳng SB cố định. Ta đi dựng mặt phẳng qua A và vuông góc với SB bằng cách:

• Trong (SAB) hạ AK $\perp$ SB.

• Trong (SBM) dựng Kx $\perp$ SB và cắt SM tại H.

Khi đó:

(AKH) $\perp$ SB và (AKH) $\cap$ (SBM) = KH.

Ta đi chứng minh AH $\perp$ (SBM), thật vậy:

Trong (AKH), ta có:

AH $\perp$ HK ⇔ $\widehat{AHK}$ = 90°

nên H thuộc đường tròn đường kính AK trong mặt phẳng (AKH).

Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, $\widehat{ABC}$ = 60°, SA = a và vuông góc với mặt phẳng (ABCD). Gọi M là một điểm trên cạnh SB.

a. Khi M là trung điểm của cạnh SB, tính diện tích của thiết diện của hình chóp S.ABCD với mặt phẳng (ADM).

b. Khi M di động trên cạnh SB. Tìm tập hợp hình chiếu vuông góc của S trên mặt phẳng (ADM).

Giải

a. Ta có:

⇒ Mx // AD // BC và Mx cắt SC tại N.

Khi đó, ta nhận được thiết diện AMND là hình thang.

Trong hình thang AMND hạ AK $\perp$ MN, ta được:

(1)

trong đó:

• Trong $\Delta$SBC có MN là đường trung bình nên:

(2)

• Trong $\Delta$SAB vuông tại A có AM là trung tuyến thuộc cạnh huyền nên:

(3)

• Trong $\Delta$SAC vuông tại A có AN là trung tuyến thuộc cạnh huyền nên:

(4)

• Trong $\Delta$AMN cân tại A, ta có:

(5)

Thay (2), (5) vào (1), ta được:

b.

Nhận thấy mặt phẳng (ADM) chứa đường thẳng AD cố định. Ta đi dựng mặt phẳng qua S và vuông góc với AD bằng nhận xét:

AK $\perp$ MN ⇔ AK $\perp$ AD

Khi đó:

(SAK) $\perp$ AD và (SAK) $\cap$ (ADM) = AK.

Trong (SAK) hạ SH $\perp$ AK thì H cũng là hình chiếu vuông góc của S trên (ADM).

Trong (SAK), ta có:

SH $\perp$ AH ⇔ $\widehat{SHA}$ = 90°

nên H thuộc đường tròn đường kính SA trong mặt phẳng (SAK).

Hạn chế quĩ tích – Đề nghị bạn đọc tự làm.

BÀI TẬP ĐỀ NGHỊ

Bài 24. Cho hình tứ diện S.ABC có SI vuông góc với mặt phẳng (ABC) và I là trung điểm của cạnh AB. M là một điểm di dộng trên cạnh SC. Tìm tập hợp hình chiếu vuông góc của S trên mặt phẳng (ABM).

Bài 25. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B. Gọi M là một điểm trên cạnh SA. Tìm tập hợp hình chiếu vuông góc của S trên mặt phẳng (MBC) khi M di động từ S đến A.

Bài 26. Trong mặt phẳng $\alpha$ cho đường tròn ($\gamma$) tâm O, A là điểm cố định trên ($\gamma$) và BC là dây cung di động của ($\gamma$) luôn vuông góc với OA. Trên đường thẳng vuông góc với $\alpha$ tại A lấy điểm cố định S khác A. Tìm tập hợp hình chiếu vuông góc của A trên mặt phẳng (SBC).

Bài 27. Cho hình vuông ABCD tâm O, trên tia Ax vuông góc với mặt phẳng (ABCD) lấy điểm S.

a. Cho S di động trên tia Ax. Tìm tập hợp hình chiếu vuông góc của O trên mặt phẳng (SBC).

b. Cho S cố định, M là một điểm di động trên đoạn AC. Tìm tập hợp hình chiếu vuông góc của A trên mặt phẳng (SMB).