§4 PHÉP ĐỐI XỨNG TÂM
A. TÓM TẮT LÍ THUYẾT
1. PHÉP ĐỐI XỨNG TÂM
Định nghĩa: Phép đối xứng qua điểm O là một phép dời hình biến mỗi điểm M thành M' đối xứng với M qua O, tức là $\overrightarrow{OM}$ + $\overrightarrow{OM'}$ = $\overrightarrow{0}$.
Kí hiệu Đ$_{O}$ hay $S_{O}$.
BIỂU THỨC TOẠ ĐỘ CỦA PHÉP ĐỐI XỨNG TÂM
Trong mặt phẳng với hệ trục toạ độ Oxy, cho điểm I(a; b). Phép đối xứng tâm Đ$_{I}$ biến điểm M(x; y) thành điểm M'(x';y') với:
.png)
3. TÂM ĐỐI XỨNG CỦA MỘT HÌNH
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm Đ$_{O}$ biến hình H thành chính nó, tức là Đ$_{O}$(H) = H.
B. PHƯƠNG PHÁP GIẢI TOÁN
Bài toán 1: Tìm phép đối xứng tâm biến hình ($H_{1}$) thành hình ($H_{2}$).
PHƯƠNG PHÁP CHUNG
Sử dụng định nghĩa và tính chất của phép đối xứng tâm.
Ví dụ 1: Cho hai đường tròn ($C_{1}$) và ($C_{2}$) lần lượt có tâm $O_{1}$, $O_{2}$ và đều có bán kính R. Tìm phép đối xứng tâm biến ($C_{1}$) thành ($C_{2}$).
Giải
.png)
Gọi O là trung điểm của $O_{1}O_{2}$
Lấy $M_{1}$ tuỳ ý thuộc ($C_{1}$) và gọi $M_{2}$ là ảnh của M qua Đ$_{O}$, ta có:
.png)
Ngược lại: lấy $M_{2}$ là một điểm tuỳ ý thuộc ($C_{2}$) và gọi $M_{1}$ là tạo ảnh của nó qua Đ$_{O}$ - chứng minh tương tự ta được $M_{1}$ $\in$ ($C_{1}$).
Vậy ($C_{2}$) là ảnh của ($C_{1}$) qua Đ$_{O}$
Bài toán 2: Chứng minh tính chất hình học.
PHƯƠNG PHÁP CHUNG
1. Với bài toán định tính, ta thường gặp các dạng yêu cầu sau:
Dạng 1: Chứng minh ($H_{1}$) là ảnh của ($H_{2}$) qua phép đối xứng tâm O, ta thực hiện theo các bước:
Bước 1: Lấy điểm $M_{1}$ tuỳ ý thuộc ($H_{1}$), ta đi chứng minh $M_{2}$ = $S_{O}$($M_{1}$) $\in$ ($H_{2}$).
Bước 2: Ngược lại, lấy điểm $M_{2}$ tuỳ ý thuộc ($H_{2}$), ta đi chứng minh $M_{1}$ = $S_{O}$($M_{2}$) $\in$ ($H_{1}$).
Dạng 2: Chứng minh tính chất K, ta thực hiện theo các bước:
Bước 1: Xác định một hoặc nhiều phép đối xứng tâm để thiết lập mối liên kết giữa các yếu tố.
Bước 2: Sử dụng các tính chất của phép quay để giải các yêu cầu của bài toán.
2. Với bài toán định lượng, bằng việc thiết lập được các phép đối xứng tâm thích hợp, ta có thể tính toán được các yếu tố trong một hình.
Ví dụ 1: Cho $\Delta$ABC có AM và CN là các trung tuyến. Chứng minh rằng nếu $\widehat{BAM}$ = $\widehat{BCN}$ = 30° thì $\Delta$ABC đều.
Giải
.png)
Tứ giác ACMN có $\widehat{NAM}$ = $\widehat{MCN}$ = 30° nên nội tiếp trong một đường tròn tâm O bán kính R và $\widehat{MON}$ = 2 $\widehat{NAM}$ = 60°.
Xét các phép đối xứng tâm N và tâm M.
.png)
Trong $\Delta OO_{1}O_{2}$, ta có nhận xét:
$OO_{1}$ = $OO_{2}$ = 2R,
$\widehat{MON}$ = 2 $\widehat{BAM}$ = 60°,
suy ra $\Delta OO_{1}O_{2}$ là tam giác đều.
Mặt khác:
$O_{1}B$ + $O_{2}B$ = R + R = 2R = $O_{1}O_{2}$ nên B là trung điểm của $O_{1}O_{2}$
Từ đó suy ra hai $\Delta$ABC và $\Delta OO_{1}O_{2}$ đồng dạng (vì cùng đồng dạng với $\Delta$BMN) và vì $\Delta OO_{1}O_{2}$ đều nên $\Delta$ABC đều.
Ví dụ 1: Cho hai điểm B và C cố định trên đường tròn (O; R) và một điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng tâm để chứng minh rằng trực tâm H của $\Delta$ABC nằm trên một đường tròn cố định.
Giải
.png)
Gọi I là trung điểm BC và vẽ đường kính AM.
Ta có:
BH $\perp$ AC và MC $\perp$ AC ⇒ BH // MC. (1)
CH $\perp$ AB và MB $\perp$ AB ⇒ CH // MB. (2)
Từ (1) và (2) suy ra:
BHCM là hình bình hành ⇒ I là trung điểm HM.
Vậy, trực tâm H của $\Delta$ABC nằm trên một đường tròn cố định (O'; R) = Đ$_{I}$((O; R)).
Bài toán 3: Tìm tập hợp điểm M.
PHƯƠNG PHÁP CHUNG
Ta thực hiện theo các bước:
Bước 1: Tìm một phép đối xứng tâm $S_{O}$, biến điểm E di động thành điểm M.
Bước 2: Tìm tập hợp (H) của các điểm E.
Bước 3: Kết luận tập hợp các điểm M là ảnh của (H) trong phép đối xứng tâm $S_{O}$.
Ví dụ 2: Cho đường tròn (O; R) và hai điểm A, B cố định. Với mỗi điểm M, ta xác định điểm M' sao cho $\overrightarrow{MM'}$ = $\overrightarrow{MA}$ + $\overrightarrow{MB}$. Tìm quỹ tích điểm M' khi điểm M chạy trên (O; R).
Giải
Bạn đọc tự vẽ hình
Gọi I là trung điểm của AB thì I cố định và
$\overrightarrow{MA}$ + $\overrightarrow{MB}$ = 2$\overrightarrow{MI}$
Do đó, $\overrightarrow{MM'}$ = $\overrightarrow{MA}$ + $\overrightarrow{MB}$ khi và chỉ khi $\overrightarrow{MM'}$ = 2$\overrightarrow{MI}$, tức là MM' nhận I làm trung điểm hay phép đối xứng tâm Đ$_{I}$ biến điểm M thành M'.
Vậy khi M chạy trên đường tròn (O; R) thì quỹ tích M' là ảnh của đường tròn đó qua Đ$_{I}$.
Nếu ta gọi O' là điểm đối xứng của O qua điểm I thì quỹ tích của M' là đường tròn (O; R).
Ví dụ 3: Cho đường tròn (O) và dây cung AB cố định, M là một điểm di động trên (O), M không trùng A, B. Hai đường tròn ($O_{1}$), ($O_{2}$) qua M, theo thứ tự tiếp xúc với AB tại A và B. Gọi N là giao điểm thứ hai của ($O_{1}$), ($O_{2}$)
a. Chứng minh rằng đường thẳng MN luôn qua một điểm cố định.
b. Tìm tập hợp N khi M di động trên (O).
Giải
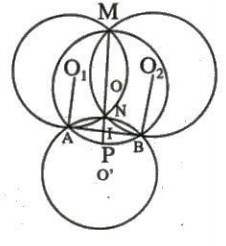
a. Gọi I là giao điểm của MN và AB, ta có:
.png)
⇒ IA = IB, do đó I là trung điểm AB.
Vậy đường thẳng MN luôn qua một điểm cố định I là trung điểm AB.
b. Gọi P là điểm chung thứ hai của MN và (O), ta có:
.png)
Từ (1) và (2) suy ra:
.png)
Vì tập hợp các điểm P là đường tròn (O) qua hai điểm A và B nên tập hợp các điểm N là đường tròn (O') bỏ đi hai điểm A và B với (O') = $S_{(I)}$(O)
Bài toán 4: Dựng hình.
PHƯƠNG PHÁP CHUNG
Ta thường thực hiện theo 4 bước đã biết.
Ví dụ 1: Cho hai đường tròn (O; R) và ($O_{1}$; $R_{1}$) cắt nhau tại hai điểm A, B. Hãy dựng một đường thẳng d đi qua A cắt (O; R) và ($O_{1}$; $R_{1}$) lần lượt tại M và $M_{1}$ sao cho A là trung điểm của $MM_{1}$.
Giải
Bạn đọc tự vẽ hình
Giả sử ta đã dựng được đường thẳng d thoả mãn yêu cầu bài toán. Gọi Đ$_{A}$ là phép đối xứng qua A thì Đ$_{A}$ biến điểm M thành điểm $M_{1}$ và biến đường tròn (O; R) thành đường tròn (O'; R).
Vì M nằm trên (O; R) nên $M_{1}$ nằm trên (O'; R).
Mặt khác, $M_{1}$ lại nằm trên ($O_{1}$; $R_{1}$) nên $M_{1}$ là giao điểm khác A của hai đường tròn (O'; R) và ($O_{1}$; $R_{1}$).
Từ đó, suy ra cách dựng:
• Dựng đường tròn (O'; R) đối xứng với (O; R) qua A (O' là điểm đối xứng với O qua A).
• Lấy giao điểm $M_{1}$ của hai đường tròn (O'; R) và ($O_{1}$; $R_{1}$), $M_{1}$ khác A.
• Đường thẳng d là đường thẳng đi qua A và $M_{1}$.
Ví dụ 2: Cho hai đường thẳng ($d_{1}$) và ($d_{2}$), hai điểm A, G không thuộc ($d_{1}$), ($d_{2}$). Hãy dựng $\Delta$ABC có trọng tâm G và hai đỉnh B và C lần lượt thuộc ($d_{1}$) và ($d_{2}$).
Giải
.png)
Phân tích: Giả sử đã dựng được $\Delta$ABC có trọng tâm G, hai đỉnh B và C lần lượt thuộc ($d_{1}$), ($d_{2}$). Gọi M là trung điểm cạnh BC thì M được xác định bởi:
.png)
Thực hiện phép đối xứng tâm M:
.png)
Ta có B $\in$ ($d'_{2}$).
Vậy B là giao điểm của ($d'_{2}$) và ($d_{1}$).
Cách dựng: Ta lần lượt thực hiện:
- Dựng .png)
- Dựng đường thẳng ($d'_{2}$) với ($d'_{2}$) = $S_{(M)}$[($d_{2}$)] và giả sử ($d'_{2}$) cắt ($d_{1}$) tại B
- Dựng điểm C với C = $S_{(M)}$(B)
thì $\Delta$ABC là tam giác cần dựng.
Chứng minh: Dựa vào cách dựng ta có:
- B $\in$ ($d_{1}$);
- B $\in$ ($d'_{2}$);
- $S_{(M)}$[($d'_{2}$)] = ($d'_{2}$) và C = $S_{(M)}$(B) ⇒ C $\in$ ($d_{2}$)
- M là trung điểm cạnh BC và .png)
⇒ G là trọng tâm $\Delta$ABC.
Biện luận: Số nghiệm hình của bài toán bằng số điểm chung của ($d_{1}$) và ($d'_{2}$)
Bài toán 5: Hệ toạ độ đối với phép đối xứng tâm.
PHƯƠNG PHÁP CHUNG
Sử dụng kết quả: Trong mặt phẳng với hệ trục toạ độ Oxy, cho điểm I(a; b).
Phép đối xứng tâm Đ$_{I}$ biến điểm M(x; y) thành điểm M'(x'; y') với:
.png)
Trong phần này chúng ta xem xét ba bài toán cơ bản và mong muốn thông qua đó các em có thể xây dựng được phương pháp giải bài toán tổng quát.
Dạng 1: Xác định điểm $M_{1}$ đối xứng với điểm M qua điểm I(a, b).
Ta có ngay I là trung điểm $MM_{1}$, do đó:
.png)
Đặc biệt: Nếu I $\equiv$ O(0; 0) thì với M(x, y) suy ra $M_{1}$($x_{1}$; $y_{1}$).
Dạng 2: Xác định phương trình đường thẳng ($d_{1}$) đối xứng với đường thẳng (d): Ax + By + C = 0 qua I(a, b).
Ta có thể lựa chọn một trong hai cách sau:
Cách 1: Thực hiện theo các bước:
Bước 1: Với mỗi điểm M(x, y) $\in$ (d), suy ra tồn tại điểm $M_{1}$($x_{1}$; $y_{1}$) $\in$ ($d_{1}$) nhận I làm trung điểm, ta được:
.png)
Bước 2: Thay (I) vào phương trình của (d), ta được:
A$x_{1}$ + B$y_{1}$ - C - 2aA - 2bB = 0. (1)
Bước 3: Viết lại (1) dưới dạng:
Ax + By - C - 2aA - 2bB = 0. (2)
Đó chính là phương trình đường thẳng ($d_{1}$).
Cách 2: Thực hiện theo các bước:
Bước 1: Lấy một điểm A $\in$ (d), từ đó xác định toạ độ điểm $A_{1}$ đối xứng với A qua I.
Bước 2: Vì ($d_{1}$) // (d): Ax + By + C = 0 suy ra
(d): Ax + By + D = 0.
Bước 3: Vì $A_{1}$ $\in$ ($d_{1}$) ⇒ giá trị của D,
Từ đó có được phương trình của ($d_{1}$).
Dạng 3: Xác định phương trình đường tròn ($C_{1}$) đối xứng với đường tròn (C): f(x, y) = 0 qua điểm E($x_{0}$; $y_{0}$) (E $\neq$ I là tâm của (C)).
.png)
Ta lựa chọn một trong hai cách sau:
Cách 1: Chúng ta thực hiện theo các bước:
Bước 1: Với mỗi M(x, y) $\in$ ($C_{1}$) thì $\exists$ $M_{1}$($x_{1}$, $y_{1}$) $\in$ (C) sao cho M đối xứng với $M_{1}$ qua E($x_{0}$; $y_{0}$)
⇔ $\exists$ $x_{1}$, $y_{1}$ thoả mãn:
.png)
Bước 2: Khử $x_{1}$, $y_{1}$ từ hệ (I) ta được phương trình của đường tròn ($C_{1}$).
Cách 2: Chúng ta thực hiện theo các bước sau:
Bước 1: Gọi I, $I_{1}$ theo thứ tự là tâm đường tròn (C), ($C_{1}$) và R là bán kính đường tròn (C). Khi đó E là trung điểm $II_{1}$ ⇒ toạ độ điểm $I_{1}$.
Bước 2: Lập phương trình đường tròn ($C_{1}$) thoả mãn:
.png)
Ví dụ 1: Trong mặt phẳng toạ độ Oxy, cho đường thẳng $\Delta$: ax + by + c = 0 và điểm I($x_{0}$; $y_{0}$). Phép đối xứng tâm Đ$_{I}$ biến đường thẳng $\Delta$ thành đường thẳng $\Delta$'. Viết phương trình của $\Delta$'.
Giải
Với mỗi điểm M($x_{0}$; $y_{0}$) $\in$ ($\Delta$) (tức là A$x_{0}$ + B$y_{0}$ + C = 0), suy ra tồn tại điểm M'(x; y) $\in$ ($\Delta$') sao cho:
.png)
Do đó, đường thẳng ($\Delta$') sẽ có phương trình:
($\Delta$'): A(2a - x) + B(2b - y) + C = 0
⇔ ($\Delta$'): Ax + By - C - 2aA - 2bB = 0.
Ví dụ 2: Cho hình bình hành ABCD biết phương trình cạnh (AB): 2x - y = 0, (AD): 4x - 3y = 0 và tâm I(2; 2). Lập phương trình các cạnh BC và CD.
Giải
• Cạnh BC đối xứng với AD qua I, ta lần lượt thực hiện:
Với mỗi điểm M(x, y) $\in$ (AD) ⇒ tồn tại điểm $M_{1}$($x_{1}$, $y_{1}$) $\in$ ($d_{1}$) nhận I làm trung điểm, ta được:
.png)
Thay (I) vào phương trình của (AD), ta được:
4(4 - $x_{1}$) - 3(4 - $y_{1}$) = 0 ⇔ 4$x_{1}$ - 3$y_{1}$ - 4 = 0. (1)
Viết lại (1) dưới dạng:
4x - 3y - 4 = 0. (2)
Đó chính là phương trình đường thẳng (BC).
• Cạnh CD đối xứng với AB qua I, ta lần lượt thực hiện:
Lấy điểm O(0; 0) $\in$ (AB), gọi $O_{1}$ là điểm đối xứng với O qua I, suy ra $O_{1}$(4; 4).
- Vì (CD) // (AB): 2x - y = 0 ⇒ (CD): 2x - y + C = 0.
- Vì $O_{1}$ $\in$ (CD) ⇒ C = - 4
Vậy phương trình đường thẳng ($d_{1}$): 2x - y - 4 = 0.
Ví dụ 3: Cho đường tròn (C): $x^{2}$ + $y^{2}$ - 4x - 2y + 3 = 0. Xác định phương trình đường tròn ($C_{1}$) đối xứng với đường tròn (C) qua điểm E(1; 2).
Giải
Cách 1: Với mỗi M(x; y) $\in$ ($C_{1}$)
⇔ $\exists$ $M_{1}$($x_{1}$; $y_{1}$) $\in$ (C) sao cho M đối xứng với $M_{1}$ qua E
⇔ $\exists$ $x_{1}$, $y_{1}$ thoả mãn:
.png)
Vậy phương trình đường tròn ($C_{1}$):
.png)
Cách 2: Xét đường tròn (C) có tâm I(2; 1) và bán kính R = $\sqrt{2}$.
Gọi $I_{1}$ là tâm đường tròn ($C_{1}$).
Vì (C) và ($C_{1}$) đối xứng qua điểm E ⇒ E là trung điểm $II_{1}$, do đó $I_{1}$(0; 3).
Phương trình đường tròn ($C_{1}$) được cho bởi:
.png)
Chú ý: Cho hàm số:
y = f(x).
1. Để chứng minh đồ thị hàm số nhận điểm I(a; b) làm tâm đối xứng, ta thực hiện theo các bước sau:
Bước 1: Với phép biến đổi toạ độ
.png)
hàm số có dạng:
Y+ b = f(X + a) ⇔ Y = F(X) (1)
Bước 2: Nhận xét rằng hàm số (1) là hàm số lẻ.
Bước 3: Vậy, đồ thị hàm số nhận điểm I(a; b) làm tâm đối xứng.
2. Để tìm điều kiện của tham số để đồ thị hàm số nhận điểm I(a, b) làm tâm đối xứng, ta thực hiện theo các bước sau:
Bước 1: Thực hiện phép biến đổi toạ độ
.png)
hàm số có dạng:
Y+ b = f(X + a) ⇔ Y = F(X) (1)
Bước 2: Đồ thị hàm số nhận I(a, b) làm tâm đối xứng
⇔ hàm số (1) là hàm số lẻ ⇒ Giá trị của tham số
Bước 3: Kết luận.
Ví dụ 4: Cho hàm số:
y = $x^{3}$ – 3$x^{2}$ + 1.
Chứng minh rằng đồ thị hàm số nhận điểm I(1;-1) làm tâm đối xứng.
Giải
Với phép biến đổi toạ độ
.png)
khi đó hàm số có dạng :
.png)
Hàm số (1) là hàm số lẻ.
Vậy, đồ thị hàm số nhận điểm I(1; -1) làm tâm đối xứng.
Chú ý : Đồ thị hàm số bậc ba
.png)
luôn nhận điểm .png) làm tâm đối xứng.
làm tâm đối xứng.
Ví dụ 5:
Cho hàm số:
.png)
Chứng minh rằng đồ thị hàm số nhận điểm I(1; 1) làm tâm đối xứng.
Giải
Với phép biến đổi toạ độ
.png)
khi đó hàm số có dạng:
.png)
Hàm số (1) là hàm số lẻ.
Vậy, đồ thị hàm số nhận điểm I(1, 1) làm tâm đối xứng.
Chú ý : Đồ thị hàm số :
.png)
luôn nhận điểm .png) làm tâm đối xứng.
làm tâm đối xứng.
Ví dụ 6:
Cho hàm số:
.png)
Chứng minh rằng đồ thị hàm số nhận điểm I(2; 2) làm tâm đối xứng.
Giải
Với phép biến đổi toạ độ
.png)
khi đó hàm số có dạng:
.png)
Hàm số (1) là hàm số lẻ
Vậy, đồ thị hàm số nhận điểm I(2; 2) làm tâm đối xứng.
Chú ý : Đồ thị hàm số .png) luôn nhận điểm
luôn nhận điểm .png) làm tâm đối xứng.
làm tâm đối xứng.
Ví dụ 7: Xác định m để đồ thị hàm số (C) nhận điểm I(1; 0) làm tâm đối xứng, biết:
.png)
Giải
Với phép biến đổi toạ độ
.png)
hàm số có dạng:
.png)
Hàm số (1) là hàm số lẻ
.png)
Vậy, với m = 1 đồ thị hàm số nhận điểm I(1; 0) là tâm đối xứng.
Ví dụ 8: Cho hàm số:
.png)
Tìm m để đồ thị hàm số nhận điểm I(2; 1) làm tâm đối xứng.
Giải
Điểm I(2, 1) là tâm đối xứng của đồ thị khi với phép biến đổi toạ độ:
.png)
hàm số sau là hàm lẻ
.png)
Xét hàm số :
.png)
Hàm số (1) là hàm lẻ khi và chỉ khi m + 4 = 0 ⇔ m = -4.
Vậy, với m = -4 đồ thị hàm số nhận I(2, 1) làm tâm đối xứng.
BÀI TẬP ĐỀ NGHỊ
Bài 1. Chỉ ra các tâm đối xứng của các hình sau đây:
a. Hình gồm hai đường thẳng cắt nhau.
b. Hình gồm hai đường thẳng song song.
c. Hình gồm hai đường tròn bằng nhau.
d. Đường elip.
e. Đường Hypebol.
Bài 2. Cho đường tròn (O; R), đường thẳng $\Delta$ và điểm I. Tìm điểm A trên (O; R) và điểm B trên $\Delta$ sao cho I là trung điểm của đoạn thẳng AB.
Bài 3. Cho đường tròn (O) với ba dây AB, MN, PQ cắt nhau tại I sao cho IA = IB và M, P nằm cùng phía với AB. Gọi E, F lần lượt là giao điểm của AB với PN. Chứng minh rằng IE = IF.
Bài 4. Cho $\Delta$ABC có H là trực tâm; M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Gọi $H_{1}$, $H_{2}$, $H_{3}$ là điểm đối xứng của H qua M, N, P theo thứ tự đó. Chứng minh rằng $H_{1}$, $H_{2}$, $H_{3}$ thuộc đường tròn ngoại tiếp tam giác $\Delta$ABC.
Bài 5. Cho $\Delta$ABC có đường tròn (O) cắt các cạnh BC, CA, AB theo thứ tự tại $A_{1}$ và $A_{2}$; $B_{1}$ và $B_{2}$; $C_{1}$ và $C_{2}$. Chứng minh rằng: nếu đường thẳng vuông góc với các cạnh của tam giác tại $A_{1}$, $B_{1}$, $C_{1}$ đồng quy thì các đường thẳng vuông góc với các cạnh của tam giác tại $A_{2}$, $B_{2}$, $C_{2}$ đồng quy.
Bài 6. Cho tam giác ABC. Vẽ các tia Ax, Ay trong góc A sao cho $\widehat{BAx}$ = $\widehat{CAy}$, vẽ các tia Bz, Bt trong góc B sao cho $\widehat{ABz}$ = $\widehat{CBt}$ . Gọi E là giao điểm của Ax và Bz, F là giao điểm Ay và Bt. Chứng minh rằng $\widehat{ACE}$ = $\widehat{BCF}$
Bài 7. Từ một điểm A ở ngoài đường tròn (O) dựng hai tiếp tuyến AB, AC của (O) (B, C là tiếp điểm). Tại một điểm M tuỳ ý của (O) dựng tiếp tuyến thứ ba, cắt AB và AC lần lượt tại D, E. Tìm tập hợp tâm đường tròn ngoại tiếp $\Delta$DOE khi M di động trên (O).
Bài 8. Cho $\Delta$ABC. Ba trung tuyến $AA_{1}$, $BB_{1}$, $CC_{1}$ cắt nhau tại G.
a. Dựng ảnh $A_{2}B_{2}C_{2}$ của $\Delta$ABC qua Đ$_{G}$.
b. Chứng minh hai tam giác $\Delta$ABC và $\Delta$$A_{2}B_{2}C_{2}$ đồng dạng. Xác định tỉ số đồng dạng.
Bài 9. Cho hình bình hành ABCD với giao điểm O của hai đường chéo. Xác định ảnh của hình bình hành này qua phép đối xứng tâm O.
Bài 10. Cho đường tròn (O), đường thẳng (d) và điểm A không phụ thuộc đường thẳng (d) và đường tròn (O). Dựng điểm B thuộc đường tròn (O) và điểm C thuộc (d) sao cho A là trung điểm BC.
Bài 11. Cho tứ giác ABCD và điểm O nằm trong tứ giác. Hãy dựng hình bình hành có tâm là O và bốn đỉnh nằm trên bốn cạnh kéo dài của tứ giác.
Bài 12. Cho hai đường tròn ($O_{1}$), ($O_{2}$) và một điểm I. Hãy tìm trên mỗi đường hai điểm sao cho bốn điểm phải tìm là bốn đỉnh của một hình bình hành có tâm là I.
Bài 13. Cho hình vuông ABCD và một điểm K nằm bên trong không trùng với tâm của hình vuông. Dựng qua K một đường thẳng sao cho nó cắt hình vuông thành hai phần có hiệu diện tích lớn nhất.
Bài 14. Cho $\Delta$ABC. Dựng đường thẳng (d) qua A sao cho với mọi điểm M thuộc (d), ta luôn có chu vi $\Delta$MBC lớn hơn hoặc bằng chu vi $\Delta$ABC.
Bài 15. Cho góc nhọn xOy và hai điểm A, B ở trong góc đó. Hãy dựng các điểm C và D lần lượt trên Ox, Oy sao cho đường gấp khúc ABCD có độ dài lớn nhất.
Bài 16. Xác định phương trình đường thẳng ($d_{1}$) đối xứng với đường thẳng (d) qua điểm I, biết:
a. (d): 2x - y + 4 = 0 qua điểm I(-2; 1).
b. (d): x - 2y - 5 = 0 qua điểm I(2; 1).
c. (d): x - 2y + 2 = 0 qua điểm I(1; 1).
Bài 17. Cho hình bình hành ABCD biết phương trình các cạnh (AB): x + 2y - 7 = 0, (AD): x - y + 2 = 0 và tâm I(1; 1). Lập phương trình các cạnh BC và CD.
Bài 18. Xác định phương trình đường tròn ($C_{1}$) đối xứng với đường tròn (C) qua điểm E, biết:
a. (C): $x^{2}$ + $y^{2}$ - 2x - 2y - 2 = 0 và B(2; -3).
b. (C): $x^{2}$ + $y^{2}$ + 4x - 6y + 4 =0 và E(-1; 2).
Bài 19. Cho hàm số:
.png)
Chứng minh rằng đồ thị hàm số nhận điểm .png) làm tâm đối xứng.
làm tâm đối xứng.
Bài 20. Cho hàm số:
.png)
Tìm m để đồ thị hàm số nhận điểm I(2; 3) làm tâm đối xứng.
