Phép vị tự

§7. PHÉP VỊ TỰ

A. TÓM TẮT LÍ THUYẾT

5. ĐỊNH NGHĨA

Định nghĩa: Cho một điểm O cố định và một số k không đổi k $\neq$ 0. Phép biến hình biến mỗi điểm M thành điểm M' sao cho $\overrightarrow{OM'}$ = k$\overrightarrow{OM}$ được gọi là phép vị tự tâm O, tỉ số k.

Ký hiệu là $V_{O}^{k}$ hoặc $V_{(O,k)}$:

6. CÁC TÍNH CHẤT CỦA PHÉP VỊ TỰ

Định lí 1: Nếu phép vị tự tỉ số k biến hai điểm M và N thành hai điểm M' và N' thì:

$\overrightarrow{M'N'}$ = k$\overrightarrow{MN}$ và M'N' = $\mid$k$\mid$ MN.

Định lí 2: Phép vị tự biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm thẳng hàng đó.

Hệ quả: Phép vị tự vị tự tỉ số k:

• Biến đường thẳng thàng đường thẳng song song (hoặc trùng) với đường thẳng đó.

• Biến tia thành tia.

• Biến đoạn thẳng thành đoạn thẳng và độ dài được nhân lên với $\mid$k$\mid$.

• Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là $\mid$k$\mid$.

• Biến góc thành góc bằng nó.

7. ẢNH CỦA ĐƯỜNG TRÒN QUA PHÉP VỊ TỰ

Định lí 3: Phép vị tự tỉ số k biến đường tròn bán kính R thành đường tròn có bán kính $\mid$k$\mid$ R.

8. TÂM VỊ TỰ CỦA HAI ĐƯỜNG TRÒN

Cho hai đường tròn ($I_{1}$; $R_{1}$) và ($I_{2}$; $R_{2}$); với $R_{1}$ $\neq$ $R_{2}$. Có hai phép vị tự $V_{O_{1}}^{k}$ và $V_{O_{2}}^{k}$ biến ($I_{1}$; $R_{1}$) thành ($I_{2}$; $R_{2}$).

Hai tâm vị tự $O_{1}$, $O_{2}$ và tỉ số k được xác định như sau:

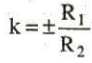• (k > 0 thì gọi là tâm vị tự ngoài, k < 0 thì gọi là tâm vị tự trong).

• $O_{1}$, $O_{2}$ ở trên đường thẳng $I_{1}I_{2}$ và

B. PHƯƠNG PHÁP GIẢI TOÁN

Bài toán 1: Tìm phép vị tự biến hình ($H_{1}$) thành ($H_{2}$).

PHƯƠNG PHÁP CHUNG

Sử dụng định nghĩa và tính chất của phép vị tự.

Ví dụ 1: Cho hình thang ABCD có các đáy CD = 3AB. Hãy xác định các phép vị tự biến $\overrightarrow{AB}$ thành $\overrightarrow{DC}$; biến $\overrightarrow{AB}$ thành $\overrightarrow{CD}$.

Giải

a. Gọi I là giao điểm của AD và BC, khi đó:

b. Gọi O là giao điểm của AC và BD, khi đó:

Ví dụ 2: Xác định tâm vị tự trong và tâm vị tự ngoài của hai đường tròn trong các trường hợp sau:

a. Hai đường tròn tiếp xúc ngoài với nhau.

b. Hai đường tròn tiếp xúc trong với nhau.

c. Một đường tròn chứa đường tròn kia.

Giải

a. Hai đường tròn (I; R) và (I'; R') tiếp xúc ngoài với nhau, ta xét:

Trường hợp 1:

Nếu R = R' thì .

Khi đó, tâm vị tự O thoả mãn:

$\overrightarrow{OI'}$ = k$\overrightarrow{OI}$ ⇒ k chỉ có thể bằng -1

⇒ O (tâm vị tự trong) là trung điểm của II' (chính là tiếp điểm của hai đường tròn)

Trường hợp 2:

Nếu R $\neq$ R' thì ta có thể xác định các phép vị tự sau:

• Lấy A'B' là một đường kính của đường tròn (I'; R') và IA là một bán kính của (I; R) sao cho hai vectơ $\overrightarrow{IA}$ và $\overrightarrow{I'A'}$ cùng hướng.

• Đường thẳng II' cắt AA' và AB' lần lượt tại $O_{1}$ (tâm vị tự ngoài) và $O_{2}$ (tâm vị tự trong và $O_{2}$ trùng với tiếp điểm).

b.

Hai đường tròn (I; R) và (I'; R') tiếp xúc trong với nhau (R $\neq$ R'), ta có thể xác định các phép vị tự sau:

• Lấy A'B' là một đường kính của đường tròn (I'; R') và IA là một bán kính của (I; R) sao cho hai vectơ $\overrightarrow{IA}$ và $\overrightarrow{I'A'}$ cùng hướng.

• Đường thẳng II' cắt AA' và AB' lần lượt tại $O_{1}$ (tâm vị tự ngoài) và $O_{2}$ (tâm vị tự trong).

c.

Đường tròn (I; R) nằm trong đường tròn (I'; R'), ta xét:

Trường hợp 1: Nếu I $\equiv$ I' thì khi đó tâm vị tự O trùng với điểm I.

Vậy, ta có hai phép vị tự:

• Phép vị tự $V_{1}$(I; $k_{1}$) với (biến điểm M thành điểm $M'_{1}$).

• Phép vị tự $V_{2}$(I; $k_{2}$) với (biến điểm M thành điểm $M'_{2}$).

Trường hợp 2: Nếu I không trùng với I' thì ta có thể xác định các phép vị tự sau:

• Lấy A'B' là một đường kính của đường tròn (I'; R') và IA là một bán kính của (I; R) sao cho hai vectơ $\overrightarrow{IA}$ và $\overrightarrow{I'A'}$ cùng hướng.

• Đường thẳng II' cắt AA' và AB' lần lượt tại $O_{1}$ (tâm vị tự ngoài) và $O_{2}$ (tâm vị tự trong).

Bài toán 2: Chứng minh tính chất hình học.

PHƯƠNG PHÁP CHUNG

1. Với bài toán định tính, ta thường gặp các dạng yêu cầu sau:

Dạng 1: Chứng minh ($H_{1}$) là ảnh của ($H_{2}$) qua phép vị tự $V_{O}^{k}$, ta thực hiện theo các bước:

Bước 1: Lấy điểm $M_{1}$ tuỳ ý thuộc ($H_{1}$), ta đi chứng minh $M_{2}$ = $V_{O}^{k}$($M_{1}$) $\in$ ($H_{2}$).

Bước 2: Ngược lại, lấy điểm $M_{2}$ tuỳ ý thuộc ($H_{2}$), ta đi chứng minh $M_{1}$ = $V_{O}^{k}$ ($M_{2}$) $\in$ ($H_{1}$).

Dạng 2: Chứng minh tính chất K, ta thực hiện theo các bước:

Bước 1: Xác định một hoặc nhiều phép vị tự để thiết lập mối liên kết giữa các yếu tố.

Bước 2: Sử dụng các tính chất của phép vị tự để giải các yêu cầu của bài toán.

2. Với bài toán định lượng, bằng việc thiết lập được các phép vị tự thích hợp, ta có thể tính toán được các yếu tố trong một hình.

Ví dụ 1: Cho hai đường tròn (O) và (O') có bán kính khác nhau, tiếp xúc ngoài với (O) và (O') lần lượt tại B và C. Chứng minh rằng đường thẳng BC luôn đi qua một điểm cố định.

Giải

Giả sử đường thẳng BC cắt (O), (O') và OO' theo thứ tự tại A, A' và I.

Vì C tâm vị tự trong của (O') và (O'') nên:

⇒ I là tâm vị tự ngoài của hai đường tròn (O; R) và (O'; R').

Vậy, đường thẳng BC luôn đi qua một điểm cố định là tâm vị tự ngoài của hai đường tròn (O; R) và (O'; R').

Ví dụ 2: Cho đường tròn (O; R) đường kính AB. Một đường tròn (O') tiếp xúc với (O) và đoạn AB lần lượt tại C, D, cắt đường thẳng CD và (O; R) tại I. Tính độ dài các đoạn thẳng AI và BI.

Giải

Ta có:

• C là tâm vị tự dương của hai đường tròn (O) và (O').

• D $\in$ (O'), I $\in$ (O) và ba điểm C, D, I thẳng hàng

Do đó thực hiện phép vị tự tâm C, tỉ số (với R' là bán kính của (O')), ta có:

⇒ I là trung điểm của cung AB ⇒ AI = BI.

Khi đó:

Bài toán 3: Tìm tập hợp điểm M.

PHƯƠNG PHÁP CHUNG

Ta thực hiện theo các bước:

Bước 1: Tìm một phép vị tự $V_{O}^{k}$ biến điểm E di động thành điểm M.

Bước 2: Tìm tập hợp (H) của các điểm E.

Bước 3: Kết luận tập hợp các điểm M là ảnh của (H) trong phép vị tự $V_{O}^{k}$.

Ví dụ 1: Cho hai điểm A và đường thẳng d cố định. M là điểm di động trên d, tìm tập hợp trung điểm của đoạn AM.

Giải

Gọi P là trung điểm của đoạn AM, ta có

Tập hợp các điểm M là đường thẳng d. vậy tập hợp các điểm P là đường thẳng d' ảnh của d trong

Ví dụ 2: Trên đường tròn (C) tâm O bán kính R, cho hai điểm cố định A, B và một điểm M di động. Tìm tập hợp trọng tâm G của tam giác ABM.

Giải

Gọi I là trung điểm của AB, ta có:

Suy ra tập hợp các điểm G là ảnh (C') của (C) trong

Dựng (C'):

• Dựng O' sao cho 3$\overrightarrow{IO'}$ = $\overrightarrow{IO}$

• (C') là đường tròn tâm O' bán kính $\large \frac{R}{3}$.

Ví dụ 3: Cho đường tròn (O, R) và một điểm A cố định ở trên đường tròn; BC là một dây cung di động của đường tròn này và BC có độ dài không đổi bằng 2d (d < R). Tìm tập hợp trọng tâm G của $\Delta$ABC.

Giải

Gọi M là trung điểm cạnh BC thì OM $\perp$ BC.

Trong $\Delta$OMC ta có:

Vậy tập hợp điểm M là đườg tròn ($\gamma$) tâm O bán kính

Suy ra tập hợp các điểm G là đường tròn (C') với

Bài toán 4: Dựng hình.

PHƯƠNG PHÁP CHUNG

Ta luôn thực hiện theo 4 bước đã biết.

Ví dụ 1: Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Hãy dựng qua A một đường thẳng d cắt (O) ở M và cắt (O') ở N sao cho M là trung điểm của AN.

Giải

Phân tích: Giả sử đã dựng được đường thẳng d cắt (O) ở M và cắt (O') ở N sao cho M là trung điểm của AN, gọi Thực hiện phép vị tự V tâm A, tỉ số k = 2 thì N = V(M).

Cách dựng: Ta lần lượt thực hiện:

- Dựng (O") = V(O), khi đó (O'') $\cap$ (O') = {N}.

- Nối AN cắt (O) tại M.

AN là đường thẳng d phải dựng

Chứng minh: Ta có ngay M, N theo thứ tự thuộc đường tròn (O) và (O'), ngoài ra:

N = V(M) ⇒ $\overrightarrow{AN}$ = 2 $\overrightarrow{AM}$

⇒ M là trung điểm của AN.

Biện luận: Vì (O'') cắt (O') tại duy nhất một điểm N nên bài toán chỉ có một nghiệm hình.

Ví dụ 2: Dựng hình vuông nội tiếp trong một tam giác cho trước (hình vuông nội tiếp tam giác là hình vuông có hai đỉnh ở trên một cạnh, hai đỉnh còn lại ở trên hai cạnh còn lại của tam giác)

Giải

Phân tích: Giả sử đã dựng được hình vuông MNPQ nội tiếp trong tam giác ABC cho trước.

Gọi Thực hiện phép vị tự tâm A, tỉ số k thì hình vuông MNPQ sẽ biến thành hình vuông BCDE. Suy ra A, P, D thẳng hàng và A, Q, E thẳng hàng.

Cách dựng: Ta lần lượt thực hiện:

- Dựng hình vuông BCDE sao cho BCDE và ABC nằm ở hai bên của đường thẳng BC.

- AD cắt cạnh BC tại P; AE cắt cạnh BC tại Q .

- Dựng đường thẳng qua P, song song với BC cắt cạnh AC tại N

- Dựng đường thẳng qua N, song song với BC cắt cạnh AB tại M

Thì MNPQ là hình vuông phải dựng

Chứng minh: Theo cách dựng ta có tứ giác MNPQ nội tiếp trong tam giác ABC.

Áp dụng định lý Talet, ta có:

do đó:

$V_{A}^{k}$: MNPQ $\mapsto$ BCDE

mà BCDE là hình vuông nên MNPQ là hình vuông

Biện luận: Ta luôn chỉ có một hình vuông BCDE ở khác phía của tam giác ABC đối với đường thẳng BC nên luôn có chỉ một điểm P và chỉ một điểm Q ở trên cạnh BC.

Vậy bài toán có một và chỉ một nghiệm hình.

BÀI TẬP ĐỀ NGHỊ

Bài 1. Các khẳng định sau đây có đúng không?

a. Phép vị tự luôn có điểm bất động (tức là điểm biến thành chính nó).

b. Phép vị tự không có thể có quá một điểm bất động.

c. Nếu phép vị tự có hai điểm bất động phân biệt thì mọi điểm đều bất động.

Bài 2. Với $\Delta$ABC có hai đỉnh B, C cố định còn đỉnh A chạy trên đường tròn (O; R) cố định không có điểm chung với đường thẳng BC. Chứng tỏ rằng trọng tâm G của $\Delta$ABC là đường tròn (O'; R') là ảnh của đường tròn (O; R) tâm I (I là trung điểm của BC) tỉ số

Bài 3. Với $\Delta$ABC có trọng tâm G, trực tâm H và tâm đường tròn ngoại tiếp O. Chứng minh rằng ba điểm G, H, O thẳng hằng (được gọi là đường thẳng Ơ-le).

Bài 4. Cho hình thang ABCD có các đáy CD = 3AB. Hãy xác định phép vị tự biến $\overrightarrow{AB}$ thành $\overrightarrow{CD}$.

Bài 5. Cho hai đường tròn (O) và ($O_{1}$) có bán kính lần lượt là R và 3R tiếp xúc trong với nhau tại A. Nếu (O) biến thành ($O_{1}$) trong phép vị tự tâm A thì tỉ số vị tự là bao nhiêu?

Bài 6. Cho đường tròn (O) và một điểm I ở ngoài hình tròn (O). Gọi (O') là ảnh của (O) trong Chứng minh rằng I là giao điểm các tiếp tuyến chung của hai đường tròn (O) và (O').

Bài 7. Cho hai điểm B, C cố định thuộc đường tròn (O,R) và điểm A chạy trên đường tròn này. CMR: trọng tâm G của $\Delta$ABC nằm trên một đường tròn. Xác định tâm và bán kính của đường tròn này.

Bài 8. Trên cạnh BC của $\Delta$ABC, lấy hai điểm M, N sao cho BM = CN. Qua M và N lần lượt vẽ các đường thẳng song song với AB, AC. Chứng minh giao điểm của hai đường thằng này nằm trên trung tuyến qua A của $\Delta$ABC.

Bài 9. Cho $\Delta$ABC và một đường thẳng song song với BC cắt các cạnh AB, AC lần lượt tại M và N. Chứng minh rằng các đường tròn (AMN) và (ABC) tiếp xúc nhau.

Bài 10. Cho $\Delta$ABC có A', B', C' lần lượt là trung điểm các cạnh BC, CA, AB. Gọi A'x, B'y, C'z theo thứ tự là các đường thẳng song song với các đường phân giác trong của các góc A, B, C trong tam giác ABC. Chứng minh rằng A'x, B'y, C'z đồng quy.

Bài 11. Cho ba đường tròn ($O_{1}$), ($O_{2}$), ($O_{3}$) đôi một tiếp xúc ngoài tại A, B, C. dây AC kéo dài của ($O_{1}$) gặp ($O_{3}$) tại $A_{1}$. Vẽ đường kính $A_{1}A_{2}$ của ($O_{3}$). Chứng minh rằng A, B, $A_{2}$ thẳng hàng.

Bài 12. Cho tứ giác ABCD có I và J lần lượt là trung điểm của hai cạnh đối AB và CD. Gọi M, N là trung điểm của các đường chéo của tứ giác AIJD; P, Q là trung điểm các đường chéo của tứ giác BIJC. Chứng minh rằng: hoặc 4 điểm M, N, P, Q cùng nằm trên một đường thẳng hoặc chúng tạo thành một hình bình hành.

Bài 13. M, N, P là trung điểm ba cạnh BC, CA, AB của tam giác ABC; H, G, O lần lượt là trực tâm, trọng tâm và tâm đường tròn ngoại tiếp của tam giác ABC, I là tâm đường tròn (MNP).

a. Chứng minh tam giác MNP là ảnh của tam giác ABC trong phép vị tự tâm G, tỉ số -$\large \frac{1}{2}$. Từ đó suy ra 4 điểm O, G, I, H thẳng hàng và I là trung điểm đoạn OH.

b. Chứng minh rằng phép vị tự tâm H, tỉ số $\large \frac{1}{2}$ biến đường tròn (ABC) thành đường tròn (MNP). Từ đó suy ra, trong một tam giác, trung điểm 3 cạnh, chân 3 đường cao và trung điểm các đoạn nối trực tâm với 3 đỉnh là 9 điểm cùng ở trên một đường tròn.

Bài 14. Cho đường tròn (O) và một điểm P cố định. Một cát tuyến di động qua P cắt (O) tại M và N. Gọi I là trung điểm của MN. Tìm tập hợp các trung điểm của IP.

Bài 15. Cho hai đường tròn (O) và (O') tiếp xúc nhau tại A. Đường kính vẽ từ A gặp (O) tại B và (O') tại C. Một đường thẳng di động qua A gặp (O) tại M và (O') tại N. Tìm tập giao điểm của BN và CM.

Bài 16. Cho đường tròn (O, R) và một điểm I cố định với OI = 2R; M là điểm di động trên (O), phân giác của góc IOM cắt IM tại $M_{1}$. Tìm tập hợp các điểm $M_{1}$.

Bài 17. Cho tứ giác ABCD có A, B, C cố định và D di động sao cho AD = l (l > 0)

a. Tìm tập hợp trung điểm của đường chéo BD.

b. Tìm tập hợp các trung điểm M của đoạn nối trung điểm hai đường chéo AC và BD

Bài 18. Cho hình thang ABCD (AB//CD) có A, B cố định, C, D di động sao cho AD = a, CD = b (a, b là hằng số dương). Đặt AB = d, các đường chéo cắt nhau tại I.

a. Tìm tập hợp các điểm C

b. Tìm tập hợp các điểm I

Bài 19. Cho đường tròn (O) và một điểm A ở ngoài đường tròn. Từ A kẻ một tiếp tuyến AB của một đường tròn (B là tiếp điểm) và một cát tuyến di động AMN. Tìm tập hợp trọng tâm G của tam giác BMN.

Bài 20. Cho $\Delta$ABC và một điểm O. Dựng ảnh của $\Delta$ABC qua phép vị tự tâm O với tỉ số:

a. k = 1.

b. k = 2.

c. k = -1.

Bài 21. Dựng hình vuông nội tiếp trong một tam giác cho trước. (Hình vuông nội tiếp trong tam giác là hình vuông có hai đỉnh nằm trên một cạnh, hai đỉnh còn lại nằm trên hai cạnh còn lại).

Bài 22. Dựng đường tròn qua điểm A cho trước, tiếp xúc với hai đường thẳng Ox và Oy cho trước. (Điểm A không ở trên Ox hay Oy).

Bài 23. Cho góc nhọn xOy và một điểm A ở trong góc đó. Hãy dựng một đường tròn đi qua A và tiếp xúc với hai tia Ox và Oy.

Bài 24. Cho $\Delta$ABC nhọn. Dựng hình vuông có hai đỉnh nằm trên cạnh đáy BC và hai đỉnh còn lại nằm trên hai cạnh AB và AC (gọi hình vuông nội tiếp một tam giác cho trước).

Bài 25. Trong một đường mặt phẳng đã cho, hãy dựng một dây cung sao cho các giao điểm của nó với bán kính cho trước không nằm trên một đường thẳng, chia nó thành ba đoạn thẳng bằng nhau.

Bài 26. Dựng tam giác ABC biết $\widehat{A}$ = $\alpha$ và độ dài trung tuyến BM = m, CN = n.

Bài 27. Dựng tam giác ABC biết $\widehat{A}$ = $\alpha$, $\large \frac{AB}{AC}$ = k và độ dài trung tuyến AM = m ($\alpha$, k, m cho trước).

Bài 28. Dựng đường tròn (O) qua A cho trước và tiếp xúc với hai đường thẳng cắt nhau ($d_{1}$), ($d_{2}$) cho trước.

Bài 29. Cho hai đường tròn cắt nhau (O) và (O'). Gọi A là một giao điểm. Hãy dựng một đường thẳng qua A cắt (O) tại M và (O') tại N sao cho AM = 2AN.

Bài 30. Cho đường tròn (O) và đường thẳng (d) không có điểm chung với (O), A là một điểm trên (d). Hãy dựng đường tròn ($\gamma$) tiếp xúc với (O) và tiếp xúc với (d) tại A.