II. BÀI TẬP TỔNG HỢP
Bài 1: Cho lăng trụ đứng tam giác đều \[ABC.{A}'{B}'{C}'\]cạnh đáy bằng a. Gọi M, N và E theo thứ tự là trung điểm của \[BC,C{C}'\]và\[{C}'{A}'\]. Đường thẳng EN cắt đường thẳng AC tại F, đường thẳng MN cắt đường thẳng \[{B}'{C}'\]tại L. FM kéo dài cắt AB tại I, LE kéo dài cắt \[{A}'{B}'\] tại J.
a) Chứng minh rằng các hình đa diện \[IBM.J{B}'L\] và \[{A}'EJ.AFI\] là những hình chóp cụt.
b) Tính thể tích hình chóp\[F.AIJ{A}'\] .
c) Chứng minh rằng mặt phẳng (MNE) chia khối lăng trụ đã cho thành hai khối đa diện có thể tích bằng nhau.
Giải
a) Gọi S là giao của hai đường thẳng MN và\[B{B}'\]. Khi đó S, I, J là điểm chung của hai mặt phẳng (\[MNE\] ) và (ABB'A') nên chúng phải thẳng hàng. Do đó: BB', CC' và IJ đồng quy.
Đa diện \[IBM.J{B}'L\] có hai mặt (IBM) và (\[J{B}'L\]) song song, các cạnh \[B{B}',C{C}'\]và IJ đồng quy nên nó là một hình chóp cụt. Tương tự đa diện \[{A}'EJ.AFI\] cũng là một hình chóp cụt.
b)
.png)
Xét hai tam giác NCF và $N{C}'E$ có:
\[\widehat{C}=\widehat{{{C}'}}=90{}^\circ ,\text{ }NC=N{C}',\text{ }\widehat{CNF}=\widehat{C'NE}\Rightarrow \Delta NCF=\Delta NC'E\].
Do đó: CF = CE = $\frac{a}{2}$
Tương tự \[{C}'L=CM=\frac{a}{2}\]
$\Rightarrow \Delta MCF$ cân ở C và\[\widehat{CMF\text{ }}=\widehat{BMI}=30{}^\circ .\]
Để ý rằng \[\widehat{IBM}\]= 60° nên \[\widehat{MIB}\]= 90°, \[IB=\frac{BM}{2}=\frac{a}{2}\] và $IM=\frac{\sqrt{3}}{2}BM=\frac{\sqrt{3}}{4}a$
Vì \[FI\bot AB,\text{ }FI\bot AA'\] nên \[FI\bot \left( AIJ{A}' \right)\]
Diện tích hình thang vuông \[A{A}'JI\] là: ${{S}_{A{A}'JI}}=\frac{1}{2}\left( \frac{3a}{4}+\frac{a}{4} \right).b=\frac{ab}{2}$ .
Gọi K là trung điểm của MF. Do \[\Delta MCF\] cân ở C nên \[CK\bot MF\Rightarrow \Delta \] vuông CMK = $\Delta $ vuông BMI. Do đó MF = MK = MI.
Từ đó suy ra \[FI\text{ =}\frac{3\sqrt{3}}{4}a\] .
Vậy ${{V}_{F.AIJ{A}'}}=\frac{1}{3}.\left( \frac{ab}{2} \right).\frac{3\sqrt{3}}{4}a=\frac{\sqrt{3}}{8}{{a}^{2}}b$
c) Lý luận như ở câu b, ta có ${C}'L=CM=\frac{a}{2},\,\,LJ\bot {A}'{B}'$ và $LJ=\frac{3\sqrt{3}}{4}a$
Giả sử (MNE) chia khối lăng trụ đã cho thành hai khối đa diện H và (\[{H}'\]) trong đó (H) là khối đa diện chứa đỉnh A, (\[{H}'\]) là khối đa diện chưa đỉnh \[{B}'\].
Ta thấy: ${{V}_{({H}')}}={{V}_{IBM.J{B}'L}}-{{V}_{N.E{C}'L}}$
\[{{V}_{\left( H \right)}}={{V}_{J{A}'E\text{ I}AP}}-{{V}_{N\text{ }FCM}}\]
Vì\[\Delta IBM=\Delta J{A}'E\] , \[\Delta J{B}'L\text{ }=\Delta J{A}'F,\text{ }BB'=A{A}'\] nên\[{{V}_{IBM.J{B}'L}}={{V}_{J{A}'EIAF}}\].
Mặt khác: hai hình chóp \[N.E{C}'L\] và \[N.{F}'CM\] có đáy là những tam giác bằng nhau và có đường cao bằng nhau nên chúng có thể tích bằng nhau.
Vậy \[{{V}_{\left( H \right)}}={{V}_{\left( {{H}'} \right)}}\]
Bài 2: Cho khối chóp S.ABC có đường cao SA bằng 2a, tam giác ABC vuông ở C có cạnh huyền AB = 2a, \[\widehat{CAB}=30{}^\circ .\] Gọi H và K lần lượt là hình chiếu của A trên SC và SB.
a) Tính thể tích khối chóp H.ABC.
b) Chứng minh rằng \[AH\bot SB\] và \[SB\bot \left( AHK \right).\]
c) Tính thể tích khối chóp S.AHK ,
Giải
.png)
a) Trong mặt phẳng (SAC), hạ \[HI\bot AC.\text{ }\Rightarrow HI\bot \left( ABC \right)\]
Ta có: ${{V}_{H.ABC}}=\frac{1}{3}{{S}_{ABC}}.HI$
\[CA=AB.\text{ c}os\text{ }30{}^\circ =a\sqrt{3}\] .
Vậy \[{{S}_{ABC}}=\frac{1}{2}AB.AC.\text{ }sin30{}^\circ \]
$=\frac{1}{2}.2a.2a.cos30{}^\circ .\sin 30{}^\circ =\frac{{{a}^{2}}\sqrt{3}}{2}$
Ta có: $\frac{HI}{SA}=\frac{HC}{SC}=\frac{HC.SC}{S{{C}^{2}}}=\frac{A{{C}^{2}}}{S{{C}^{2}}}=\frac{A{{C}^{2}}}{S{{A}^{2}}+A{{C}^{2}}}$
$=\frac{4{{a}^{2}}.co{{s}^{2}}30{}^\circ }{4{{a}^{2}}+4{{a}^{2}}.co{{s}^{2}}30{}^\circ }=\frac{3}{7}\Rightarrow HI=\frac{6}{7}a$
Vậy ${{V}_{H.ABC}}=\frac{1}{3}{{S}_{ABC}}.HI=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{3}}{2}.\frac{6}{7}a=\frac{{{a}^{3}}\sqrt{3}}{7}$
(Ngoài ra, còn có thể tính${{V}_{H.ABC}}={{V}_{B.AHC}}=\frac{1}{3}{{S}_{AHC}}.BC$).
b) Ta có: \[AH\bot SC,\text{ }AH\bot CB\] (do CB $\bot $ (SAO) $\Rightarrow AH\bot $ (SBC)$\Rightarrow AH\bot SB$ .
Ta có: \[SB\bot AK,\text{ }SB\bot AH\] (do \[AH\bot \] (SBC) suy ra \[SB\bot \] (AHK).
c) Tam giác SAB cân ở A nên\[SK=\frac{1}{2}SB\] $\frac{{{V}_{S.AHK}}}{{{V}_{S.ABC}}}=\frac{SA}{SA}.\frac{SH}{SB}.\frac{SK}{SC}=\frac{1}{2}.\frac{SH}{SC}=\frac{1}{2}\frac{SH.SC}{S{{C}^{2}}}=\frac{1}{2}.\frac{S{{A}^{2}}}{S{{A}^{2}}+S{{C}^{2}}}$
$=\frac{1}{2}.\frac{4{{a}^{2}}}{4{{a}^{2}}+4{{a}^{2}}.co{{s}^{2}}30{}^\circ }=\frac{2}{7}$
${{V}_{S.ABC}}=\frac{1}{3}{{S}_{ABC}}.SA=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{3}}{2}.2a=\frac{{{a}^{3}}\sqrt{3}}{3}$
Vậy \[{{V}_{S.AHK}}=\frac{{{a}^{3}}\sqrt{3}}{3}.\frac{2}{7}=\frac{2{{a}^{3}}\sqrt{3}}{21}\]
Bài 3: Cho hình lăng trụ đứng \[ABC.{A}'{B}'{C}'\] có mặt đáy là tam giác ABC vuông tại B và AB = a, BC = 2a, AA' = 3a. Một mặt phẳng (P) qua A và vuông góc với CA’ lần lượt cắt các đoạn thẳng CC’ và BB' tại M và N.
a) Tính thể tích khối chóp C.A'AB.
b) Chứng minh rằng AN$\bot $ AB.
c) Tính thể tích khối tứ diện\[{A}'AMN\] .
d) Tính diện tích tam giác AMN.
Giải
.png)
a) ${{V}_{C{A}'AB}}={{V}_{{A}'ABC}}=\frac{1}{3}{{S}_{ABC}}.A{A}'=\frac{1}{6}a.2a.3a={{a}^{3}}$
b) Ta có: CB$\bot $ AB, CB$\bot $ AA' (do AA'$\bot $(ABC)
Suy ra CB $\bot $ (A'AB). AA'
Mặt khác: AN$\bot $CA' (do CA$\bot $(AMN))
$\Rightarrow $ AN$\bot $ A'B (theo định lý ba đường vuông góc).
c) Ta có: \[{{V}_{{A}'.AMN}}={{V}_{M.A{A}'N\text{ }}}={{V}_{M.A{A}'B}}\] (vì NB // AA')
$={{V}_{C.A{A}'B}}$ (do MC // (AA'B))
$={{a}^{3}}$
d) ${{S}_{AMN}}=\frac{3.{{V}_{{A}'AMN}}}{{A}'I}=\frac{3{{a}^{3}}}{\frac{3{{a}^{2}}}{\sqrt{{{a}^{2}}+{{(2a)}^{2}}+{{(3a)}^{2}}}}}=\frac{{{a}^{2}}\sqrt{14}}{3}$
Bài 4: Trên ba cạnh của một tam diện vuông đỉnh 0 ta lấy OA = OB = OC = a.
a) Chứng minh rằng ABC là tam giác đều. Tính diện tích toàn phần của tứ diện O.ABC.
b) Tính độ dài đường cao OH hạ từ O xuống mặt phẳng (ABC). Gọi D là điểm đối xứng của H qua O. Chứng minh ABCD là tứ diện đều.
c) Gọi I, J lần lượt là trung điểm của BC và AD. Chứng minh các đoạn IJ và OH cắt nhau tại trung điểm K của mỗi đoạn và IJ là đoạn vuông góc chung của AD và BC. Tính độ dài đoạn IJ.
Giải
.png)
a) Ta có: OA, OB, OC vuông góc với nhau từng đôi một tại O.
Vì ba tam giác vuông cân AOB; BOC; COA bằng nhau, nên ta có AB = BC = CA =$a\sqrt{2}$
Vậy ABC là tam giác đều có cạnh bằng $a\sqrt{2}$
Do đó, ta có diện tích tam giác OAB bằng $\frac{{{a}^{2}}}{2}$ và diện tích tam giác ABC bằng $\frac{{{a}^{2}}\sqrt{3}}{2}$ .
Gọi \[{{S}_{tp}}\]là diện tích toàn phần của tứ diện O.ABC, ta có:
${{S}_{tp}}=\frac{3{{a}^{2}}}{2}+\frac{{{a}^{2}}\sqrt{3}}{2}=\frac{{{a}^{2}}(3+\sqrt{3})}{2}$
b) Gọi H là tâm của tam giác đều ABC, ta có CH = $\frac{a\sqrt{6}}{3}$
Tam giác OHC vuông tại H, ta có:
\[O{{H}^{2}}=O{{C}^{2}}-C{{H}^{2}}=\frac{3{{a}^{2}}}{9}\Rightarrow OH=\frac{a\sqrt{6}}{3}\]
Vì DH$\bot $ (ABC) tại H mà HA = HB = HC nên DA = DB = DC.
Xét tam giác vuông CDH ta có:
$D{{C}^{2}}=D{{H}^{2}}+H{{C}^{2}}=\frac{4{{a}^{2}}}{3}+\frac{2{{a}^{2}}}{3}=2{{a}^{2}}\Rightarrow DC=a\sqrt{2}=AB$
Vậy ABCD là tứ diện đều.
c) Theo giả thiết ta có O và J là trung điểm của DH và AD nên:
JO // AH và JO$=\frac{1}{2}$AH. Do đó JO // HI và JO = HI vì HI $=\frac{1}{2}$ AH.
Vậy tứ giác HIOJ là hình bình hành nên OH và C cắt nhau tại K của mỗi đường.
Tam giác ADI cân tại I vì CÓ AI = ID = $\frac{BC\sqrt{3}}{2}$, nên có IJ$\bot $AD tại trung điểm J của AD. Tương tự tam giác BJC cân đỉnh J nên JI$\bot $BC tại trung điểm I của BC.
Do đó IJ là đường vuông góc chung của AD và BC. Trong tam giác cân ADI, ta có
$IJ=\sqrt{A{{I}^{2}}-A{{J}^{2}}}=\sqrt{{{\left( \frac{a\sqrt{6}}{2} \right)}^{2}}-{{\left( \frac{a\sqrt{2}}{2} \right)}^{2}}}=a$
Bài 5: Cho hai đoạn thẳng AB và CD chéo nhau, BD là đường vuông góc chung của chúng. Biết rằng BD = h, AB = a, CD = b và góc giữa hai đường thẳng AB và CD bằng 60°. Hãy tính thể tích của tứ diện ABCD.
Giải
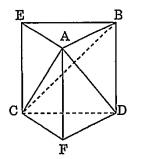
Dựng BE song song và bằng DC; DF song song và bằng BA. Khi đó: ABE.FDC là một lăng trụ đứng.
Ta có: ${{S}_{ABC}}=\frac{1}{2}a.b.\sin 60{}^\circ =\frac{ab\sqrt{3}}{4}$
${{V}_{C.ABE}}=\frac{1}{3}.\frac{\sqrt{3}}{4}.ab.h=\frac{\sqrt{3}}{12}ah$
Từ đó suy ra:\[{{V}_{ABCD}}={{V}_{ANCE}}\text{ }=\frac{\sqrt{3}}{12}abh\]
Bài 6. Cho hình hộp xiên \[ABCD.{A}'{B}'{C}'{D}'\] có tất cả các mặt đều là hình thoi cạnh a. Các góc tại đỉnh A đều bằng α (0° < α < 90°).
a) Chứng minh chân đường cao của lăng trụ vẽ từ A nằm trên đường chéo AC của đáy. Tính thể tích hình hộp.
b) Gọi β là số góc tạo bởi hai mặt phẳng (ABB'A') và (ADD'A'). Tìm sự liên hệ giữa cosα và cosβ.
Giải
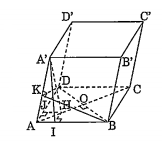
a) Chứng minh hình chiếu của A' lên mp(ABCD) thuộc AC. Ta gọi H, I, J lần lượt là hình chiếu của A' lên mp(ABCD); các đường thẳng AB; AD
Ta có: A'H$\bot $ (ABCD); AB$\bot $A'I; AD$\bot $A'J

Ta có: $\Delta {A}'AI=\Delta {A}'AJ$
Vì AA' chung, và\[\widehat{A'AI}=\widehat{A'AJ}\text{ }=\alpha \] .
Suy ra: AI = AJ = AA'cosα = a.cosα. $\Rightarrow $ HI = HJ. (2) .
Từ (1) và (2) suy ra H ở trên đường phân giác của\[\widehat{BAD}\], tức H$\in $ AC.
* Tính thể tích lăng trụ
Trong tam giác vuông AHI ta có:
$AH=\frac{AI}{cos\frac{\alpha }{2}}=\frac{a.cos\alpha }{cos\frac{\alpha }{2}}$
Trong tam giác vuông AA'H ta có:
${A}'{{H}^{2}}=A{{{A}'}^{2}}-A{{H}^{2}}={{a}^{2}}-\frac{{{a}^{2}}.co{{s}^{2}}\alpha }{co{{s}^{2}}\frac{\alpha }{2}}=\frac{{{a}^{2}}\left( co{{s}^{2}}\frac{\alpha }{2}-co{{s}^{2}}\alpha \right)}{co{{s}^{2}}\frac{\alpha }{2}}$
$\Rightarrow {A}'H=\frac{a}{cos\frac{\alpha }{2}}\sqrt{co{{s}^{2}}\frac{\alpha }{2}-co{{s}^{2}}\alpha }$
• Thể tích hình hộp:
V = \[{{S}_{ABCD}}.{A}'H={{a}^{2}}.\sin \alpha .\frac{a}{\cos \frac{\alpha }{2}}\sqrt{co{{s}^{2}}\frac{\alpha }{2}-co{{s}^{2}}\alpha }=2{{a}^{3}}.\sin \frac{\alpha }{2}\sqrt{co{{s}^{2}}\frac{\alpha }{2}-co{{s}^{2}}\alpha }\] = a’ sin d.
b) Ta có BD$\bot $ AC; BD$\bot $ \[{A}'H\text{ }\Rightarrow \text{ }BD\bot \left( A{A}'{C}'C \right);\]

Suy ra \[\widehat{BKD}\] là góc phẳng tạo bởi hai mặt phẳng (ABB’A’) và (ADD’A’):
Suy ra \[\widehat{BKD}\] = β. Trong tam giác vuông AOB ta có:
OB = AB.sin$\frac{\alpha }{2}=a.\sin \frac{\alpha }{2}\Rightarrow BD=2a.\sin \frac{\alpha }{2}$
Trong tam giác vuông AKB: BK = DK= AB.sinα = a.sinα.
Trong tam giác vuông BDK: BD2 = BK2 + DK2 - 2BK.DK.cosβ
$\Rightarrow 4{{a}^{2}}.{{\sin }^{2}}\frac{\alpha }{2}=2{{a}^{2}}.{{\sin }^{2}}\alpha \left( 1-cos\beta \right)\Rightarrow cos\beta .\sin \frac{\alpha }{2}=\frac{1}{2}$
Bài 7. Cho lăng trụ xiên ABC.A'B'C', đáy là tam giác đều cạnh a và AA' = A'B = A'C = b.
a) Xác định đường cao của lăng trụ vẽ từ A'. Chứng minh mặt bên BCC'B' là hình chữ nhật.
b) Xác định b để mặt bên ABB'A' hợp với mặt đáy góc 60°.
c) Tính thể tích và diện tích toàn phần theo a với giá trị b tìm được ở câu b.
Giải

a) • Xác định đường cao. Vẽ A'H $\bot $ mp(ABC). Ta có AA' = A'B = A'C
$\Rightarrow $ HA = HB = HC
$\Rightarrow $ H là tâm của tam giác đều ABC.
Vậy đường cao vẽ từ A là đoạn nối A với tâm của đường tròn ngoại tiếp tam giác ABC.
• Chứng minh BCC'B' là hình chữ nhật.
Ta có: BC$\bot $ AH;
AH là hình chiếu của AA' lên mặt phẳng (ABC).
Vậy BC$\bot $ AA'
Mà BB // AA' $\Rightarrow $ BC$\bot $ BB' tức là mặt bên BCC'B' là hình chữ nhật.
b) Xác định b theo a.
Gọi J là trung điểm của AB.
Ta thấy \[\widehat{{A}'JH}\] là góc mà mặt bên (ABB'A') hợp với đáy. Trong tam giác vuông A'AJ, ta có:
${A}'J=\sqrt{A{{{{A}'}}^{2}}-A{{J}^{2}}}=\sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{4}}\Rightarrow HJ=\frac{1}{3}CJ=\frac{1}{3}\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}$
Trong tam giác A'JH: \[cos\widehat{\left( ASH \right)}=\frac{HJ}{{A}'J}=\frac{a}{6}\sqrt{\frac{3}{{{b}^{2}}-\frac{{{a}^{2}}}{4}}}\]
Để \[\widehat{A'JH}\] = 60° thì ta phải có: $\frac{a}{6}\sqrt{\frac{3}{{{b}^{2}}-\frac{{{a}^{2}}}{4}}}=\frac{1}{2}\Leftrightarrow b=a\sqrt{\frac{7}{12}}$
c) Thể tích lăng trụ: V = ${{S}_{ABC}}.{A}'H=\frac{{{a}^{2}}\sqrt{3}}{4}.{A}'H$
Trong tam giác vuông A'JH ta có A'H = HJ. tan 60° = $\frac{a\sqrt{3}}{6}.\sqrt{3}=\frac{a}{2}$
Do đó $V=\frac{{{a}^{3}}\sqrt{3}}{8}$ .
• Ta có: ${{S}_{ABC}}={{S}_{{A}'{B}'{C}'}}=\frac{{{a}^{2}}\sqrt{3}}{4}$ (vì A'J = 2HJ = $\frac{a\sqrt{3}}{3}$)
Do BB'C'C là hình chữ nhật $\Rightarrow $ ${{S}_{BC{C}'{B}'}}=BC.B{B}'=ab={{a}^{2}}\sqrt{\frac{7}{12}}=\frac{{{a}^{2}}\sqrt{21}}{6}$
Diện tích toàn phần: ${{S}_{tp}}=2{{S}_{ABC}}+2{{S}_{AB{B}'{A}'}}+{{S}_{BC{C}'{B}'}}=\frac{{{a}^{2}}}{6}\left( 7\sqrt{3}+\sqrt{21} \right)$
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, cạnh SA $\bot $ (ABCD) và có độ dài SA = a. Một mặt phẳng đi qua CD cắt các cạnh SA, SB lần lượt ở M, N đặt AM = x.
a) Tứ giác MNCD là hình gì? Tính diện tích tứ giác MNCD theo a, x.
b) Xác định giá trị của x để thể tích hình chóp S.MNCD bằng $\frac{2}{9}$ lần thể tích hình chóp S.ABCD.
Giải
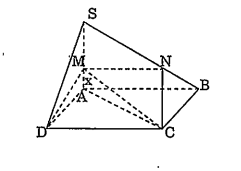
a) Tứ giác MNCD là hình gì?
Mặt phẳng (SAB) và mặt phẳng (MCD) qua hai đường thẳng song song AB và CD lại cắt nhau , nên giao tuyến MN // AB // CD.
Do CD$\bot $AD và SA nên CD$\bot $ (SAD) $\Rightarrow $ CD$\bot $MD và \[\widehat{MDC}\] = 90°.
Mà MN // CD nên MN$\bot $ CD.
Vậy MNCD là hình thang vuông tại M và D.
Ta có dt(MNCD) = $\frac{1}{2}$ (MN+CD).MD.
Biết SA = a, MA = x nên SM = a -x.
$\Delta $SAB đều, $\Delta $SMN cũng là tam giác đều suy ra MN = SM = a - x.
$\Delta $MAD vuông có: MD =$\sqrt{A{{M}^{2}}+A{{D}^{2}}}=\sqrt{{{x}^{2}}+{{a}^{2}}}$.
Do đó: dt(MNCD) =$\frac{1}{2}\left[ \left( a-x \right)+a \right]\sqrt{{{x}^{2}}+{{a}^{2}}}$ $\Rightarrow dt(MNCD)=\frac{2a-x}{2}\sqrt{{{x}^{2}}+{{a}^{2}}}$ .
b) Xác định x để ${{V}_{S.MNCD}}=\frac{2}{9}{{V}_{S.ABCD}}$
Gọi ${{V}_{2}}$ là thể tích hình lăng trụ cụt AMD.BNC có thiết diện phẳng là $\Delta $AMD, ta có:
\[{{V}_{2}}=\frac{MN+AB+CD}{3}dt(AMD)=\frac{\left( a-x \right)+a+a}{3}.\frac{1}{2}ax=\frac{ax}{6}(3a-x)\]
${{V}_{1}}$ là thể tích hình chóp S.MNCD, V là thể tích S.ABCD.
Theo giá thiết $\frac{{{V}_{1}}}{V}=\frac{2}{9}$ nên ${{V}_{2}}=\frac{7}{9}V=\frac{7}{9}.\frac{{{a}^{3}}}{3}$
Do đó: $\frac{ax}{6}(3a-x)=\frac{7{{a}^{3}}}{27}\Leftrightarrow 9{{x}^{2}}-27ax+14=0$
.png)
Vậy khi $x=\frac{2}{3}a$ thì $\frac{{{V}_{1}}}{V}=\frac{{{V}_{SMNCD}}}{{{V}_{SABCD}}}=\frac{2}{9}$
Bài 9. Cho tứ diện ABCD có AB = a, BC = b, BD = c, \[\widehat{ABD}\text{ }=\text{ }\widehat{ABC\text{ }}=\text{ }60{}^\circ ,\] \[\widehat{CBD}\] = 90°
a) Tính thể tích tứ diện ABCD.
b) Tìm điều kiện đối với a,b,c để AB$\bot $ CD
c) Chứng minh rằng nếu \[\widehat{CAD}\] > 90° thì CD > AB
Giải
a) Tính thể tích tứ diện ABCD.
Dựng AM$\bot $BC, AN $\bot $BD và đường cao AH của hình chóp thì BM$\bot $MH và BN$\bot $NH (định lý ba đường vuông góc). Trong $\Delta $AMB vuông góc tại M ta có:
BM = AB.\[\cos \widehat{ABM}=a.cos\text{ }60{}^\circ =\frac{a}{2}\]
AM =\[AB.sin60{}^\circ =\frac{a\sqrt{3}}{2}\] .
Trong $\Delta $BMH vuông góc tại M ta có:
MH = BM.\[tan\text{ }\widehat{MBH}=BM.\tan 45{}^\circ =\frac{a}{2}\]
Xét $\Delta $AHM vuông góc tại H ta có:
AH = VAM – MH$\sqrt{A{{M}^{2}}-M{{H}^{2}}}=\sqrt{{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}-{{\left( \frac{a}{2} \right)}^{2}}}$
$\Rightarrow AH=\frac{a\sqrt{2}}{2}$
Diện tích đáy BCD là dt(BCD) = $\frac{1}{2}$BC.BD = $\frac{1}{2}$bc.
Thể tích hình chóp: V = $\frac{1}{3}$dt($\Delta $BCD).AH = $\frac{1}{3}$.$\frac{1}{2}$bc$\frac{a\sqrt{2}}{2}=\frac{\sqrt{2}abc}{12}$
b) Tìm điều kiện đối với a,b,c để AB$\bot $ CD.
Ta có: CD$\bot $AB (giả thiết).
CD$\bot $AH (AH là đường cao);
$\Rightarrow $ CD$\bot $ (ABH) $\Rightarrow $ CD$\bot $BI.
BI là đường phân giác của \[\widehat{CBD}\] mà BI$\bot $CD nên $\Delta $BCD là tam giác cân hay BC = BD
$\Rightarrow $ b = c.
c) Nếu \[\widehat{CAD}\] > 90° thì CD > AB.
Nếu\[\widehat{CAD}\]> 90° thì hình cầu đường kính CD qua B còn A ở trong hay ở trên hình cầu. Từ đó suy ra khi \[\widehat{CAD}\] > 90° thì CD > AB.
Bài 10. Cho hình chóp tứ giác đều S.ABCD.
a) Biết AB = a, góc giữa mặt bên và đáy bằng α. Tính thể tích và diện tích xung quanh của hình chóp.
b) Biết trung đoạn bằng d và góc giữa cạnh bên và đáy bằng $\varphi $ . Tính thể tích hình chóp.
Giải
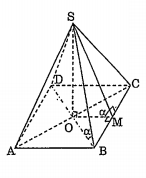
a) S.ABCD là hình chóp tứ giác đều nên ABCD là hình vuông tâm O.
Ta có: SO$\bot $mp(ABCD) với SO là đường cao.
Gọi M là trung điểm của BC, ta có:
.png)
$\Rightarrow SO=OM.\tan \alpha =\frac{a}{2}.\tan \alpha $
Diện tích đáy $S={{a}^{2}}$
Vậy$V=\frac{1}{6}{{a}^{3}}.\tan \alpha $
Ta có trong đoạn SM =$\frac{OM}{cos\alpha }=\frac{a}{2cos\alpha }$
Vậy ${{S}_{xq}}=\frac{1}{2}.4a.\frac{a}{2\cos \alpha }=\frac{a}{2\cos \alpha }$
b) Tính thể tích hình chóp.
Ta có: $SO\bot $ mp(ABCD) $\Rightarrow $ OA là hình chiếu của cạnh bên SA trên mặt đáy $\Rightarrow \widehat{SAO}=\varphi $
Gọi cạnh đáy AB = x $\Rightarrow $ OA =$\frac{x\sqrt{2}}{2}$, OM$=\frac{x}{2}$ .
Trong tam giác vuông SOM: \[S{{O}^{2}}\text{= }S{{M}^{2}}O{{M}^{2}}={{d}^{2}}-\frac{{{x}^{2}}}{4}\] (1)
Trong tam giác vuông SOA: SO = OA$\tan \varphi $ (2)
Từ (1) và (2) suy ra: ${{\left( \frac{x\sqrt{2}}{2}\tan \varphi \right)}^{2}}={{d}^{2}}-\frac{{{x}^{2}}}{4}\Rightarrow \frac{{{x}^{2}}{{\tan }^{2}}\varphi }{2}+\frac{{{x}^{2}}}{4}={{d}^{2}}$
Từ đây ta có: $SO=\frac{x\sqrt{2}}{2}\tan \varphi =\frac{\sqrt{2}.d.\tan \varphi }{\sqrt{1+2{{\tan }^{2}}\varphi }}$
Vậy $V=\frac{1}{3}Bh=\frac{1}{3}{{\left[ \frac{2d}{\sqrt{1+2{{\tan }^{2}}\varphi }} \right]}^{2}}\frac{\sqrt{2}d.\tan \varphi }{\sqrt{1+2{{\tan }^{2}}\varphi }}=\frac{4\sqrt{2}.{{d}^{3}}.\tan \varphi }{3\sqrt{{{\left( 1+2{{\tan }^{2}}\varphi \right)}^{3}}}}$
Bài 11. Cho hình chóp S.ABCD có đáy là hình vuông ABCD tâm O cạnh a, SA$\bot $ mp(ABCD), SA =$a\sqrt{3}$ .
a) Chứng minh hình chóp S.ABCD cô một mặt phẳng đối xứng và các mặt bên của hình chóp đều là tam giác vuông. Tính theo a diện tích toàn phần và thể tích của hình chóp.
b) M là một điểm bất kì trên cạnh SB, đặt BM = x. Mặt phẳng (ADM) cắt BC tại N. Xác định hình dạng các tứ giác AMND và BMNC. Tính diện tích y của tứ giác BMNC theo a và x.
c) Tìm x để mp(ADM) vuông góc với SB. Khi đó hãy tính tỉ số thể tích các phần của hình chóp S.ABCD được chia bởi mp(ADM).
d) Tìm tập hợp giao điểm I của AM và DN khi M vạch đoạn thẳng SB.
Tính z = SI theo a và x. Khảo sát sự biến thiên của z khi M di chuyển trên đoạn SB.
Hướng dẫn
a) mp(SAC) là mặt phẳng đối xứng của hình chóp ${{S}_{tp}}={{a}^{2}}\left( 3+\sqrt{3} \right)$
$V=\frac{{{a}^{3}}\sqrt{3}}{3}$
b)

AMND là hình thang vuông tại A và M. BMNC là hình thang vuông tại B và M.
$y=dt(BMNC)=\frac{1}{2}(BC+MN).BM$
$=-\frac{{{x}^{2}}}{4}+ax$
c) SB$\bot $mp(ADM) $\Rightarrow $ SB$\bot $AM $\Leftrightarrow $ M trùng với chân đường cao H hạ từ A của $\Delta $SAB $\Leftrightarrow x=BH=\frac{B{{A}^{2}}}{BS}=\frac{a}{2}$
Gọi ${{V}_{1}}$ , là thể tích hình chóp S.AHKD và${{V}_{2}}$ , là thể tích phần còn lại (xem hình) ta có: ${{V}_{1}}=\frac{1}{3}dt\left( AHKD \right).SH=\frac{7{{a}^{3}}\sqrt{3}}{32};\,\,{{V}_{2}}={{V}_{S.ABCD}}-{{V}_{1}}=\frac{11{{a}^{3}}\sqrt{3}}{96}$
Do do $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{21}{11}$
d) Tập hợp của I là nửa đường thẳng St song song với AB và nằm trong góc vuông SAB.
$z=SI=\frac{a\left( 2a-x \right)}{x}$ (z là một hàm số bậc nhất theo x, với$x\in (0;2a]$ .
Bài 12: Trong mặt phẳng (P) cho hình chữ nhật ABCD, AB = a, AD = b. Một điểm M chuyển động trên đường tròn (C) đường kính BD trong mặt phẳng (Q) vuông góc với (P), cắt (P) theo giao tuyến BD. Đặt BM = x.
a) Tính thể tích hình chóp M.ABCD theo a, b, x.
b) Chứng minh rằng MAC là tam giác vuông.
c) Tìm quỹ tích hình chiếu vuông góc của A lên đường thẳng MB.
Giải
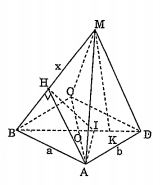
a) Thể tích hình chóp M.ABCD.
Vē MK$\bot $BD. Do mp(MBD) $\bot $mp(ABCD) suy ra MK$\bot $mp(ABCD)
Trong $\Delta $ BMD vuông tại M nên:
$\frac{1}{M{{K}^{2}}}=\frac{1}{M{{B}^{2}}}+\frac{1}{M{{D}^{2}}}=\frac{1}{{{x}^{2}}}+\frac{1}{{{a}^{2}}+{{b}^{2}}-{{x}^{2}}};$
$\frac{1}{M{{K}^{2}}}=\frac{{{a}^{2}}+{{b}^{2}}}{{{x}^{2}}\left( {{a}^{2}}+{{b}^{2}}-{{x}^{2}} \right)};$
$\Rightarrow MK=\frac{x\sqrt{{{a}^{2}}+{{b}^{2}}-{{x}^{2}}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=x\sqrt{1-\frac{{{x}^{2}}}{{{a}^{2}}+{{b}^{2}}}}$ ar x
Gọi V là thể tích hình chóp M.ABCD, ta có:
$V=\frac{1}{3}dt\left( ABCD \right).MK=\frac{1}{3}abx\sqrt{1-\frac{{{x}^{2}}}{{{a}^{2}}+{{b}^{2}}}}$
b) Chứng minh $\Delta $MAC vuông.
Gọi O là giao điểm của hai đường chéo AC và BD. Ta có: OA = OB = OC = OD (1)
M thuộc đường tròn đường kính BD nên OM = OB = OD (2)
Từ (1) và (2) suy ra OM = OA = OC
$\Rightarrow \Delta $MAC vuông tại M.
c) Quỹ tích hình chiếu vuông góc của A lên MB.
Dựng AI$\bot $BD $\Rightarrow $ IA$\bot $ (Q) và IA$\bot $HI.
Theo định lý ba đường vuông góc thì BH$\bot $HI.
Trong mặt phẳng (Q), H nhìn BI cố định dưới một góc vuông nên H nằm trên đường tròn đường kính BI, trừ hai điểm B và I.
Bài 13. Cho hình chữ nhật EFGH. Đường thẳng Et vuông góc với mặt phẳng (EFGH) tại E. Trên Et lấy điểm P. Mặt phẳng qua E vuông góc với PG cắt PF, PG, PH lần lượt tại F’, G’, H’.
a) Chứng minh tứ giác EFGH nội tiếp.
b) Chứng minh mặt phẳng (EFGH) luôn đi qua một đường thẳng cố định khi P chạy trên Et.
c) Gọi α là góc nhọn tạo bởi PG với mặt phẳng (PEF). Hãy tính tỷ số thể tích của hai hình chóp P.EF’G’H’ và P.EFGH khi EFGH là hình vuông.
Giải
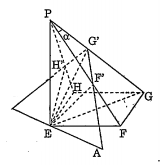
a) Chứng minh tứ giác EF’G’H’ nội tiếp. Biết PG$\bot $(EF'G'H') $\Rightarrow $ PG$\bot $EF' (1)
.png)
.png)
Từ (1) và (2) suy ra EF'$\bot $(PFG) $\Rightarrow $ EF'$\bot $F'G' $\Rightarrow \widehat{E{F}'{G}'}=90{}^\circ $
Tương tự: PG$\bot $EH' (3)
.png)
Từ (3) và (4) ta có: EH'$\bot $(PHG) $\Rightarrow $ EH'$\bot $H'G' $\Rightarrow $$\widehat{E{H}'{G}'}=90{}^\circ $.
Tứ giác EF'G'H' có hai góc đối (H' và F') bù nhau là tứ giác nội tiếp.
b) Chứng minh (EF'G'H') luôn đi qua một đường thẳng cố định.
Mặt thiết diện EF'G'H' và mặt đáy EFGH có chung điểm E nên chúng cắt nhau theo giao tuyến $\Delta $ qua E.
Ta có: $\Delta \bot PE$ (vì $\Delta $ thuộc đáy EFGH);
$\Delta \bot $PG (vì A thuộc thiết diện EF'G'H');
nên $\Delta \bot $(PEG) $\Rightarrow \Delta \bot EG$
Do $\Delta $ là đường thẳng trong mặt phẳng đáy (EFGH) qua E và vuông góc với EG nên $\Delta $ là đường thẳng cố định khi P chạy trên Et. Vậy mp(EF'G'H') luôn đi qua $\Delta $ cố định.
c) Tính tỷ số thể tích hình chóp P.EF'G'H' và P.EFGH.
Vì FG$\bot $EF và FG$\bot $PE nên FG$\bot $(PEF) $\Rightarrow \Delta $PFG vuông tại F.
Do đó góc $\widehat{GPF}$ chính là gốc α hợp bởi PG và mặt phẳng (PEF).
Gọi V là thể tích hình chóp P.EFGH thì:${{V}_{P.EEH}}={{V}_{P.HPG}}=\frac{V}{2}$ .
Tỷ số thể tích của hai hình tứ diện cho ta:
$\frac{{{V}_{P.E{F}'{H}'}}}{{{V}_{P.EFH}}}=\frac{2{{V}_{P.E{F}'{H}'}}}{V}=\frac{P{F}'.P{H}'}{PE.PH}$ (1)
\[\frac{{{V}_{P.{H}'{F}'{G}'}}}{{{V}_{P.HFG}}}=\frac{2VP.{H}'{F}'{G}'}{V}=\frac{P{H}'.P{F}'.P{G}'}{PH.PF.PG}\] (2)
Gọi a là cạnh hình vuông EFGH.
Trong $\Delta $PFG vuông tại F ta có:
PF = FG.cotα = a.cotα = PH. (3)
$PG=\frac{FG}{\sin \alpha }=\frac{a}{\sin \alpha }$ (4)
Trong $\Delta $PEF vuông tại E ta có:
$P{{E}^{2}}=P{{F}^{2}}-E{{F}^{2}}={{a}^{2}}{{\cot }^{2}}\alpha -{{a}^{2}}=\frac{{{a}^{2}}\cos 2\alpha }{{{\sin }^{2}}\alpha }\Rightarrow PE=\frac{a\sqrt{\cos 2\alpha }}{\sin \alpha }$ (5)
Và $P{{E}^{2}}=P{F}'.PF\Rightarrow P{F}'=\frac{P{{E}^{2}}}{PF}=\frac{a\cos 2\alpha }{\sin \alpha \cos \alpha }=P{H}'$ (6)
Trong $\Delta $PEG vuông tại E ta có:$P{{E}^{2}}=P{G}'.PG\Rightarrow P{G}'=\frac{P{{E}^{2}}}{PG}=\frac{a\cos 2\alpha }{\sin \alpha }$
Thay các giá trị ở (3), (4), (5) và (6) vào (1) và (2) ta được:
$\frac{2{{V}_{P.EF{H}'}}}{V}=\frac{\frac{{{a}^{2}}{{\cos }^{2}}2\alpha }{{{\sin }^{2}}\alpha {{\cos }^{2}}\alpha }}{\frac{{{a}^{2}}{{\cos }^{2}}\alpha }{{{\sin }^{2}}\alpha }}=\frac{{{\cos }^{2}}2\alpha }{{{\cos }^{4}}\alpha }$ (7)
$\frac{2{{V}_{P.{H}'{F}'{G}'}}}{V}=\frac{\frac{{{a}^{2}}{{\cos }^{2}}2\alpha }{{{\sin }^{2}}\alpha {{\cos }^{2}}\alpha }.\frac{a\cos 2\alpha }{\sin \alpha }}{\frac{{{a}^{2}}{{\cos }^{2}}\alpha }{{{\sin }^{2}}\alpha }.\frac{a}{\sin \alpha }}=\frac{{{\cos }^{3}}2\alpha }{{{\cos }^{4}}\alpha }$ (8)
Cộng (7) và (8) ta được:
$\frac{2{{V}_{P.E{F}'{G}'{H}'}}}{V}=\frac{co{{s}^{2}}2\alpha \left( 1+\cos 2\alpha \right)}{{{\cos }^{4}}\alpha }=\frac{{{\cos }^{2}}2\alpha }{{{\cos }^{2}}\alpha }$
Bài 14. ABC là tam giác đều cạnh a, tâm O. Trên đường thẳng d vuông góc với mặt phẳng (ABC) tại A, lấy điểm M khác A. Gọi H là trực tâm tam giác MBC, Đường thẳng OH cắt d tại N.
a) Chứng minh OH vuông góc với mặt phẳng (MBC) và tứ diện ACMN có các cặp cạnh đối diện vuông góc với nhau.
b) Gọi P là trung điểm của cạnh BC. Biết MH = 3HI. Hãy tính MN theo a.
c) Xác định vị trí của điểm M trên d để tứ diện ACMN có thể tích nhỏ nhất.
Giải

a) Chứng minh OH$\bot $ mp(MBR).
Gọi I là trung điểm của BC thì AI$\bot $ BC. MI$\bot $BC (do $\Delta $MAC = $\Delta $MAB nên MB = MC) .
$\Rightarrow $ BC$\bot $ mp(MAI) $\Rightarrow $ mp(MAI)$\bot $ mp(MBC).
.png)
$\Rightarrow BC\bot $ mp(MAC) $\Rightarrow $ BO$\bot $ MC. (2)
Trong $\Delta $MBC ta có: BH$\bot $MC. (3)
Từ (2) và (3) suy ra MC$\bot $ (BOH)
$\Rightarrow $ (MBC) $\bot $(BOH). (4)
Từ (1) và (4) $\Rightarrow $giao tuyến của (MAI) và (BOH) cùng vuông góc với (MBC) $\Rightarrow $ OH$\bot $(MBC)
* Tứ diện BCMN có các cặp đối vuông góc với nhau.
Biết MC$\bot $(BOH) mà NB$\subset $(BCH).
Vậy MC$\bot $NB.
.png)
Vậy các cặp cạnh đối của tứ diện vuông góc với nhau.
b) Tính MN theo a.
Biết OH$\bot $(MBC} nên OH$\bot $MI.
Tứ giác $\Delta $OHM có các góc đối vuông là tứ giác nội tiếp được nên ta có: IH.IM = IO.IA (1)
AI là đường cao của tam giác đều nên $IA=\frac{a\sqrt{3}}{2}$ và \[OI=\frac{1}{3}OA=\frac{a\sqrt{3}}{6}\]
Biết MH = 3HI hay $\frac{HI}{MH}=\frac{1}{3}\Rightarrow \frac{HI}{IM}=\frac{1}{4}$ hay IM = 4HI.
Do đó (1) có thể viết. $\frac{1}{4}$ IM.IM $=\left( \frac{1}{3}.\frac{a\sqrt{3}}{2} \right)\left( \frac{a\sqrt{3}}{2} \right)=\frac{{{a}^{2}}}{4}\Rightarrow IM=a$
$\Delta $HAI vuông góc ở A nên : $A{{M}^{2}}=I{{M}^{2}}-A{{I}^{2}}={{a}^{2}}-{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}=\frac{{{a}^{2}}}{4}\Rightarrow AM=\frac{a}{2}$
$\Delta $NAO$\backsim $ $\Delta $IAM ($\Delta $vuông có $\widehat{N}=\widehat{AIM}$) $\Rightarrow \frac{AN}{AI}=\frac{AO}{AM};$
$\Rightarrow AN=\frac{AO.AI}{AM}=\frac{\frac{2}{3}.\frac{a\sqrt{3}}{2}.\frac{a\sqrt{3}}{2}}{\frac{a}{2}}=a$
Vậy MN = AM + AN = $\frac{a}{2}+a=\frac{3a}{2}$
c) Xác định M để tứ diện BCMN đạt thể tích nhỏ nhất.
Gọi V là thể tích tứ diện BCMN, ta có:
$V={{V}_{MABC}}+{{V}_{NABC}}=\frac{1}{3}dt(\Delta ABC)(MA+NA)$
$=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{3}}{4}(MA+NA)\ge \frac{{{a}^{2}}\sqrt{3}}{12}2\sqrt{AM.AN}=\frac{{{a}^{3}}\sqrt{6}}{12}$
Dấu "=" xảy ra khi AM.AN = AOAI = hay MA = AN =$\frac{a\sqrt{2}}{2}$
Vậy khi AM = AN = $\frac{a\sqrt{2}}{2}$ thì tứ diện BCNM có thể tích nhỏ nhất.
Bài 15. Trong mặt phẳng (P) cho hình vuông ABCD cạnh a. Gọi O là giao điểm của hai đường chéo. Trên đường thẳng Ox vuông góc với (P) lấy một điểm S. Gọi α là góc do mặt bên của hình chóp SABCD tạo với đáy.
a) Xác định đường vuông góc chung của SA và CD. Tính độ dài đoạn vuông góc chung đó.
b) Mặt phẳng đi qua AC và vuông góc với mặt bên SAD chia hình chóp thành hai phần. Tính tỷ số thể tích của hai phần đó.
Giải
.png)
a) Xác định đường vuông góc chung của SA và CD.
I và J lần lượt là trung điểm của AB và CD. Dựng .png)
Qua H dựng NE // BA cắt SB tại N và SA tại E. Từ E trong mặt phẳng NECD dựng EF // HJ cắt CD tại F.
.png)
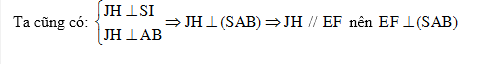
$EF\bot SA$ (2)
Từ (1) và (2) suy ra EF chính là đường vuông góc chung của SA và CD.
Tính EF. Do EFJH là hình chữ nhật đến EF = HJ.
Biết SI$\bot $AB và IJ$\bot $AB nên $\widehat{SIJ}=\alpha $ .
Trong $\Delta $IHJ vuông tại H ta có: JH = EF = \[IJ\sin \alpha =asin\alpha .\]
b) Tính tỷ số thể tích do mặt phẳng qua AC vuông góc với mp(SAD) chia hình chóp thành hai phần.
Biết AC$\bot $BD và AC$\bot $SO nên AC$\bot $(SBD) $\Rightarrow $ AC$\bot $SD.

Trong (SAD) dựng AK$\bot $SD suy ra SD$\bot $ (ACK) $\Rightarrow $ (SAD) $\bot $ (ACK)
(ACK) chính là mặt phẳng qua AC và vuông góc với (SAD).
Mặt phẳng (ACK) chia hình chóp làm hai phần, gọi phần ở dưới mặt ACK là ${{V}_{1}}$, phần ở trên mặt (ACK) là ${{V}_{2}}$.
V là thể tích S.ABC.
.png)
$\Rightarrow \frac{{{V}_{1}}}{V}=\frac{1}{2}.\frac{KI}{SO}=\frac{1}{2}.\frac{KS}{SD}$ (1)
Trong ASD vuông tại J ta có:
$S{{D}^{2}}=S{{J}^{2}}+J{{D}^{2}}={{\left( \frac{a}{2\cos \alpha } \right)}^{2}}+{{\left( \frac{a}{2} \right)}^{2}}=\frac{{{a}^{2}}\left( 1+{{\cos }^{2}}\alpha \right)}{4{{\cos }^{2}}\alpha }\Rightarrow SD=\frac{a\sqrt{1+{{\cos }^{2}}\alpha }}{2\cos \alpha }$
Diện tích $\Delta $SCD: $dt\left( \Delta SCD \right)=\frac{1}{2}CD.SJ=\frac{1}{2}SD.CK$
$\Rightarrow CK=\frac{CD.SJ}{SD}=\frac{a.\frac{a}{2\cos \alpha }}{\frac{a\sqrt{1+{{\cos }^{2}}\alpha }}{2\cos \alpha }}=\frac{a}{\sqrt{1+{{\cos }^{2}}\alpha }}$
Trong $\Delta $CKD vuông tại K ta có:
$D{{K}^{2}}=C{{D}^{2}}-C{{K}^{2}}={{a}^{2}}-\frac{{{a}^{2}}}{1+{{\cos }^{2}}\alpha }=\frac{{{a}^{2}}{{\cos }^{2}}\alpha }{1+{{\cos }^{2}}\alpha }\Rightarrow DK=\frac{a\cos \alpha }{\sqrt{1+{{\cos }^{2}}\alpha }}$ (2)
Thế (2) vào (1) ta có:
$\frac{{{V}_{1}}}{V}=\frac{1}{2}.\frac{\frac{a\cos \alpha }{\sqrt{1+{{\cos }^{2}}\alpha }}}{\frac{a\sqrt{1+{{\cos }^{2}}\alpha }}{2\cos \alpha }}=\frac{{{\cos }^{2}}\alpha }{1+{{\cos }^{2}}\alpha }$
Do đó: \[\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{{{V}_{1}}}{V-{{V}_{1}}}=\frac{\frac{{{V}_{1}}}{V}}{1-\frac{{{V}_{1}}}{V}}=\frac{\frac{{{a}^{2}}{{\cos }^{2}}\alpha }{1+{{\cos }^{2}}\alpha }}{1-\frac{{{\cos }^{2}}\alpha }{1+{{\cos }^{2}}\alpha }}={{\cos }^{2}}\alpha \]
Bài 16. Cho đường tròn (C) có đường kính AB = 2R. Trên nửa đường thẳng Ax vuông góc với mặt phẳng của (O) tại A, lấy điểm E sao cho AS = h. Gọi M là một điểm di động trên (C), mặt phẳng (P) qua A, vuông góc với SB cắt SB và SM lần lượt tại H, K.
a) Chứng minh AK$\bot $(SEM) và điểm K chạy trên một đường tròn cố định khi M thay đổi.
b) Tính thể tích hình chóp SAHK trong trường hợp M là trung điểm của cung AB.
Giải
.png)
a) Chứng minh AK$\bot $mp(SBM).
.png)
Do đó MB$\bot $AK (1)
Biết SB$\bot $(P)
AK$\bot $SB (2)
Từ (1) và (2) suy ra: AK$\bot $(SMB)
nên AK$\bot $KH và \[\widehat{AKH}\] = 90°. Trong mặt phẳng (P), K nhìn AH cố định dưới một góc 90° nên quỹ tích của K là đường tròn đường kính AH$\subset $(P).
b) Tính thể tích hình chóp SAHK
Ta có $\frac{{{V}_{SAHK}}}{{{V}_{SAMB}}}=\frac{SA.SH.SK}{SA.SM.SB}=\frac{SK}{SM}.\frac{SH}{SB}$ (3)
$=\frac{SK.SM}{S{{M}^{2}}}.\frac{SH.SB}{S{{B}^{2}}}=\frac{S{{A}^{2}}}{S{{M}^{2}}}.\frac{S{{A}^{2}}}{S{{B}^{2}}}=\frac{{{h}^{4}}}{\left( {{h}^{2}}+2{{R}^{2}} \right)\left( {{h}^{2}}+4{{R}^{2}} \right)}$
$\Rightarrow {{V}_{SAMB}}=\frac{1}{3}.h.\frac{1}{2}.AB.MO=\frac{{{R}^{2}}}{3}h\Rightarrow {{V}_{SHAK}}=\frac{{{R}^{2}}.{{h}^{5}}}{3.\left( {{h}^{2}}+2{{R}^{2}} \right)\left( {{h}^{2}}+4{{R}^{2}} \right)}$
Bài 17. Trong mặt phẳng (P) cho tam giác OAB với OA = OB, AB = 2a và đường cao OH = h . Trên đường thẳng (d) vuông góc với mặt phẳng (P) tại O. Lấy điểm M với OM = x. Gọi E, F lần lượt là hình chiếu vuông gốc của A lên MB và OB, N là giao điểm của đường thẳng EF và (d).
a) Chứng minh rằng MB$\bot $NA và MA$\bot $NB.
b) Tính BE, BF, EF, AF và thể tích tứ diện ABEF theo a, b và x.
c) Tìm vị trí của M trên (d) sao cho tứ diện MNAB có thể tích nhỏ nhất và tính giá trị nhỏ nhất này.
Giải

a) Chứng minh MB$\bot $NA và MA$\bot $NB.
.png)
$\Rightarrow AF\bot mp\left( MOB \right)\Rightarrow AF\bot MB$ (1)
E là hình chiếu của A lên MB nên AE$\bot $MB.
Từ (1) và (2) suy ra: MB$\bot $mp(AEF) $\Rightarrow $ MB$\bot $AN.
Chứng minh tương tự ta cũng có MA$\bot $BN.
b) Tính BE, BF, EF, AF và thể tích ABEF.
* $\Delta $AFB $\backsim $ $\Delta $OHB ($\Delta $ vuông có góc B chung)
$\frac{FB}{HB}=\frac{AB}{OB}\Rightarrow FB=\frac{AB.HB}{OB}=\frac{2{{a}^{2}}}{\sqrt{{{h}^{2}}+{{a}^{2}}}}$
* $\Delta $AEB $\backsim $$\Delta $MHB ($\Delta $ vuông có góc B chung).
$\frac{EB}{MB}=\frac{AB}{MB}\Rightarrow EB=\frac{AB.MB}{MB}=\frac{2{{a}^{2}}}{\sqrt{{{x}^{2}}+{{a}^{2}}+{{h}^{2}}}}$
* $\Delta $AFB$\backsim $ $\Delta $OHB \[\left( \widehat{BOH}\text{ }=\text{ }\widehat{FAB} \right).\]
$\frac{AF}{OH}=\frac{AB}{OB}\Rightarrow AF=\frac{AB.OH}{OB}=\frac{2ah}{\sqrt{{{h}^{2}}+{{a}^{2}}}}$
* $\Delta $BOM$\backsim $ $\Delta $ATE:
$\frac{BO}{AF}=\frac{OM}{FE}\Rightarrow EF=\frac{OM.AF}{BO}$
$EF=\frac{h.\frac{2ah}{\sqrt{{{h}^{2}}+{{a}^{2}}}}}{\sqrt{{{a}^{2}}+{{h}^{2}}}}=\frac{2a{{h}^{2}}}{{{h}^{2}}+{{a}^{2}}}$
Biết AF$\bot $mp(MOB) $\Rightarrow $ AF$\bot $EB.
Theo giả thiết thì AE$\bot $EB. Do đó EB$\bot $mp(AFE) $\Rightarrow $ EB$\bot $FE.
Tam giác FEB là tam giác vuông
Thể tích của tứ diện ABEF là:
\[V=\frac{1}{3}dt\left( \Delta FEB \right).AF=\frac{1}{6}EF.EB.AF=\frac{1}{6}.\frac{2a{{h}^{2}}}{{{h}^{2}}+{{a}^{2}}}.\frac{2{{a}^{2}}}{\sqrt{{{x}^{2}}+{{a}^{2}}+{{h}^{2}}}}.\frac{2ah}{\sqrt{{{h}^{2}}+{{a}^{2}}}}\]
c) Tìm vị trí của M trên d để tứ diện MNAB có thể tích nhỏ nhất.
$\Delta $NOF$\backsim $$\Delta $BOM (vì cùng đồng dạng với $\Delta $BEF) nên:
$\frac{NO}{BO}=\frac{\text{OF}}{OM}\Rightarrow OM.ON=BO.OF$
$\Rightarrow xy=BO.OF$ không đổi.
${{V}_{MNAB}}=\frac{1}{3}\left( x+y \right)dt\left( \Delta OAB \right)$
V nhỏ nhất nếu (x + y) nhỏ nhất.
Theo bất đẳng thức Cô-si: $\frac{x+y}{2}\ge \sqrt{xy}=\sqrt{BO.O\,F}$ không đổi.
Suy ra x + y nhỏ nhất khi x = y =\[\sqrt{BO.OF}\] .
Ta có: $BO=\sqrt{{{h}^{2}}+{{a}^{2}}};$
$O{{F}^{2}}=O{{A}^{2}}-A{{F}^{2}}={{h}^{2}}+{{a}^{2}}-\frac{4{{a}^{2}}{{h}^{2}}}{{{a}^{2}}+{{h}^{2}}}=\frac{{{\left( {{h}^{2}}-{{a}^{2}} \right)}^{2}}}{{{a}^{2}}+{{h}^{2}}}\Rightarrow OF=\frac{\left| {{h}^{2}}-{{a}^{2}} \right|}{\sqrt{{{a}^{2}}+{{h}^{2}}}}$
Vậy $x=y=\sqrt{\left| {{h}^{2}}-{{a}^{2}} \right|}$ .
Bài 18. Cho hai điểm A và B đối xứng với nhau qua mặt phẳng (P), I là giao điểm của AB và mặt phẳng (P). O là một điểm nằm ngoài mặt phẳng (P), có hình chiếu vuông góc xuống mặt phẳng (P) là H, M là điểm chạy trên đường tròn đường kính IH vẽ trong mặt phẳng (P).
a) Chứng minh rằng M là đường vuông góc chung của AB và OM.
b) Chứng minh hai điểm A và B luôn cách đều đường thẳng OM.
c) Cho AB = 2a, MH = x, MI= y. Tính thể tích tứ diện OMAB. Xác định vị trí của M để thể tích có giá trị lớn nhất.
Giải
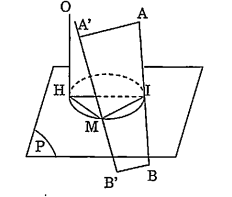
a) Chứng minh IM là đường vuông góc chung của AB và OM.
AB$\bot $(P) $\Rightarrow $ AB$\bot $MI, MI $\subset $ (P) (1)
M ở trên đường tròn đường kính HI nên HM$\bot $MI. (2)
Theo định lý ba đường vuông góc từ (2) suy ra MI$\bot $OM. (3)
Từ (2) và (3) $\Rightarrow $ IM là đường vuông góc chung của AB và OM.
b) Chứng minh A, B cách đều OM.
Chiếu A lên OM thành A', chiếu B lên OM thành B'. Như vậy AA', IM, BB' cùng vuông góc với OM nên chúng cùng song song với một mặt phẳng, do đó ta có:
$\frac{{A}'M}{M{B}'}=\frac{AI}{IB}\Rightarrow M{A}'=M{B}'$
Hai tam giác vuông MA'A và MB'B có MA = MB (do MI là trung trực của AB) và MA' = MB' nên chúng bằng nhau, do đó AA' = BB'.
c) Tính thể tích V của tứ diện OMAB, khi nào V lớn nhất. Ta có:
.png)
Và OH // AB nên OH // mp(AB), do đó khoảng cách từ O đến mặt phẳng (MAB) là HM.
Thể tích V của tứ diện OMAB là:
V = $\frac{1}{3}$ dt($\Delta $MAB).HM = $\frac{1}{3}.\frac{1}{2}$AB.MI.MH =$\frac{1}{6}.2a.y.x\Rightarrow V=\frac{1}{3}a.x.y$
V lớn nhất $\Leftrightarrow $ xy lớn nhất.
Theo bất đẳng thức Cô-si thì: $xy\le \frac{{{x}^{2}}+{{y}^{2}}}{2}=\frac{1}{2}H{{I}^{2}}$
Thể tích V lớn nhất khi đấu “=” xảy ra $\Rightarrow $ x = y, khi M là điểm chính giữa của cung $\overset\frown{HI}$.
Bài 19. Trong mặt phẳng (d) cho đường tròn (T) đường kính AB = 2R. Lấy điểm C di động trên (T). Trên đường thẳng (d) qua A và vuông góc với mặt phẳng (a), lấy điểm E sao cho SA = R. Hạ AH$\bot $SB, AK$\bot $SC.
a) Chứng minh: AK$\bot $mp(SBC), SB$\bot $mp(AHK).
b) Tìm quỹ tích điểm K khi C thay đổi. Tìm giá trị lớn nhất của thể tích tứ diện SAHK.
Giải
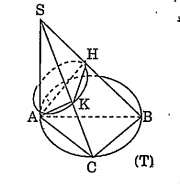
a) Chứng minh AK$\bot $mp(SBC), SB$\bot $mp(AHK),
.png)
$\Rightarrow BC\bot AK$
Giả thiết cho AK$\bot $SC
Suy ra SK$\bot $mp(SBC). Vì AK$\bot $mp(SBC) $\Rightarrow $ AK$\bot $SB.
Giả thiết cho AH$\bot $SB
Suy ra SH$\bot $mp(AK).
b) Tìm quỹ tích của điểm K.
Biết AK$\bot $mp(SBC) $\Rightarrow $ AK$\bot $KH.
Suy ra quỹ tích điểm K khi c thay đổi là đường tròn đường kính nằm trong mặt phẳng (AHK).
Gọi V là thể tích tứ diện SAHK, ta có:
$V=\frac{1}{3}dt\left( \Delta AHK \right).SH=\frac{1}{6}.AK.KH.SH$ (*)
Tính AH: Trong $\Delta $SAB vuông tại A, đường cao AH ta có:
$\frac{1}{A{{H}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{S{{B}^{2}}}=\frac{1}{{{R}^{2}}}+\frac{1}{4{{R}^{2}}}=\frac{5}{4{{R}^{2}}}\Rightarrow AH=\frac{2R\sqrt{5}}{5}$
Trong tam giác vuông SKA ta có:$AK=SA.\sin \beta =R.\sin \beta $ (2)
Trong $\Delta $AKH ta có:
$HK=\sqrt{A{{H}^{2}}-A{{K}^{2}}}=\sqrt{\frac{4{{R}^{2}}}{5}-{{R}^{2}}{{\sin }^{2}}\beta }=R\sqrt{\frac{4}{5}-{{\sin }^{2}}\beta }$ (3)
Thế các giá trị của SH, AK và SH ở (1), (2) và (3) vào (*) ta được:
$V=\frac{1}{6}R\sin \beta .R.\sqrt{\frac{4}{5}-{{\sin }^{2}}\beta }.\frac{R\sqrt{5}}{5}$
$=\frac{{{R}^{3}}\sqrt{5}}{30}\sqrt{{{\sin }^{2}}\beta \left( \frac{4}{5}-{{\sin }^{2}}\beta \right)}\le \frac{{{R}^{3}}\sqrt{5}}{30}.\frac{{{\sin }^{2}}\beta -\frac{4}{5}-{{\sin }^{2}}\beta }{2}=\frac{{{R}^{3}}\sqrt{5}}{75}$
Vậy giá trị lớn nhất của thể tích V của hình chóp SAHK là $\frac{{{R}^{3}}\sqrt{5}}{75}$ , đạt được khi $\sin \beta =\sqrt{\frac{4}{5}}=\frac{2\sqrt{10}}{5}$
