DẠNG 2. MẶT CẦU NGOẠI TIẾP HÌNH CHÓP
A. Phương pháp: Ta có thể sử dụng một trong các cách sau:
1. Chỉ ra được mặt cầu chứa tất cả các đỉnh của hình chóp.
2. Chỉ ra được đáy của hình chóp có đường tròn ngoại tiếp.
3. Tâm của mặt cầu ngoại tiếp hình chóp cách đều tất cả các đỉnh một đoạn bằng R.
4. Tâm mặt cầu ngoại tiếp hình chóp là giao của trục đường tròn ngoại tiếp đáy và mặt phẳng trung trực của một cạnh bên.
B. Bài tập
Bài 1. Cho hình chóp tam giác đều có cạnh đáy bằng a và chiều cao bằng h. Tìm tâm và bán kính của mặt cầu ngoại tiếp hình chóp đó.
Giải
.png)
Gọi hình chóp S.ABC có $\Delta $ABC là tam giác đều cạnh a. Ta có $\Delta $ABC đều kẻ SH$\bot $ (ABC) .
Khi đó SA = SB = SC nên mọi điểm nằm trên SH cách đều A, B, C. Trong mặt phẳng (SAH) đường trung trực của SA cắt SH tại O thì O là tâm mặt cầu ngoại tiếp hình chóp, và bán kính mặt cầu là R = SO.
Gọi I là trung điểm SA thì tứ giác AHIO nội tiếp nên:
$SO.SH=SI.SA\,\,\,\,hay\,\,SO=\frac{S{{A}^{2}}}{2SH}=\frac{S{{A}^{2}}}{2h}$
Mặt khác $S{{A}^{2}}=S{{H}^{2}}+A{{H}^{2}}={{h}^{2}}+{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}=\frac{{{a}^{2}}+3{{h}^{2}}}{3}$
Suy ra $R=SO=\frac{{{a}^{2}}+3{{h}^{2}}}{6h}$
Bài 2. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Chứng minh rằng hình chóp đó có mặt cầu ngoại tiếp. Xác định tâm và tính bán kính mặt cầu đó.
Giải
.png)
Từ giả thiết suy ra tứ giác ABCD là hình thoi. Gọi O là hình chiếu của điểm S xuống đáy.
Vì SA = SB = SC = SD nên OA = OB = OC = OD
Vậy ABCD là hình vuông.
Suy ra S.ABCD có mặt cầu ngoại tiếp.
• Tính bán kính mặt cầu.
Ta có $S{{A}^{2}}+S{{C}^{2}}=A{{C}^{2}}$,suy ra \[\widehat{ASC}=90{}^\circ \] và OS = QA = OC = OB = OD =$\frac{a\sqrt{2}}{2}$
Vậy S(O; R) có tâm O và bán kính R =$\frac{a\sqrt{2}}{2}$
Bài 3. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, mặt bên hợp với mặt đáy một góc p. Xác định tâm và tính bán kính của mặt cầu ngoại tiếp hình chóp.
Giải
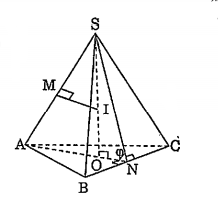
Gọi O là tâm của tam giác đều ABC do S.ABC là hình chóp đều nên SO$\bot $ (ABC).
Vì O cách đều ba điểm A, B, C nên mọi điểm nằm trên đường thẳng SO đều cách đều ba điểm A, B, C.
Trong mặt phẳng (SAO) đường trung trực của SA cắt SO tại I, ta có IA = IS do do IA = IB = IC = IS = R.
Vậy mặt cầu S(I; R) là mặt cầu ngoại tiếp hình chóp SABC.
Gọi M là trung điểm SA, tứ giác AMIO là tứ giác nội tiếp nên ta có SI.SO = SM.SA.
Suy ra R = SI = $\frac{S{{A}^{2}}}{2SO}$
Gọi N là trung điểm của BC ta có ON$\bot $BC và SN$\bot $BC suy ra \[\widehat{SNO}=\varphi \]. Vì$\Delta $ABC là tam giác đều có cạnh bằng a nên AO = $\frac{a\sqrt{3}}{3}$ và ON = $\frac{a\sqrt{3}}{6}$ .
Ta có SO = ON.$\tan \varphi $
$S{{A}^{2}}=S{{O}^{2}}+O{{A}^{2}}=\frac{3{{a}^{2}}}{36}{{\tan }^{2}}\varphi +\frac{3{{a}^{2}}}{9}=\frac{{{a}^{2}}}{12}\left( 4+{{\tan }^{2}}\varphi \right)$
Nên $R=\frac{{{a}^{2}}\left( 4+{{\tan }^{2}}\varphi \right)}{12.2a.\frac{\sqrt{3}}{6}\tan \varphi }$ . Vậy $R=\frac{\sqrt{3}a\left( 4+{{\tan }^{2}}\varphi \right)}{12\tan \varphi }$
Bài 4. Cho hình chóp S.ABC có các cạnh AB = AC = SA = SB = a và hai mặt (SBC) và (ABC) vuông góc với nhau.
a) Chứng minh rằng tam giác SBC vuông.
b) Xác định tâm và bán kính hình cầu ngoại tiếp hình chóp khi SC =x.
Giải
.png)
a) Kẻ AI$\bot $BC. Do AB = AC nên I là trung điểm BC. Khi đó .png)
Từ đó suy ra hai tam giác vuông bằng nhau: $\Delta $ABI = $\Delta $ASI $\Rightarrow $ BI = SI. Mặt khác BI = CI suy ra trung tuyến SI của $\Delta $SBC bằng nửa cạnh đối diện, do đó \[\widehat{BSC}\]= 90°. Vậy $\Delta $SBC vuông tại S.
b) Do tam giác ABC vuông tại S nên I là tâm đường tròn ngoại tiếp của nó.
Gọi O là tâm hình cầu ngoại tiếp bình chóp. Do O cách đều B, E, C nên nằm trên đường thẳng vuông góc với mp (SBC) tại I.
Theo giả thiết (ABC)$\bot $ (SBC) nên đường thẳng OI nằm trong mặt phẳng (ABC).
.png)
Bán kính R của hình cầu ngoại tiếp hình chóp S.ABC cũng là bán kính của đường tròn ngoại tiếp $\Delta $ABC.
Ta tính bán kính R này. Gọi K là giao điểm của đường tròn với AI. Khi đó:
$A{{B}^{2}}=AI.AK=AI.\left( 2R \right)\Rightarrow R=\frac{A{{B}^{2}}}{2AI}=\frac{{{a}^{2}}}{2AI}$
Ta có : $A{{I}^{2}}=A{{C}^{2}}-I{{C}^{2}}={{a}^{2}}-\frac{B{{C}^{2}}}{4}={{a}^{2}}-\frac{{{a}^{2}}+{{x}^{2}}}{4}=\frac{3{{a}^{2}}-{{x}^{2}}}{4}$
Bởi vậy .png)
