DẠNG 2. TÌM TỈ SỐ THỂ TÍCH CỦA HAI KHỐI ĐA DIỆN
A. Phương pháp:
a) Tính thể tích của từng khối đa diện.
b) Sử dụng công thức
$\frac{{{V}_{S.{A}'{B}'{C}'}}}{{{V}_{S.ABC}}}=\frac{S{A}'}{SA}.\frac{S{B}'}{SB}.\frac{S{C}'}{SC}$
B. Bài tập:
Bài 1: Khối chóp S.ABCD có đáy là hình bình hành, M là trung điểm cạnh SC. Mặt phẳng (P) đi qua AM, song song với BD, chia khối chóp thành hai phần. Tính tỉ số thể tích của hai phần đó.
Giải
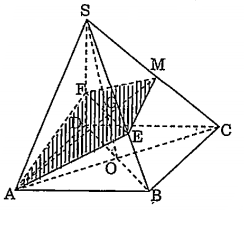
Gọi O là giao điểm 2 đường chéo của hình bình hành ABCD.
AM cắt SO tại G $\Rightarrow $ G là trọng tâm của tam giác SAC $\Rightarrow \frac{SG}{SO}=\frac{2}{3}$
Mặt khác: mp(P) // BD nên sẽ cắt mp(SBD) theo giao tuyến EF qua G và song song với BD \[\left( E\text{ }\in SB,\text{ }F\text{ }\in SD \right)\]
Vì vậy : $\frac{SE}{SB}=\frac{SF}{SD}=\frac{SG}{SO}=\frac{2}{3}$
Vì EF // BD và OB = OD nên GF = GE $\Rightarrow $ \[{{S}_{AFM}}={{S}_{AEM}}\]
Vậy $\frac{{{V}_{SAEMF}}}{{{V}_{SABCD}}}=\frac{\frac{1}{2}{{V}_{SAEMF}}}{\frac{1}{2}{{V}_{SABCD}}}=\frac{{{V}_{SAEM}}}{{{V}_{SABC}}}=\frac{SA}{SA}.\frac{SE}{SB}.\frac{SM}{SC}=\frac{2}{3}.\frac{1}{2}=\frac{1}{3}\Rightarrow \frac{{{V}_{SAEMF}}}{{{V}_{AEMFDCB}}}=\frac{1}{2}$
Bài 2: Cho hình hộp chữ nhật ABCD.ABCD có AB = a, BC = b, AA' = c. Gọi M, N theo thứ tự là trung điểm của A'B' và\[{B}'{C}'\] . Tính tỉ số giữa thể tích khối chóp \[{D}'.DMN\] và thể tích khối hộp chữ nhật\[ABCD.{A}'{B}'{C}'{D}'\].
Giải
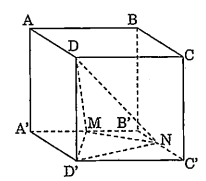
Ta có: \[{{V}_{{D}'.DMN}}\text{ }=\text{ }{{V}_{D.{D}'MN}}\]
Lại có: ${{S}_{{D}'MN}}={{S}_{{A}'{B}'{C}'{D}'}}-\left( {{S}_{{D}'AM}}+{{S}_{{D}'{C}'N}}+{{S}_{{B}'MN}} \right)$
$ab-\left( \frac{ab}{4}+\frac{ab}{8}+\frac{ab}{4} \right)=\frac{3ab}{8}$
Mà ${{V}_{ABCD.{A}'{B}'{C}'{D}'}}=abc$.
Vậy $\frac{{{V}_{{D}'DMN}}}{{{V}_{ABCD.{A}'{B}'{C}'{D}'}}}=\frac{1}{8}$
Bài 3: Cho hình chóp tứ giác đều S.ABCD. Mặt phẳng (P) qua A và vuông góc với BC cắt SB, SC, SD lần lượt tại\[{B}',{C}',{D}'\] . Biết rằng AB = a, $\frac{S{B}'}{SB}=\frac{2}{3}$
a) Tính tỉ số thể tích của hai khối chóp \[S.{A}'{B}'{C}'{D}'\] và S.ABCD.
b) Tính thể tích của khối chóp \[S.{A}'{B}'{C}'{D}'\].
Giải
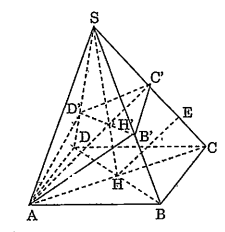
a) Gọi SH là đường cao của hình chóp tứ giác đều S.ABCD; SH cắt (P) tại H';
H là giao điểm của AC và BD.
Vì \[BD\bot \left( SAC \right)\] nên \[BD\bot SC\Rightarrow BD\]// (P).
Từ đó suy ra (P) cắt (SDB) theo giao tuyến \[{B}'{D}'\]// BD.
Do đó $\frac{S{D}'}{SD}=\frac{S{H}'}{SH}=\frac{{B}'{D}'}{BD}=\frac{2}{3}$
${H}'{B}'=H{D}'$ và ${D}'{E}'\bot A{C}'$
Giả sử đường thẳng qua H song song với \[A{C}'\] cắt SC tại E.
Khi đó $E{C}'=EC,\,\,\frac{S{C}'}{SE}=\frac{2}{3}\Rightarrow \frac{SE-S{C}'}{SE}=\frac{1}{3}=\frac{EC}{SE}$
Do đó: \[SC'=2.E{C}'=C{C}'\] .
Ta có $\frac{{{V}_{SAB{D}'}}}{{{V}_{SABD}}}=\frac{2}{3}.\frac{2}{3}=\frac{4}{9}$ (1)
$\frac{{{V}_{S{B}'{C}'{D}'}}}{{{V}_{SBCD}}}=\frac{2}{3}.\frac{2}{3}.\frac{1}{2}=\frac{2}{9}$ (2)
Từ (1), (2) suy ra: ${{V}_{S.A{B}'{C}'{D}'}}={{V}_{S.A{B}'{D}'}}+{{V}_{S.{B}'{C}'{D}'}}=\left( \frac{4}{9}+\frac{2}{9} \right).\frac{{{V}_{S.ABCD}}}{2}=\frac{1}{3}{{V}_{S.ABCD}}$
Vậy \[\frac{{{V}_{S.AB{C}'{D}'}}}{{{V}_{S.ABCD}}}=\frac{1}{3}\]
b) Theo chứng minh trên ta có \[A{C}'\] vừa là đường cao, vừa là trung tuyến của \[\Delta SAC\] nên AS = AC \[\Rightarrow \Delta SAC\] đều. Từ đó suy ra:
$SH=\frac{\sqrt{3}}{2}AC=\frac{\sqrt{3}}{2}.a\sqrt{2}=\frac{\sqrt{6}}{2}a$
\[{{V}_{S.ABCD}}=\frac{1}{3}.\frac{\sqrt{6}}{2}{{a}^{3}}=\frac{\sqrt{6}}{6}{{a}^{3}}\]
Từ đó suy ra: ${{V}_{S.A{B}'{C}'{D}'}}=\frac{\sqrt{16}}{8}{{a}^{3}}$ (đvt).
Bài 4: Cho hình chóp tứ giác đều S.ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh AD, AB, SC. So sánh thể tích của hai khối đa diện do mặt phẳng (MNP) chia ra trên khối chóp.
Giải
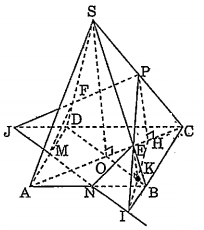
Xét khối đa diện có các định là M, N, E, P, F, B, C, D.
Gọi ${{V}_{1}}$ là thể tích của khối đa diện này.
Ta có: ${{V}_{PIJC}}=\frac{1}{3}{{S}_{CIJ}}.PH$ trong đó PH là khoảng cách từ P đến (ABCD), H $\in $ AC.
AB = a, SO = h.
Ta có: \[{{S}_{CIJ}}={{a}^{2}}+\frac{{{a}^{2}}}{8}=\frac{9{{a}^{2}}}{8}\]
$PH=\frac{1}{2}.SO=\frac{h}{2}$
Do đó: ${{V}_{PIJC}}=\frac{1}{3}.\frac{9{{a}^{2}}}{8}.\frac{h}{2}=\frac{3{{a}^{2}}h}{16}$
Dựng PQ // BC. Ta có : $PQ=\frac{1}{2}BC=BI$
.png)
\[\Rightarrow EP=EI\Rightarrow EK=\frac{1}{2}\text{P}H=\frac{h}{4}\] (EK là khoảng cách từ E đến mp(ABCD))
 .
.
${{V}_{IBNE}}=\frac{1}{3}{{S}_{IBN}}.EK=\frac{1}{3}.\frac{{{a}^{2}}}{8}.\frac{h}{4}=\frac{{{a}^{2}}h}{96}$
Tương tự: ${{V}_{JMDF}}=\frac{{{a}^{2}}h}{96}$
Vậy ${{V}_{1}}=\frac{3{{a}^{2}}h}{16}-2.\frac{{{a}^{2}}h}{96}=\frac{8{{a}^{2}}h}{48}=\frac{{{a}^{2}}h}{6}$
${{V}_{S.ABCD}}=\frac{{{a}^{2}}h}{6}$
$\Rightarrow $ thể tích của khối đa diện còn lại là: ${{V}_{2}}=V-{{V}_{1}}=\frac{{{a}^{2}}h}{3}-\frac{{{a}^{2}}h}{6}=\frac{{{a}^{2}}h}{6}$
Vậy ${{V}_{1}}={{V}_{2}}$
