III. BÀI TẬP TỰ LUYỆN
Bài 1: Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh bằng a. Các cạnh bên tạo với đáy một góc 60°. Hãy tính thể tích của khối chóp đó.
Bài 2: Cho hình lập phương \[ABCD.{A}'{B}'{C}'{D}'\] cạnh a. Gọi K là trung điểm của cạnh BC và I là tâm của mặt bên \[C{C}'{D}'D\] .
a) Hãy xác định thiết diện của hình lập phương với mặt phẳng (AKI).
b) Tính thể tích của các hình đa diện do mặt phẳng (AKT) chia ra trên hình lập phương.
Bài 3: Cho hình hộp chữ nhật \[ABCD.{A}'{B}'{C}'{D}'\]có AB = a, BC = 2a, AA' = a. Lấy điểm M trên cạnh AD sao cho AM = 3MD.
a) Tính thể tích khối chóp \[M.A{B}'C\] .
b) Tính khoảng cách từ M đến mặt phẳng \[\left( A{B}'C \right).\]
Bài 4: Cho hình hộp chữ nhật \[ABCD.{A}'{B}'{C}'{D}'\]có AB = a, BC = b, AA' = c. Gọi E và F lần lượt là những điểm thuộc các cạnh $B{B}'$ và \[D{D}'\] sao cho \[BE=\frac{1}{2}E{B}',\text{ }DF=\frac{1}{2}F{D}'\]. Mặt phẳng (AEF) chia khối hộp chữ nhật \[ABCD.{A}'{B}'{C}'{D}'\]thành hai khối đa diện (H) và \[\left( {{H}'} \right).\] Gọi \[\left( {{H}'} \right)\] là khối đa diện chứa đỉnh \[{A}'\] . Hãy tính thể tích của (H).
Bài 5*: Cho hình hộp \[ABCD.{A}'{B}'{C}'{D}'\]. Gọi E và F lần lượt là trung điểm của \[{B}'{C}'\] và \[{C}'{D}'\]. Mặt phẳng (AEF) chia hình hộp đó thành hai hình đa diện (H) và $({H}')$, trong đó (H) là hình đa diện chứa đỉnh \[{A}'\]. Tính tỉ số giữa thể tích khối đa diện (H) và thể tích khối đa diện $({H}')$.
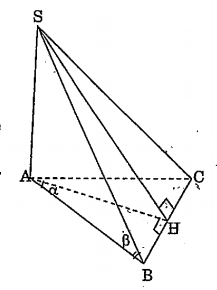
Bài 6*: Cho hình chóp SABC đáy ABC là tam giác cân AB = AC, \[\widehat{BAC}=2\alpha .\] Hai mặt bên SAB, SAC cùng vuông góc với đáy. Cạnh bên SB = m hợp với đáy góc $\beta $ .
a) Gọi H là trung điểm cạnh BC. Chứng minh: $S{{A}^{2}}+A{{H}^{2}}+H{{B}^{2}}=S{{B}^{2}}$ .
b) Tính thể tích của khối chóp.
IV. CÂU HỎI TRẮC NGHIỆM
Câu 1: Cho (H) là khối lăng trụ tam giác đều có tất cả các cạnh bằng a. Thể tích của (H) bằng bao nhiêu?
(A) $\frac{{{a}^{3}}}{2}$
(B) $\frac{{{a}^{3}}\sqrt{2}}{6}$
(C) $\frac{{{a}^{3}}\sqrt{3}}{4}$
(D) $\frac{{{a}^{3}}\sqrt{2}}{3}$
Câu 2: Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a. Thể tích của (H) bằng bao nhiêu?
(A) $\frac{{{a}^{3}}}{3}$
(B) $\frac{{{a}^{3}}\sqrt{2}}{6}$
(C) $\frac{{{a}^{3}}\sqrt{3}}{4}$
(D) $\frac{{{a}^{3}}\sqrt{3}}{2}$
Câu 3: Nếu ba kích thước của khối hộp chữ nhật được tăng thêm k lần thì thể tích của nó tăng lên bao nhiêu lần?
(A) k lần;
(B) ${{k}^{3}}$ lần;
(C) $\frac{k}{3}$ lần;
(D) $\frac{{{k}^{2}}}{3}$ lần.
Câu 4: Cho (H) là khối tứ diện đều cạnh a. Thể tích của (H) bằng bao nhiêu?
(A) $\frac{{{a}^{3}}\sqrt{2}}{6}$
(B) $\frac{{{a}^{3}}\sqrt{3}}{12}$
(C) $\frac{{{a}^{3}}\sqrt{2}}{12}$
(D) $\frac{{{a}^{3}}\sqrt{3}}{4}$
Câu 5: Cho tứ diện ABCD. Gọi \[{B}'\] và \[{C}'\] lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ diện ABCD và khối tứ diện \[{A}'{B}'{C}'{D}'\] bằng bao nhiêu?
(A) $\frac{1}{2}$ ;
(B) $\frac{1}{4}$
(C) $\frac{1}{6}$
(D) $\frac{1}{8}$
Câu 6: Cho hình lăng trụ ngũ giác \[ABCDE.{A}'{B}'{C}'{D}'{E}'\]. Gọi \[{{A}'}',{{B}'}',{{C}'}',{{D}'}',{{E}'}'\] lần lượt là trung điểm của các cạnh\[A{A}',B{B}',C{C}',D{D}',E{E}'\] . Tỷ số thể tích giữa khối lăng trụ \[ABCDE.{{A}'}'{{B}'}'{{C}'}'{{D}'}'{{E}'}'\] và khối lăng trụ \[ABCDE.{A}'{B}'{C}'{D}'{E}'\] bằng bao nhiêu?
(A) $\frac{1}{2}$ ;
(B) $\frac{1}{4}$
(C) $\frac{1}{8}$
(D) $\frac{1}{10}$
Câu 7: Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm \[{A}'\] trên cạnh SA sao cho\[S{A}'=\frac{1}{3}SA\] . Mặt phẳng qua \[{A}'\] và song song với đáy của hình chóp cắt các cạnh SB, SC, SD lần lượt tại \[{B}',{C}',{D}'\]. Khi đó thể tích hình chóp \[S.{A}'{B}'{C}'{D}'\] bằng bao nhiêu?
(A) $\frac{V}{3}$
(B) $\frac{V}{9}$
(C) $\frac{V}{27}$
(D) $\frac{V}{81}$
Câu 8: Cho tứ giác ABCD cố định, S là điểm di động. Thể tích của khối chóp S.ABCD không thay đổi khi:
(A) S di chuyển trên mặt phẳng (α) song song với mặt phẳng (ABCD);
(B) S di chuyển trên đường thẳng a song song với đường thẳng AB;
(C) S di chuyển trên mặt phẳng (P) song song với đường thẳng AB;
(D) S di chuyển bất kì trong không gian.
Câu 9: Cho khối hộp\[ABCD.{A}'{B}'{C}'{D}'\]. Trong các mệnh đề sau mệnh đề nào đúng? Tỷ số thể tích của khối tứ diện ACBD và khối hộp \[ABCD.{A}'{B}'{C}'{D}'\]bằng:
(A) $\frac{1}{2}$ ;
(B) $\frac{1}{3}$
(C) \[\frac{1}{4}\]
(D) $\frac{1}{6}$
Câu 10: Cho hình hộp\[ABCD.{A}'{B}'{C}'{D}'\], gọi O là giao của AC và BD. Trong các mệnh đề sau mệnh đề nào đúng? Tỷ số thể tích của khối chóp \[O.{A}'{B}'{C}'{D}'\] và khối hộp \[ABCD.{A}'{B}'{C}'{D}'\]bằng:
(A) $\frac{1}{2}$
(B) $\frac{1}{3}$
(C) $\frac{1}{4}$
(D) $\frac{1}{6}$
V. ĐÁP SỐ VÀ HƯỚNG DẪN GIẢI
A. Bài tập tự luận:
Bài 1:

Kẻ \[SH\bot \left( ABC \right)\]. \[AH\cap BC=I.\] Có H là trọng tâm của\[\Delta ABC\] .$AI=\frac{\sqrt{3}}{2}=a,\,\,AH=\frac{2}{3}.\frac{\sqrt{3}}{2}a=\frac{\sqrt{3}}{3}a$
$SH=AH.\tan 60{}^\circ =a$
$\Rightarrow {{V}_{S.ABC}}=\frac{1}{3}.\frac{1}{2}.\frac{\sqrt{3}}{2}a.a.a=\frac{\sqrt{3}}{12}{{a}^{3}}$
Bài 2:
.png)
a) Thiết diện của hình lập phương với mặt phẳng (AKT) là tứ giác AKMN.
b) Vì KB = KC nên CF = BA = CF = CD
M là trọng tâm của AFCD $\Rightarrow CM=\frac{1}{3}C{C}'=\frac{a}{3}$
I là trung điểm của \[C{D}'\] nên \[{D}'N=CM=\frac{a}{3}\Rightarrow DN=\frac{2a}{3}\]
${{V}_{1}}$ là thể tích đa diện ADN.KCM (ADN.HCM là khối chóp cụt tam giác có đường cao h = CD). Ta có:${{V}_{1}}=\frac{h}{3}\left( B+{B}'+\sqrt{B{B}'} \right)$
$h=a;\,B={{S}_{ADN}}=\frac{{{a}^{2}}}{3},\,\,{B}'={{S}_{KCM}}=\frac{{{a}^{2}}}{12}$
,${{V}_{1}}=\frac{7{{a}^{3}}}{36},\,{{V}_{2}}$ là thể tích của khối đa diện còn lại.
$\Rightarrow {{V}_{2}}={{a}^{3}}-\frac{7{{a}^{3}}}{36}=\frac{29{{a}^{3}}}{36}$
Bài 3:
.png)
a) ${{V}_{M.ABC}}={{V}_{{B}'.AMC}}$
${{S}_{AMC}}=\frac{3}{4}{{S}_{ADC}}=\frac{3}{4}.\frac{1}{2}.2{{a}^{2}}=\frac{3{{a}^{2}}}{4}$
$\Rightarrow {{V}_{M.A{B}'C}}=\frac{1}{3}.\frac{3{{a}^{2}}}{4}.a=\frac{{{a}^{3}}}{4}$
b)
Gọi h là khoảng cách từ M đến \[\left( A{B}'C \right).\]
${{V}_{M.A{B}'C}}=\frac{1}{3}.{{S}_{A{B}'C}}.h=\frac{{{a}^{3}}}{4}$
$C{{I}^{2}}=C{{A}^{2}}-A{{I}^{2}}=\frac{9{{a}^{2}}}{2}\Rightarrow CI=\frac{3a}{\sqrt{2}}$
${{S}_{A{B}'C}}=\frac{1}{2}.\frac{3a}{\sqrt{2}}.a\sqrt{2}=\frac{3{{a}^{2}}}{2}\Rightarrow h=3.\frac{{{a}^{3}}}{4}:\frac{3{{a}^{2}}}{2}=\frac{a}{2}$
Bài 4:
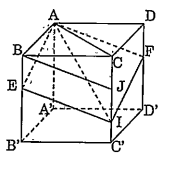
Giả sử (AEF) cắt \[C{C}'\] tại I.
$\Rightarrow $ AEIF là hình bình hành: Trên \[C{C}'\] lấy J sao cho CJ = DF.
Tứ giác CDFJ là hình chữ nhật.
$\Rightarrow $ FJ // AB, FJ = AB.
AF // BJ, AF = BJ.
.png)
$\Rightarrow IJ=EB=DF=JC=\frac{c}{3}$ .Ta có
${{S}_{BCIE}}=\frac{1}{2}\left( \frac{c+2c}{3} \right).b=\frac{bc}{2},\,\,\,{{S}_{DCIF}}=\frac{1}{2}\left( \frac{c+2c}{3} \right).a=\frac{ac}{2}$
$\Rightarrow {{V}_{(H)}}={{V}_{A.BCIE}}+{{V}_{A.DCIF}}=\frac{1}{3}.\frac{bc}{2}a+\frac{1}{3}.\frac{ac}{2}.b=\frac{abc}{3}$
Bài 5:

\[EF\cap {A}'{B}'=I,\,\,\,EF\cap {A}'{D}'=J\]
$AI\cap B{B}'=L,\,\,AJ\cap D{D}'=M$
Gọi \[{{V}_{0}}\] là thể tích khối tứ diện \[A{A}'IJ\]
V là thể tích khối hộp chữ nhật \[ABCD.{A}'{B}'{C}'{D}'\]
Vì \[E{B}'=E{C}'\] và \[{B}'I\] // \[{C}'F\] nên \[IB'=F{C}'=\frac{I{A}'}{3}\] .
Từ đó suy ra hình chóp \[L.{B}'EI\] là ảnh của hình chóp \[A.{A}'IJ\] qua phép vị tự tâm I tỉ số \[k=\frac{1}{3}\]
Do đó \[{{V}_{L{B}'EI}}=\frac{1}{27}{{V}_{0}}\]
Tương tự ${{V}_{MDIF}}=\frac{1}{27}{{V}_{0}}$
Gọi AB = a, BC = b, đường cao hạ từ A xuống (\[{A}'{B}'{C}'{D}'\]) là h thì:
$V={{V}_{ABCD.{A}'{B}'{C}'{D}'}}=h.a.b.\sin \widehat{BAD}$
${{V}_{0}}=\frac{1}{3}.\left( \frac{1}{2}.\frac{3a}{2}.\frac{3b}{2}.\sin \widehat{BAD} \right).h=\frac{3V}{8}$
Vậy ${{V}_{(H)}}={{V}_{0}}-\frac{2}{27}{{V}_{0}}=\frac{25}{27}{{V}_{0}}=\frac{25}{72}V,\,{{V}_{({H}')}}=\frac{47}{72}V$
$\frac{{{V}_{(H)}}}{{{V}_{({H}')}}}=\frac{25}{47}$
Bài 6:
.png)
$\Rightarrow SA$ là đường cao của hình chóp. AB là hình chiếu của SB trên đáy.
Do đó \[\widehat{SBA}=\beta \]
AH là trung tuyến của tam giác cân ABC
$\Rightarrow \widehat{BAH}=\alpha ,\,\,AH\bot BC$
Trong $\Delta $ vuông SAH có: $S{{A}^{2}}+A{{H}^{2}}=S{{H}^{2}}$ (1)
\[~SA\bot \left( ABC \right)\Rightarrow SA\bot BC\] mà \[AH\bot BC\Rightarrow SH\bot BC.\]
Tam giác vuông SHB có: \[S{{H}^{2}}+H{{B}^{2}}=S{{B}^{2}}\] (2)
Thay \[S{{H}^{2}}\] từ (2) vào (1) ta được: $S{{A}^{2}}+A{{H}^{2}}+H{{B}^{2}}=S{{B}^{2}}$ (3) (đpcm)
b) Đặt AH = x, tam giác vuông AHB có: \[HB=x.tan\alpha \]
Tam giác vuông SAB có: \[SA\text{ }=\text{ }m.sin\beta \]
Thay vào (3) ta được: ${{m}^{2}}.{{\sin }^{2}}\beta +{{x}^{2}}.{{\tan }^{2}}\alpha ={{m}^{2}}$
$\Leftrightarrow {{x}^{2}}(1+{{\tan }^{2}}\alpha )={{m}^{2}}.(1-{{\sin }^{2}}\beta )$
$\Leftrightarrow {{x}^{2}}.\frac{1}{{{\cos }^{2}}\alpha }={{m}^{2}}.{{\cos }^{2}}\beta $
Ta có: ${{S}_{ABC}}=\frac{1}{2}BC.AH=BH.AH={{x}^{2}}.\tan \alpha $
Do đó: ${{V}_{SABC}}=\frac{1}{3}{{S}_{ABC}}.SA=\frac{1}{3}{{x}^{2}}.\tan \alpha .m.\sin \beta $ (4)
Thay ${{x}^{2}}={{m}^{2}}.co{{s}^{2}}\alpha .co{{s}^{2}}\beta $ vào ta được:
\[{{V}_{SABC}}=\frac{1}{3}.{{m}^{2}}.co{{s}^{2}}\alpha .co{{s}^{2}}\beta .\tan \alpha .m.\sin \beta \]
$=\frac{1}{3}{{m}^{2}}.cos\alpha .co{{s}^{2}}\beta .\sin \alpha .\sin \beta $
$=\frac{1}{12}.{{m}^{3}}.\sin 2\alpha .\sin 2\beta .cos\beta $
B. Câu hỏi trắc nghiệm
.png)
