DẠNG 3. CHỨNG MINH MỘT SỐ TÍNH CHẤT CỦA CÁC KHỐI ĐA DIỆN ĐỀU. NHẬN DẠNG CÁC KHỐI ĐA DIỆN ĐỀU
A. Phương pháp:
Sử dụng định nghĩa khối đa diện đều.
B. Bài tập
Bài 1: Hai đỉnh của một khối 8 mặt đều cho trước gọi là hai đỉnh đối diện nếu chúng không cùng thuộc một cạnh của khối đó. Đoạn thẳng nối hai đỉnh đối diện gọi là đường chéo của khối 8 mặt đều. Chứng minh rằng trong khối 8 mặt đều:
a) Ba đường chéo cắt nhau tại trung điểm mỗi đường.
b) Ba đường chéo đôi một vuông góc với nhau.
Giải
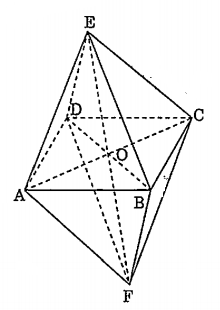
Cho khối 8 mặt đều ABCDEF.
Vì: AE = AF = BE = BF = CE = CF = DE = DF nên A, B, C, D thuộc mặt phẳng trung trực của EF. Do đó ABCD là hình thoi. Từ đó suy ra AC, BD vuông góc với nhau và cắt nhau tại trung điểm O của mỗi đường.
Tương tự AECF cũng là hình thoi nên AC, EF cũng vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường. Từ đó suy ra AC, BD và EF đôi một vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Bài 2: Chứng minh rằng trong hình tám mặt đều, bốn đỉnh cũng nằm trên một mặt phẳng của nó tạo thành một hình vuông.
Giải
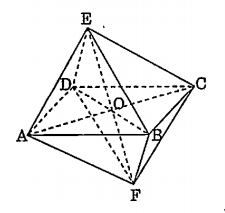
Cho khối tám mặt đều ABCDEF. Vì: AE = AF = BE = BF = CE = CF = DE = DF nên A, B, C, D thuộc mặt phẳng trung trực của EF. Do đó ABCD là hình thoi. Từ đó suy ra AC, BD vuông góc với nhau và cắt nhau tại trung điểm O của mỗi đường. Vì các đường xiên FA, FB bằng nhau nên OA = OB. Do đó AC = BD. Từ đó suy ra hình thoi ABCD là hình vuông.
Bài 3: Chứng minh rằng các trung điểm của các cạnh của một khối tứ diện đều là các đỉnh của một khối tám mặt đều.
Giải
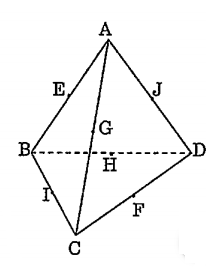
Cho tứ diện đều ABCD, Gọi E, F, I, J, G, H theo thứ tự là trung điểm của các cạnh AB, CD, BC, AD, AC, BD. Lấy trung điểm của một cạnh bất kỳ (ví dụ như lấy điểm E), ta thấy nó cùng với bốn trung điểm của các cạnh không đối diện với nó tạo thành hình chóp tứ giác có các mặt bên là những tam giác đều (hình chóp E.IGJH). Suy ra các trung điểm ấy là các đỉnh của khối đa diện đều loại {3;4} tức là khối tám mặt đều.
