DẠNG 2. BÀI TẬP CHỨNG MINH HAI HÌNH ĐỒNG DẠNG VỚI NHAU
A. Phương pháp:
Để chứng minh hai hình $\mathscr{H}$ và $\mathscr{H}'$ đồng dạng với nhau ta chỉ cần tìm một phép vị tự biến hình $\mathscr{H}$ thành hình $\mathscr{H}_{1}$, sao cho $\mathscr{H}=\mathscr{H}'$
B. Bài tập
Bài 1: Cho một khối tứ diện đều. Hãy chứng minh rằng các trọng tâm của các mặt của nó là các đỉnh của một khối tứ diện đều.
Giải
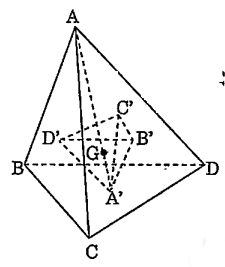
Tứ diện đều ABCD. Gọi \[{A}',{B}',{C}',{D}'\] lần lượt là trọng tâm của các tam giác đều BCD, ACD, ABD, ABC.
Gọi G là trọng tâm tứ diện đều ABCD.
.png)
$\overrightarrow{G{C}'}=-\frac{1}{3}\overrightarrow{GC};\,\,\,\overrightarrow{GD}=-\frac{1}{3}\overrightarrow{GD}$
Do vậy phép vị tự tâm G tỉ số $k=-\frac{1}{3}$ biến khối tứ diện đều ABCD thành khối tứ diện \[{A}'{B}'{C}'{D}'\] hay nói cách khác khối tứ diện ABCD đồng dạng với khối tứ diện \[{A}'{B}'{C}'{D}'\].
Suy ra tứ diện \[{A}'{B}'{C}'{D}'\] đều.
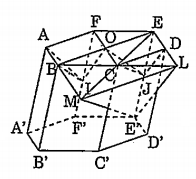
Bài 2: Cho hình lăng trụ \[ABCDEF.{A}'{B}'{C}'{D}'{E}'{F}'\] có đáy là lục giác đều. Gọi O là tâm của lục giác ABCDEF, I là trung điểm của FF, L là giao của các đường thẳng BC và ED. Đường thẳng qua L và song song với AF cắt đường thẳng AB tại M. Chứng minh rằng hai hình chóp I.ABOF và \[{E}'.BMLE\] đồng dạng với nhau.
Giải
Gọi J là trung điểm của\[E{E}'\]. Khi đó: $\overrightarrow{IJ}=\overrightarrow{AO}=\overrightarrow{BC}=\overrightarrow{OD}=\overrightarrow{FE}$
Suy ra hình chóp I.ABOF bằng hình chóp J.ACDE (1)
Mặt khác, ta có O, C, I, D theo thứ tự là trung điểm của EB, EM, EE, EL do đó phép vị tự tâm E tỉ số $\frac{1}{2}$ biến hình chóp \[{E}'.BMLE\] thành hình chóp J.OCDE. (2)
Từ (1), (2) ta có: Hai hình chóp I.ABOF và \[{E}'.BMLE\] đồng dạng với nhau.
Bài 3: Cho hình lập phương\[ABCD.{A}'{B}'{C}'{D}'\]. Gọi E, F, G lần lượt là trung điểm của các cạnh\[{B}'{C}',C{C}',\text{ }{C}'{D}'\]. Chứng minh rằng hai tứ diện \[{C}'EFG\] và \[{B}'{C}'B{A}'\] đồng dạng với nhau.
Giải
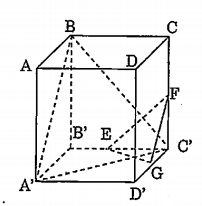
Vì E, F, G lần lượt là trung điểm của \[{B}'{C}',C{C}',\text{ }{C}'{D}'\]nên:
$\overrightarrow{{C}'C}=2.\overrightarrow{{C}'F;}$
$\overrightarrow{{C}'{B}'}=2.\overrightarrow{{C}'E}$
$\overrightarrow{{C}'{D}'}=2.\overrightarrow{{C}'G}$
Suy ra phép vị tự tâm \[{C}'\] tỉ số k = 2 biến tứ diện \[{C}'EFG\] thành tứ diện \[{C}'{B}'C{D}'\] (1)
Mặt khác tứ diện \[{C}'{B}'C{D}'\] bằng tứ diện \[{B}'{C}'B{A}'.\] (2)
Từ (1), (2) suy ra hai tứ diện \[{C}'EFG\] và \[{B}'{C}'B{A}'\]đồng dạng với nhau.
Bài 4: Cho hai hình chóp đều S.ABCD và \[S.{A}'{B}'{C}'{D}'\] . Chứng minh rằng nếu hai góc ASB và \[{A}'{S}'{B}'\] bằng nhau thì hai hình chóp đó đồng dạng.
Giải
S.ABCD và \[S.{A}'{B}'{C}'{D}'\]là các hình chóp đều và \[\widehat{ASB}\text{ }=\text{ }\widehat{{A}'{S}'{B}'}\] . Khi đó hai tam giác cân ASB và A'S'B' đồng dạng. Suy ra:
$\frac{SA}{{S}'{A}'}=\frac{SB}{{S}'{B}'}=\frac{SC}{{S}'{C}'}=\frac{AB}{{A}'{B}'}=\frac{BC}{{B}'{C}'}=\frac{CA}{{C}'{A}'}$
Suy ra hai tứ diện SABC và SA'B'C' có các cạnh tương ứng tỉ lệ. Vậy tứ diện SABC đồng dạng với tứ diện \[{S}'{A}'{B}'{C}'\] .
Gọi f:\[SABC\text{ }\to \text{ }{S}'{A}'{B}'{C}'\]. Vì ABCD và \[{A}'{B}'{C}'{D}'\] là những hình vuông và f biến A, B, C lần lượt thành \[{A}',{B}',{C}'\] nên f biến D thành ${D}'$ .
Vậy f biến hình chóp SABCD thành hình chóp \[S.{A}'{B}'{C}'{D}'\], do đó hai hình chóp đồng dạng.
