DẠNG 3. DÙNG PHƯƠNG PHÁP THỂ TÍCH ĐỂ GIẢI MỘT SỐ BÀI TOÁN HÌNH HỌC
A. Phương pháp:
Dùng hai cách để tính thể tích của cùng một khối đa diện rồi so sánh chúng với nhau để rút ra đại lượng hình học cần tìm.
B. Bài tập:
Bài 1: Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Biết rằng AB = a, BC = b, SA = c. Hãy tính khoảng cách từ A đến mặt phẳng (SBC).
Giải
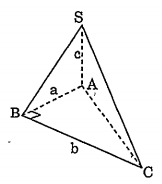
Theo định lý ba đường vuông góc: BC vuông góc với hình chiếu AB của đường xiên SB nên \[BC\bot SB\]. Gọi h là khoảng cách từ A đến mặt phẳng (SBC), V là thể tích hình chóp S.ABC \[V=\frac{1}{6}.SA.AB.BC\text{ }=\frac{1}{6}h.SB.BC\]
$\Rightarrow h=\frac{abc}{b.\sqrt{{{a}^{2}}+{{c}^{2}}}}=\frac{ac}{\sqrt{{{a}^{2}}+{{c}^{2}}}}$
Bài 2: Cho hai đường thẳng chéo nhau d và \[{d}'\]. Trên d lấy hai điểm A và B, trên \[{d}'\]lấy hai điểm C và D sao cho AB = a, CD = c. Biết rằng góc giữa d và \[{d}'\]bằng 60° và khoảng cách giữa d, \[{d}'\]bằng h.
a) Tính thể tích tứ diện ABCD.
b) Giả sử BC vuông góc với CD và BC = b. Tính khoảng cách từ A đến mặt phẳng (BCD).
Giải
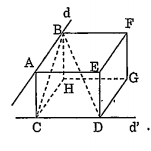
a) Từ các cạnh là AB, CD và AC dựng hình hộp ABFE.CHGD. Khi đó:
${{V}_{ABCD}}=\frac{1}{6}{{V}_{ABFE.CHGD}}=\frac{1}{6}.hac.\sin 60{}^\circ =\frac{hac.\sqrt{3}}{12}$ (1)
b) Gọi \[{h}'\] là khoảng cách từ A đến (BCD).
Ta có: ${{V}_{ABCD}}=\frac{1}{6}.{h}'.bc$ (2) .
Bài 3: Cho khối lăng trụ tam giác \[ABC.{A}'{B}'{C}'\] có đáy là tam giác đều cạnh a, điểm A cách đều ba điểm A, B, C; cạnh bên \[A{A}'\] tạo với mặt phẳng đáy một góc 60°.
a) Tính thể tích của khối lăng trụ đó.
b) Chứng minh rằng mặt bên BCC'B' là một hình chữ nhật.
c) Tính tổng diện tích các mặt bên của hình lăng trụ \[ABC.{A}'{B}'{C}'\] (tổng đó gọi là diện tích xung quanh của hình (hoặc khối) lăng trụ đã cho).
Giải
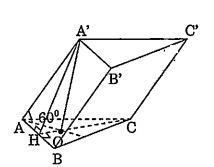
a) Gọi O là tâm của tam giác đều ABC. Vì \[{A}'A={A}'B={A}'C\] nên: \[{A}'O\bot \left( ABC \right).\]
Vậy \[\widehat{{A}'AO}\] = 60°.
Từ đó ta có: \[A{A}'=2.AO=\frac{2\sqrt{3}a}{3}\]
${A}'O=AO.\sqrt{3}=\frac{a\sqrt{3}}{3}.\sqrt{3}=a$
$V=B.h=\frac{{{a}^{2}}\sqrt{3}}{4}.a=\frac{{{a}^{3}}\sqrt{3}}{4}$
b) Vì \[BC\bot AO\] nên \[BC\bot A{A}'\] hay \[BC\bot B{B}'\] .
Tứ giác \[B{B}'{C}'C\] là hình bình hành có 1 góc vuông nên tứ giác \[B{B}'{C}'C\] là hình chữ nhật.
c) \[{{S}_{XQ}}=2.{{S}_{A{A}'{B}'B}}+{{S}_{B{B}'{C}'C}}=2.{A}'H.AB+B{B}'.BC=\frac{{{a}^{2}}\sqrt{3}}{3}\left( \sqrt{13}+2 \right)\]
