DẠNG 2. BÀI TẬP TÌM MẶT PHẲNG ĐỐI XỨNG CỦA MỘT HÌNH VÀ CHỨNG MINH HAI HÌNH BẰNG NHAU
A.Phương pháp
Tìm một phép dời hình biến hình này thành hình kia.
Bài 5. Cho hình lập phương\[ABCD.{A}'{B}'{C}'{D}'\]. Chứng minh rằng
a) Hình chóp \[A.{A}'{B}'{C}'{D}'\] và hình chóp \[C.{A}'{B}'{C}'{D}'\] bằng nhau.
b) Hình lăng trụ \[ABC.{A}'{B}'{C}'\] và \[AD{A}'.BCB'\] bằng nhau.
Giải
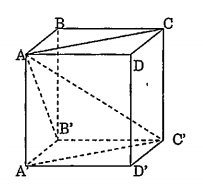
a) Hai tứ diện \[A.{A}'{B}'{C}'\] và \[{C}'.CDA\] bằng nhau (vì có các cạnh bằng nhau) tức là có phép đời hình F biến \[A,{A}',{B}',{C}'\] thành\[{C}',C,D,A\] . Vì F bảo toàn khoảng cách nên F biến \[{D}'\] thành B.
Vậy hai hình chóp \[A.{A}'{B}'{C}'{D}'\]và \[C.{A}'{B}'{C}'{D}'\]bằng nhau.
b) Gọi (P) là mặt phẳng đi qua hai cạnh đối diện AB và \[C{D}'\] thì (P) là mặt phẳng đối xứng của hai lăng trụ \[ABC.{A}'{B}'{C}'\]và \[AD{A}'.BCB'\]. Vậy hai hình lăng trụ đó bằng nhau.
Bài 6. Cho hình lập phương \[ABCD.{A}'{B}'{C}'{D}'\]
a) Tìm phép đối xứng qua mặt phẳng biến \[A,{A}',B,{D}'\] theo thứ tự thành A, D, B, D'.
b) Tìm phép đối xứng qua mặt phẳng biến \[A,{A}',B,{D}'\]theo thứ tự thành \[C,{C}',B,{D}'\]
Giải
a) Phép đối xứng phải tìm biến các điểm không thẳng hàng\[A,\text{ }B,\text{ }{D}'\] thành chính nó nên mặt phẳng đối xứng đó là \[\left( AB{D}' \right).\]
Vậy phép đối xứng phải tìm là phép đối xứng qua \[\left( AB{C}'{D}' \right).\]
b) Phép đối xứng qua\[(BD{D}'{B}')\] .
Bài 7. Chứng minh rằng phép dời hình biến một góc thành một góc bằng nó.
Giải
Trước hết ta có phép dời hình biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự ba điểm đó. Từ đó suy ra phép dời hình f biến góc xOy thành góc \[{x}'O{y}'\]. Lấy A, B khác O theo thứ tự thuộc Ox, Oy thì \[{A}'=f\left( A \right),\text{ }B'=f\left( B \right),\text{ }{A}'\in {O}'{x}',\text{ }B'\in O'y'.\]
Do f bảo tồn khoảng cách nên tam giác AOB bằng tam giác \[{A}'O{B}'\] .
Vậy góc \[xOy\] bằng góc \[{x}'O{y}'\] .
Bài 8. Tìm tất cả các mặt phẳng đối xứng, trục đối xứng, tâm đối xứng của hình hộp chữ nhật.
Giải
Hình hộp chữ nhật có 6 mặt phẳng đối xứng, 3 trục đối xứng và một tâm đối xứng.
