III. BÀI TẬP TỰ LUYỆN
Bài 1: Cho tứ diện ABCD có ba đỉnh B, C, D cố định, còn đỉnh A chạy trên một mặt cầu S (O; r). Tìm quỹ tích trọng tâm G của tứ diện ABCD.
Bài 2: Cho hình chóp tứ giác S.ABCD. Hãy xác định ảnh của hình chóp tứ giác S.ABCD qua phép vị tự tâm S tỉ số $k=\frac{1}{2}$ .
Bài 3: Chứng minh rằng phép vị tự biến một tứ diện thành một tứ diện, biến mặt cầu bán kính r thành mặt cầu bán kính $\left| k \right|.r$ (trong đó k là tỉ số của phép vị tự).
Bài 4: Gọi $(\mathscr{H})$ là hình chóp tứ giác đều có các cạnh đều bằng a.
$\left(\mathscr{H}_{1}\right)$ là hình chóp tứ giác đều có các cạnh đều bằng a1 .
Chứng minh rằng $(\mathscr{H})$ và $\left(\mathscr{H}_{1}\right)$ luôn đồng dạng với nhau.
Bài 5*: Chứng minh: Có năm loại khối đa diện đều. Đó là các khối đa diện đều loại {3;3}, loại {4;3} , loại {3;4} , loại {5;3}, loại {3;5}.
Bài 6*: Chứng minh rằng thực hiện liên tiếp n phép vị tự tâm O sẽ được một phép vị tự tâm O.
IV. CÂU HỎI TRẮC NGHIỆM:
Câu 1: Hình tám mặt đều có bao nhiêu cạnh?
(A) Tám cạnh;
(B) Mười cạnh;
(C) Mười hai cạnh;
(D) Mười sáu cạnh.
Câu 2: Hình mười hai mặt đều có bao nhiêu đỉnh?.
(A) Mười hai đỉnh;
(B) Mười sáu đỉnh;
(C) Hai mươi đỉnh;
(D) Ba mươi đỉnh.
Câu 3: Hình mười hai mặt đều có bao nhiêu cạnh?
(A) Mười hai cạnh;
(B) Mười sáu cạnh;
(C) Hai mươi cạnh;
D) Ba mươi cạnh.
Câu 4: Trong các mệnh đề sau mệnh đề nào sai?
(A) Phép vị tự biến đường thẳng a thành đường thẳng a' song song hoặc trùng với a;
(B) Phép vị tự biến đoạn thẳng thành đoạn thẳng bằng nó;
(C) Phép vị tự biến 1 góc thành 1 góc bằng nó;
(D)Phép vị tự biến một tứ diện thành một tứ diện.
Câu 5: Trong các mệnh đề sau, mệnh đề nào đúng?
Nếu một hình đa điện lồi có số mặt và số đỉnh bằng nhau thì số cạnh của nó:
(A) phải là số lẻ;
(B) phải là số chẵn;
(C) bằng số mặt;
(D) gấp đôi số mặt.
Câu 6: Hình tám mặt đều có bao nhiêu đỉnh?
(A) Sáu đỉnh;
(B) Tám đỉnh;
(C) Mười đỉnh;
(D) Mười hai đỉnh.
Câu 7: Hình hai mươi mặt đều có bao nhiêu đỉnh?
(A) Mười hai đỉnh;
(B) Mười sáu đỉnh;
(C) Hai mười đỉnh;
(D) Ba mươi đỉnh.
Câu 8: Có bao nhiêu phép vị tự biến một tứ diện đều thành chính nó?
(A) Không có;
(B) Một;
(C) Ba;
(D) Vô số
Câu 9: Điền vào chỗ trống trong mệnh đề sau để nó trở thành mệnh đề đúng: “Phép vị tự biến hai đường thẳng song song thành hai đường thẳng...”
(A) Cắt nhau;
B) Chéo nhau;
(C) Song song;
(D) Trùng nhau.
Câu 10: Trong các mệnh đề sau mệnh đề nào sai
(A) Hai tứ diện bằng nhau thì đồng dạng với nhau;
(B) Hai tứ diện bất kì luôn luôn đồng dạng với nhau;
(C) Hai tứ diện đều bất kì luôn luôn đồng dạng với nhau;
(D) Hai tứ diện đều có thể tích bằng nhau thì đồng dạng với nhau.
V. ĐÁP SỐ VÀ HƯỚNG DẪN GIẢI
A. Bài tập tự luận.
Bài 1: Gọi A' là trọng tâm tam giác BCD $\Rightarrow $ A' là điểm cố định.
O là trọng tâm tứ diện ABCD.
Ta có: \[\overrightarrow{{A}'G}\text{ }=\frac{1}{3}\overrightarrow{{A}'A}\] hay${{V}_{\left( A;\frac{1}{3} \right)}}:A\to G$ .
Vì A chạy trên S (O; r) nên quỹ tích của G là ảnh của S (O; r) qua phép vị tự tâm \[{A}'\] , tỉ số k = $\frac{1}{3}$
Bài 2: Ảnh của hình chóp tứ giác S.ABCD qua phép vị tự tâm S tỉ số $k=\frac{1}{2}$ là hình chóp tứ giác S.ABCD.
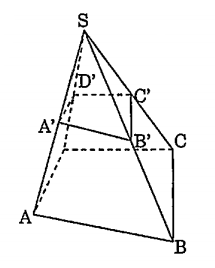
Bài 3: Tứ diện ABCD.
.png)
Ta phải chứng minh \[{A}'{B}'{C}'{D}'\] là tứ diện hay 4 điểm \[{A}',{B}',{C}',{D}'\] không đồng phẳng. Thật vậy, ta có D không nằm trên mp(ABC).
.png)
Suy ra ${D}'$ không nằm trên $mp\left( {A}'{B}'{C}' \right)$ $\Rightarrow $ (đpcm).
Bài 4: Xét phép vị tự tâm O tùy ý và có tỉ số $k=\frac{{{a}_{1}}}{a}$ .
Khi đó, ta thấy hình chóp tứ giác đều có các cạnh đều bằng a là S.ABCD biến thành hình chóp tứ giác đều có các cạnh đều bằng ${{a}_{1}}$, là \[{S}'.{A}'{B}'{C}'{D}'\]. Vậy \[{S}'.{A}'{B}'{C}'{D}'={{S}_{1}}.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\], (với \[{{S}_{1}}.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\] là hình $\mathscr{H}_{1}$).
Bài 5: Gọi d, c và m lần lượt là số đỉnh, số cạnh và số mặt của hình đa diện đều loại {p, q}. Ta có: \[qd=2c=pm.\] Hay:
$\frac{d}{\frac{1}{q}}=\frac{c}{\frac{1}{2}}=\frac{m}{\frac{1}{p}}=\frac{d-c+m}{\frac{1}{q}-\frac{1}{2}+\frac{1}{p}}=\frac{2}{\frac{2p-pq+2q}{2pq}}=\frac{4pq}{2p-pq+2q}$
Từ đó suy ra: \[2p-pq+2q>0\] hay (p - 2)(x - 2) < 4.
Lại có $p\ge 3,\,q\ge 3$ nên chỉ xảy ra các trường hợp:
a) p – 2 = 1, q– 2 = 1 = {p, g} = {3,3}: là khối tứ diện đều.
b) p – 2 = 1, q– 2 = 2 ={p, q}= {3, 4}: là khối tám mặt đều
c) p - 2 = 1, q– 2 = 3 = {p, g} = {3,5}: là khối hai mươi mặt đều.
d) p – 2 = 2, q 2 = 1 = {p, q} = {4,3}: là khối lập phương.
e) p – 2 = 3, q– 2 = 1 = {p, q} ={5,3}: là khối mười hai mặt đều.
Bài 6: Gọi \[{{f}_{1}}\] là phép vị tự tâm O tỉ số ${{k}_{1}}$
${{f}_{2}}$ là phép vị tự tâm O tỉ số ${{k}_{2}}$
\[{{f}_{n}}\] là phép vị tự tâm O tỉ số ${{k}_{n}}$
Lấy điểm M tùy ý, gọi ${{M}_{1}}={{f}_{1}}\left( M \right)\Leftrightarrow \overrightarrow{O{{M}_{1}}}={{k}_{1}}.\overrightarrow{OM}$
${{M}_{2}}={{f}_{2}}\left( {{M}_{1}} \right)\Leftrightarrow \overrightarrow{O{{M}_{2}}}={{k}_{2}}.\overrightarrow{O{{M}_{1}}}$
…
${{M}_{n}}={{f}_{n}}\left( {{M}_{n-1}} \right)\Leftrightarrow \overrightarrow{O{{M}_{n}}}={{k}_{n}}.\overrightarrow{O{{M}_{n-1}}}$
Do đó:$\overrightarrow{O{{M}_{n}}}={{k}_{1}}.{{k}_{2}}...{{k}_{n}}.\overrightarrow{OM}$ .
Từ đó suy ra thực hiện liên tiếp n phép vị tự \[{{f}_{1}},{{f}_{2}},...,{{f}_{n}}\] tâm O sẽ được một phép vị tự tâm O tỉ số \[k={{k}_{1}}.{{k}_{2}}...{{k}_{n}}\]
B. Câu hỏi trắc nghiệm:
.png)
