III. BÀI TẬP TỰ LUYỆN.
Bài 9. Trong không gian \[Oxyz\] cho mặt phẳng (P) có phương trình:
\[2x+y-z-4=0\] và mặt cầu có phương trình ${{(x-3)}^{2}}+{{(y+2)}^{2}}+{{(z-1)}^{2}}=9\,\,\,(S).$
a) Tìm ảnh của mặt phẳng (P) qua mặt phẳng \[Oxy.\]
b) Tìm ảnh của mặt cầu (S) qua mặt phẳng \[Oxy.\]
Bài 10. Cho tứ diện đều ABCD cạnh a. Gọi I và J lần lượt là trung điểm của AB và CD.
a) Chứng minh rằng IJ là đoạn vuông góc chung của AB và CD. Tính IJ.
b) Chứng tỏ rằng tứ diện có ba trục đối xứng.
Bài 11. Cho tứ diện OABC có OA = OB = OC = a, \[\widehat{AOB}=\widehat{AOC}=60{}^\circ ,\] \[\widehat{BOC}=\text{ }90{}^\circ .\]
a) Chứng minh tam giác ABC là tam giác vuông.
b) Gọi I, J lần lượt là trung điểm của OA và BC. Chứng minh rằng mặt phẳng (ODA) là mặt phẳng trung trực của BC và IJ là đoạn vuông góc chung của OA và BC. Tính IJ.
c) Chứng minh tứ diện OABC có hai mặt đối xứng và một trục đối xứng.
Bài 12. Cho mặt phẳng (P) và hai điểm A, B nằm cùng phía đối với (P).
Tìm trên (P) điểm M sao cho tổng các khoảng cách từ đó đến A và B là nhỏ nhất.
Bài 13*. Giả sử phép quay quanh trục d góc α biến mặt phẳng\[\left( P \right)\]chứa d thành mặt phẳng \[\left( {{P}'} \right).\] Chứng minh rằng thực hiện liên tiếp hai phép đối xứng qua hai mặt phẳng \[\left( P \right)\]và \[\left( {{P}'} \right)\] sẽ được phép quay quanh trục d, góc quay $2\alpha $ .
Bài 14*. Cho hai điểm A, B phân biệt và đường thẳng d chéo với đường thẳng AB. Qua điểm M thuộc d dựng hình bình hành \[ABM{M}'\]. Tìm quỹ tích điểm ${M}'$ khi M chạy trên d.
IV. CÂU HỎI TRẮC NGHIỆM.
Câu 1. Gọi f là phép đối xứng qua mặt phẳng (P). Trong các mệnh đề sau, mệnh đề nào sai?
(A) Có một điểm M để f(M) = M;
(B) Có một đường thẳng d để f(d) = 0;
(C) Có một mặt phẳng \[\left( Q \right)\ne \left( P \right)\] sao cho f(Q) = Q;
(D) Có một hình tứ diện (H) sao cho f biến mỗi đỉnh của nó thành chính nó.
Câu 2. Gọi f là phép đối xứng qua tâm O. Trong các mệnh đề sau, mệnh đề nào sai?
(A) Có điểm M để f(M) = M;
(B) Có một đường thẳng d để f(d) = 0;
(C) Có một mặt phẳng (Q) sao cho f(Q) = (Q);
(D) Có tứ diện (H) sao cho f(H) = (H);
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng.
(A) Thực hiện liên tiếp hai phép tịnh tiến sẽ được một phép tịnh tiến;
(B) Thực hiện liên tiếp hai phép đối xứng qua mặt phẳng sẽ được một phép đối xứng qua mặt phẳng
(C) Thực hiện liên tiếp hai phép đối xứng tâm sẽ được một phép đối xứng tâm;
(D) Thực hiện liên tiếp hai phép quay quanh một trục sẽ được một phép quay quanh một trục.
Câu 4. Trong các mệnh đề sau, mệnh đề nào sai?
(A) Phép tịnh tiến biến hai điểm khác nhau thành hai điểm khác nhau;
(B) Phép đối xứng qua mặt phẳng biến hai điểm khác nhau thành hai điểm khác nhau;
(C) Phép quay quanh một trục biến hai điểm khác nhau thành hai điểm khác nhau;
(D) Phép chiếu song song lên một mặt phẳng biến hai điểm khác nhau thành hai điểm khác nhau.
Câu 5. Hình tứ diện đều có bao nhiêu trục đối xứng?
(A) Không có;
B) Ba;
(C) Bốn;
(D) Sáu,
Câu 6. Trong các hình sau đây hình nào có 9 mặt phẳng đối xứng.
(A) Mặt cầu;
B) Tứ diện đều;
(C) Hình lập phương;
(D) Hình bát diện đều.
Câu 7. Trong không gian cho điểm M (-1; 5; 7). Hỏi bốn điểm sau, điểm nào là ảnh của M qua phép đối xứng qua mặt phẳng Oxy.
(A) \[{{M}_{1}}\left( 1;-5;7 \right);\]
(B) \[{{M}_{2}}\left( -1;\text{ }5;-7 \right);\]
(C) \[{{M}_{3}}\left( -1;-5;7 \right);\]
(D) \[{{M}_{4}}\left( 1;-5;-7 \right).\]
Câu 8. Hợp thành của phép tịnh tiến và phép đối xứng tâm là phép nào trong các phép sau đây:
(A) Phép đối xứng trục;
(B) Phép đối xứng tâm;
(C) Phép đồng nhất;
(D) Phép tịnh tiến.
Câu 9. Hợp thành của hai phép đối xứng tâm là các phép nào trong các phép sau đây.
(A) Phép đối xứng trục;
(B) Phép đối xứng tâm;
(C) Phép quay.
(D) Phép tịnh tiến.
Câu 10. Trong các phép sau, phép nào có tính chất biến một đường thẳng a thành đường thẳng ${a}'$ không song song với a:
(A) Phép đối xứng tâm;
(B) Phép tịnh tiến;
(C) Phép đối xứng qua mặt phẳng.
(D) Hợp thành của phép tịnh tiến và phép đối xứng tâm.
V. ĐÁP SỐ VÀ HƯỚNG DẪN GIẢI.
* Bài tập tự luận.
Bài 9.
a) Lấy điểm\[M\left( x,y,z \right)\in d\]. Gọi \[{M}'\left( {x}',{y}',{z}' \right)\] là ảnh của M qua phép đối xứng qua mặt phẳng Oxy. Suy ra \[{M}'\text{ }\in {d}'\] và
.png)
vì x, y, z thỏa mãn phương trình đường thẳng d nên
\[2{x}'+{y}'-\left( -z' \right)-4=0\text{ }\Leftrightarrow 2{x}'+y+z-4=0.\]
Vậy phương trình đường thẳng \[{d}'\] là ảnh của d qua phép đối xứng qua mặt phẳng Oxy là:
\[{d}':\text{ }2x\text{+}y+z4=0\]
b) Phương trình mặt cầu \[\left( {{S}'} \right)\] là ảnh của mặt cầu \[\left( S \right)\] qua phép đối xứng qua mặt phẳng Oxy là:\[\left( {{S}'} \right):\text{ }{{\left( x-3 \right)}^{2}}+{{\left( y+2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=9\]
Bài 10.
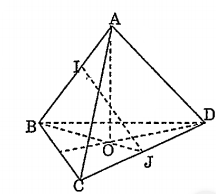
a) \[\Delta JAB\] cân (vì AJ = BJ)
$\Rightarrow $ \[IJ\bot AB\] (1).
\[\Delta ICD\] cân (vì IC = ID)
\[\Rightarrow IJ\bot CD\] (2).
Từ (1) và (2) $\Rightarrow $ IJ là đoạn vuông góc chung của AB và CD.
Ta có \[BJ=\frac{a\sqrt{3}}{2},\text{ }BI=3\] .
Xét \[\Delta IJB\] vuông tại I: \[I{{J}^{2}}=J{{B}^{2}}-B{{I}^{2}}=\frac{3{{a}^{2}}}{4}-\frac{{{a}^{2}}}{4}=\frac{{{a}^{2}}}{2}\]
Vậy $IJ=\frac{a\sqrt{2}}{2}$
b) Tứ diện có ba trục đối xứng đó là trục đi qua các trung điểm của ba cặp cạnh đối diện.
Bài 11.
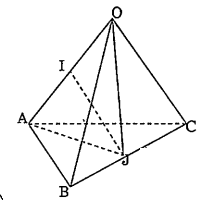
a) Ta có AB = a, AC = a, BC =$a\sqrt{2}$ . Vậy \[\Delta ABC\] vuông tại A.
.png)
Vậy (OJA) là mặt phẳng trung trực của BC.
+\[\Delta JAO\] cân tại J. (do JA = JO)
$\Rightarrow IJ\bot AO\text{ }\left( 1 \right).$
+ \[\Delta IBC\] cân tại I (do IB = IC)
\[\Rightarrow \text{ }IJ\bot BC\,\] (2).
Từ (1) và (2) $\Rightarrow $ IJ là đường vuông góc chung của OA và BC.
Ta có $A{{J}^{2}}={{a}^{2}}+{{\left( \frac{a\sqrt{2}}{2} \right)}^{2}}=\frac{3{{a}^{2}}}{2}\Rightarrow AJ=\frac{a\sqrt{6}}{2}$
Vậy $I{{J}^{2}}=A{{J}^{2}}-A{{I}^{2}}=\frac{3{{a}^{2}}}{2}-\frac{{{a}^{2}}}{4}=\frac{5{{a}^{2}}}{4}\Rightarrow IJ=\frac{a\sqrt{5}}{2}$
c) Tứ diện OABC có một trục đối xứng là đường thẳng IJ và có hai mặt phẳng đối xứng đó là mặt phẳng (OJA) và (IBC).
Bài 12. Gọi \[{A}'\] là điểm đối xứng với A qua mặt phẳng (P). Khi đó:
MA + MB = MA' + MB.
Ta có MA + MB nhỏ nhất khi và chỉ khi \[{A}',M,B\] thẳng hàng, nghĩa là khi M là giao điểm của \[{A}'B\] và (P).
Bài 13.
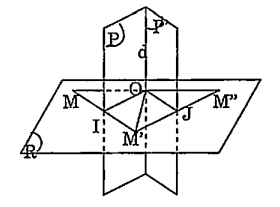
Với mỗi điểm M gọi \[{M}'={{\mathsf{}}_{p}}(M),\,\,{{M}'}'={{\mathsf{}}_{p}}({M}')\].Khi đó \[M,\text{ }{{M}'}'\] thuộc mặt phẳng (R) đi qua M
và vuông góc với d. Giả sử (R) cắt d tại O. Gọi I là hình chiếu vuông góc của M trên (P), J là hình chiếu vuông góc của M trên \[\left( {{P}'} \right).\] Khi đó ta có góc (OI, DJ) = α. Do đó trong mặt phẳng (R):
Góc \[\left( OM,\text{ }O{{M}'}' \right)\] = góc (OM, OM') + góc(OM', OM") = 2α
Từ đó suy ra \[{{M}'}'\] là ảnh của M qua phép quay trục d góc quay 2α.
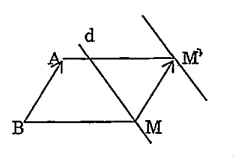
Bài 14. Ta có \[\overrightarrow{M{M}'}=\overrightarrow{BA}\] nên M' là ảnh của M qua phép tịnh tiến theo vectơ \[\overrightarrow{BA}\] . Từ đó suy ra, khi M chạy trên đường thẳng d, quỹ tích điểm M' là đường thẳng \[{d}'\] (là ảnh của d qua phép tịnh tiến theo vectơ \[\overrightarrow{BA}\])
* Câu hỏi trắc nghiệm.
.png)
