II. CÁC DẠNG BÀI TẬP CƠ BẢN VÀ NÂNG CAO
DẠNG 1. BÀI TẬP XÁC ĐỊNH ẢNH CỦA MỘT HÌNH QUA PHÉP VỊ TỰ
A. Phương pháp:
Dùng định nghĩa và tính chất của phép vị tự.
Chú ý: Tìm ảnh của một hình chóp, hình chóp cụt, hình lăng trụ ta chỉ cần tìm ảnh của các đỉnh của chúng.
B. Bài tập:
Bài 1: Chứng minh rằng phép vị tự biến một đường thẳng a thành đường thẳng ${a}'$song song hoặc trùng với a.
Giải
Trên đường thẳng a lấy 3 điểm A, B, C.
Theo tính chất của phép vị tự thì:
\[{{V}_{\left( O;k \right)}}\left( A \right)={A}',\text{ }{{V}_{\left( O;k \right)}}\left( B \right)={B}'\text{ },\text{ }{{V}_{\left( O;k \right)}}\left( C \right)={C}'\] với \[{A}',{B}',{C}'\] thẳng hàng.
Gọi ${a}'$là đường thẳng đi qua \[{A}',{B}',{C}'\]. Ta có:\[{{V}_{\left( O;k \right)}}\left( A \right)={A}'\] .
Ta phải chứng minh $a$ // ${a}'$ hoặc a = ${a}'$. Thật vậy:
.png)
Với \[k\ne 1\] thì AB // A'B' hay a // ${a}'$.
Với k = 1 thì AB $\equiv $ A'B' hay a =${a}'$ .
Bài 2: Cho hình hộp\[ABCD.{A}'{B}'{C}'{D}'\]. Gọi E, F, G lần lượt là trung điểm của các cạnh\[A{A}'\]; AB; AD; O là tâm đối xứng của hình hộp. Hãy tìm ảnh của tứ diện AEFG khi thực hiện liên tiếp hai phép vị tự tâm A tỉ số k = 2 và phép vị tự tâm 0 tỉ số k = – 1.
Giải
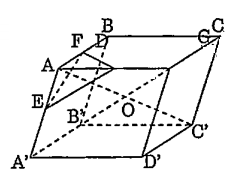
Phép vị tự tâm A tỉ số k = 2 biến A, E, F, G lần lượt thành \[A,\text{ }{A}',\text{ }B,\text{ }D\] .
Phép vị tự tâm O tỉ số k = - 1 biến \[A,\text{ }{A}',\text{ }B,\text{ }D\] lần lượt thành C', C, D', B'.
Vậy ảnh của tứ diện AEFG qua 2 phép vị tự nói trên là tứ diện C'CD'B'.
Bài 3: Cho hai phép vị tự cùng tâm ${{V}_{\left( O;{{k}_{1}} \right)}}$ và \[{{V}_{\left( O;{{k}_{2}} \right)}}\], với ${{k}_{1}}.{{k}_{2}}\ne 1$ . Chứng minh rằng phép biến hình tích: \[F={{V}_{\left( O;{{k}_{2}} \right)}}.{{V}_{\left( O;{{k}_{1}} \right)}}\] cũng là phép vị tự.
Giải
Lấy M là điểm tùy ý, ta có:
\[{{V}_{\left( O;{{k}_{1}} \right)}}:\,\,M\mapsto {M}'\Leftrightarrow \overrightarrow{O{M}'}={{k}_{1}}.\overrightarrow{OM}\] (1)
\[{{V}_{\left( O;{{k}_{2}} \right)}}:M\mapsto {{M}'}'\Leftrightarrow \overrightarrow{O{{M}'}'}={{k}_{2}}.\overrightarrow{O{M}'}\] (2) .
Vậy$F={{V}_{\left( O;{{k}_{2}} \right)}}.{{V}_{\left( O;{{k}_{1}} \right)}}:M\mapsto {{M}'}'$ .
Từ (1) và (2) suy ra: \[\overrightarrow{O{M}'}={{k}_{2}}.{{k}_{1}}.\overrightarrow{OM}\] . (3)
Đẳng thức (3) đúng với mọi điểm M và ${{k}_{1}}.{{k}_{2}}\ne 1$ vậy theo định nghĩa về phép vị tự suy ra: ${{V}_{\left( O;{{k}_{1}}{{k}_{2}} \right)}}:M\mapsto {{M}'}'$
Vậy phép biến hình $F={{V}_{\left( O;{{k}_{2}} \right)}}.{{V}_{\left( O;{{k}_{1}} \right)}}$ , là phép vị tự tâm O, tỉ số ${{k}_{1}}{{k}_{2}}$ .
Bài 4: Cho hai phép vị tự khác tâm ${{V}_{\left( O;{{k}_{1}} \right)}}$ và ${{V}_{\left( O;{{k}_{2}} \right)}}$ với ${{k}_{1}}.{{k}_{2}}\ne 1$ . Chứng minh rằng phép biến hình $F={{V}_{\left( O;{{k}_{1}} \right)}}.{{V}_{\left( O;{{k}_{2}} \right)}}$ cũng là phép vị tự. Gọi O là tâm của phép vị tự này. Chứng minh rằng: O, ${{O}_{1}},\,{{O}_{2}}$ thẳng hàng.
Giải
Xét hai điểm bất kì A, B ta có:
${{V}_{\left( O;{{k}_{1}} \right)}}:\overrightarrow{AB}\mapsto \overrightarrow{{A}'{B}'}\Rightarrow \overrightarrow{{A}'{B}'}={{k}_{1}}.\overrightarrow{AB}$ (1)
${{V}_{\left( O;{{k}_{2}} \right)}}=\overrightarrow{{A}'{B}'}\mapsto \overrightarrow{{{A}'}'{{B}'}'}\Rightarrow \overrightarrow{{{A}'}'{{B}'}'}={{k}_{2}}.\overrightarrow{{A}'{B}'}$ (2)
Vậy $F={{V}_{\left( O;{{k}_{2}} \right)}}.{{V}_{\left( O;{{k}_{1}} \right)}}:\overrightarrow{AB}\mapsto \overrightarrow{{{A}'}'{{B}'}'}$
Từ (1) và (2) suy ra:$\overrightarrow{{{A}'}'{{B}'}'}={{k}_{2}}.{{k}_{1}}\overrightarrow{AB}$ . (3)
Do ${{k}_{1}}.{{k}_{2}}\ne 1$ , (3) đúng với mọi điểm A, B suy ra phép biến hình tích $F={{V}_{\left( O;{{k}_{2}} \right)}}.{{V}_{\left( O;{{k}_{1}} \right)}}$cũng là phép vị tự.
Gọi O là tâm của phép vị tự $F={{V}_{\left( {{O}_{2}};{{k}_{2}} \right)}}.{{V}_{\left( {{O}_{1}};{{k}_{1}} \right)}}$.
Đường thẳng ${{O}_{1}}{{O}_{2}}$ , biến thành chính nó qua phép ${{V}_{\left( {{O}_{1}};{{k}_{1}} \right)}}$ cũng như phép ${{V}_{\left( {{O}_{2}};{{k}_{2}} \right)}}$. Vì vậy đường thẳng ${{O}_{1}}{{O}_{2}}$, biến thành chính nó qua phép vị tự $F={{V}_{\left( {{O}_{2}};{{k}_{2}} \right)}}.{{V}_{\left( {{O}_{1}};{{k}_{1}} \right)}}$.
Giả sử: ${{V}_{\left( {{O}_{1}};{{k}_{1}} \right)}}:O\mapsto {O}'$ hay $\overrightarrow{{{O}_{1}}{O}'}={{k}_{1}}.\overrightarrow{{{O}_{1}}O}$ (4)
và ${{V}_{\left( {{O}_{2}};{{k}_{2}} \right)}}:{O}'\mapsto {{O}'}'$ hay $\overrightarrow{{{O}_{2}}{{O}'}'}={{k}_{2}}.\overrightarrow{{{O}_{2}}{O}'}$ (5)
Do $F={{V}_{\left( {{O}_{2}};{{k}_{2}} \right)}}.{{V}_{\left( {{O}_{1}};{{k}_{1}} \right)}}:O\mapsto {{O}'}'$ nhưng vì O là tâm của phép vị tự $F={{V}_{\left( {{O}_{2}};{{k}_{2}} \right)}}.{{V}_{\left( {{O}_{1}};{{k}_{1}} \right)}}$, nên ${{O}'}'\equiv O$
Vậy (5) có dạng $\overrightarrow{{{O}_{2}}O}={{k}_{2}}.\overrightarrow{{{O}_{2}}{O}'}$ (6)
Do $\overrightarrow{{{O}_{2}}{O}'}=\overrightarrow{{{O}_{2}}{{O}_{1}}}+\overrightarrow{{{O}_{1}}{O}'}$ nên từ (6) suy ra:
$\overrightarrow{{{O}_{2}}O}={{k}_{2}}\left( \overrightarrow{{{O}_{2}}{{O}_{1}}}+\overrightarrow{{{O}_{1}}{O}'} \right)$ (7)
Thay (4) vào (7) có: $\overrightarrow{{{O}_{2}}O}={{k}_{2}}.\left( \overrightarrow{{{O}_{2}}{{O}_{1}}}+{{k}_{1}}\overrightarrow{{{O}_{1}}O} \right)$
hay $\overrightarrow{{{O}_{2}}{{O}_{1}}}+\overrightarrow{{{O}_{1}}O}={{k}_{2}}.\overrightarrow{{{O}_{2}}{{O}_{1}}}+{{k}_{2}}{{k}_{1}}.\overrightarrow{{{O}_{1}}O}$
$\Leftrightarrow \overrightarrow{{{O}_{1}}O}.\left( 1-{{k}_{2}}.{{k}_{1}} \right)=\overrightarrow{{{O}_{1}}{{O}_{2}}}\left( 1-{{k}_{2}} \right)$
Do ${{k}_{1}}.{{k}_{2}}\ne 1$ nên suy ra: $\overrightarrow{{{O}_{1}}O}=\frac{1-{{k}_{2}}}{1-{{k}_{2}}.{{k}_{1}}}.\overrightarrow{{{O}_{1}}{{O}_{2}}}$ (8)
Đẳng thức (8) chứng tỏ $O,\,{{O}_{1}},\,{{O}_{2}}$ thẳng hàng.(đpcm)
