III. BÀI TẬP TỰ LUYỆN
Bài 1: Cho hình hộp ABCD.A’B’C’D’ có đáy là hình thoi ABCD, cạnh a và góc A = 60°. Chân đường vuông góc hạ từ B’ xuống đáy ABCD trùng với giao điểm các đường chéo của đáy. Biết BB = a.
a) Tính góc giữa cạnh bên và đáy.
b) Tính thể tích và diện tích xung quanh hình hộp.
Bài 2: Cho hình chóp S.ABC, đáy ABC là tam giác vuông cân đỉnh A, cạnh AC = a và mặt bên (SBC) vuông với mặt phẳng (ABC). Các mặt bên còn lại hợp với mặt đáy một góc 45°. Tính thể tích hình chóp
Bài 3: Cho khối tám mặt đều ABCDEF cạnh a, có E, F là hai đỉnh không cùng nằm trên một cạnh. Gọi A’, B’, C’, D’, A”, B”, C”, D” lần lượt là trung điểm của các cạnh EA, EB, EC, ED, FA, FB, FC, FD. Chứng minh rằng A’B’C’D’.A”B”C”D” là một hình hộp chữ nhật, tính ba kích thước của nó theo a.
Bài 4: Cho hình chóp S.ABC có đáy ABC là tam giác cân AB = AC, cạnh BC = a, góc A = α. Các cạnh bên SA, SB, SC cùng hợp với đáy gốc p. Tính thể tích khối chóp S.ABC.
Bài 5*: Cho tứ diện gần đều ABCD (AB = CD; AC =BD; AD = BC). Qua mỗi cạnh của tứ diện kẻ mặt phẳng song song với cạnh đối. Các mặt phẳng nhận được xác định một hình hộp.
a) Chứng minh hình hộp nói trên là hình hộp chữ nhật.
b) Chứng minh ${{V}_{ABCD}}=\frac{1}{3}{{V}_{hhcn}}$
c) Gọi IJ, EF, MN là các đường trung bình của tứ diện. Chứng minh: ${{V}_{ABCD}}=\frac{1}{3}IJ.EF.MN$
Bài 6*: Cho hình chóp tứ giác S.ABCD, đáy ABCD có bốn cạnh bằng 1, cạnh bên SC = x. Tính thể tích khối chóp. Định x để thể tích là lớn nhất.
IV. CÂU HỎI TRẮC NGHIỆM:
Câu 1: Khối lập phương thuộc loại nào?
(A) Loại {3 ;4};
(B) Loại {4 ;3};
(C) Loại {3;5};
(D) Loại {5 ;3}.
Câu 2: Tổng diện tích các mặt của một hình lập phương bằng 150m2 . Thể tích của khối lập phương là:
(A) 125m3;
(B) 100m3;
(C) 50m3;
(D) 150m3.
Câu 3: Cho phép vị tự tâm O biến A thành B, biết rằng OB = 3.DA. Khi đó tỉ số phép vị tự là bao nhiêu?
(A) $\frac{1}{3}$
(B) $-\frac{1}{3}$
(C) 3;
(D) $\pm $ 3.
Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng?
Số các cạnh của hình đa diện luôn:
(A) Lớn hơn hoặc bằng 6;
(B) Lớn hơn 6;
(C) Lớn hơn 7;
(D) Lớn hơn hoặc bằng 8.
Câu 5: Trong các mệnh đề sau, mệnh đề nào đúng?
Có hình đa diện lồi mà:
(A) Số đỉnh, số cạnh và số mặt đều lẻ;
(B) Số đỉnh và số cạnh chẵn, còn số các mặt lẻ;
(C) Số đỉnh và số cạnh lẻ, còn số mặt chẵn;
(D) Số đỉnh và số mặt chẵn còn số cạnh lẻ.
Câu 6: Hình lăng trụ tam giác có số đỉnh, số cạnh, số mặt lần lượt tương ứng là:
(A) {6; 9 ;6};
(B) {6; 9;5};
(C) 5; 9;6};
(D) {5; 9:5}.
Câu 7: Có bao nhiêu loại khối đa diện đều?
(A) 3 loại;
(B) 5 loại;
(C) 7 loại;
(D) 10 loại.
Câu 8: Hình chóp tam giác đều có bao nhiêu mặt phẳng đối xứng:
(A) Một;
(B) Hai;
(C) Ba;
(D) Bốn.
Câu 9: Khối 12 mặt đều thuộc loại:
(A) Loại {3;4};
B) Loại {4 ;3};
(C) Loại {3;5};
(D) Loại {5 ;3}.
Câu 10: Hình hộp chữ nhật có bao nhiêu mặt phẳng đối xứng?
(A) Một;
(B) Hai;
(C) Ba;
(D) Bốn.
Câu 11: Ba kích thước của một hình hộp chữ nhật làm thành một cấp số cộng có công sai là 2. Thể tích hình hộp đã cho là 192m3. Khi đó các kích thước của hình hộp là:
(A) 2m, 4m, 6m;
(B) 4m, 6m, 8m;
(C) 6m, 8m, 10m;
(D) 8m, 10m, 12m.
Câu 12: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Biết AB = 5cm, BC = 6cm, SA = 8cm. Thể tích hình chóp S.ABCD là:
(A) 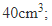
(B) .png)
(C) .png)
(D) .png)
Câu 13: Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh bằng a. Cạnh bên tạo với đáy một góc 60°. Thể tích của khối chóp đó là:
(A) $\frac{\sqrt{3}}{4}{{a}^{3}}$
(B) $\frac{3}{12}{{a}^{3}}$
(C) $\frac{\sqrt{3}}{12}{{a}^{3}}$
(D) $\frac{2}{3}{{a}^{3}}$
Câu 14: Khi tăng đường cao và mỗi cạnh đáy của một hình chóp tứ giác đều lên k lần thì thể tích của hình chóp tăng lên:
(A) .png)
(B) .png)
(C) .png)
(D) .png)
Câu 15: Cho hình chóp tứ giác đều $\mathscr{H}$. Khi đường cao giảm đi n lần, nhưng mỗi cạnh đáy tăng lên 1 lần thì thể tích của $\mathscr{H}$ là:
(A) Không thay đổi;
(B) Tăng lên n lần;
(C) Tăng lên (n-1) lần;
(D) Giảm đi n lần.
Câu 16: Cho khối chóp tam giác có các cạnh đáy bằng 5cm, 6cm, 9cm. Cạnh bên có độ dài 5cm và tạo với đáy một góc 45°. Thể tích của khối chóp là:
(A) $\frac{50\sqrt{2}}{3}c{{m}^{3}}$ ;
(B) $\frac{50}{3}c{{m}^{3}}$
(C) $\frac{50\sqrt{3}}{3}c{{m}^{3}}$
(D)$\frac{25\sqrt{3}}{2}c{{m}^{3}}$ .
Câu 17: Cho lăng trụ đứng ABC.ABC có đáy ABC là tam giác đều cạnh a; đường cao của lăng trụ là h. Khi tăng đường cao lên n lần nhưng mỗi cạnh của tam giác đáy giảm n lần thì thể tích của khối lăng trụ:
(A) Không thay đổi;
(B) Tăng lên n lần;
(C) .png)
(D) Giảm đi n lần.
Câu 18: Điền vào chỗ trống trong mệnh đề sau để nó trở thành mệnh đề đúng:
“Số cạnh của một hình đa diện luôn ... số mặt của hình đa diện ấy”.
(A) bằng;
(B) nhỏ hơn hoặc bằng
(C) nhỏ hơn;
(D) lớn hơn.
Câu 19: Cho tứ diện ABCD. Gọi B’, C’ lần lượt là trung điểm của AB, AC. Khi đó tỉ số thể tích của khối tứ diện ABCD và khối tứ diện AB’C’D bằng bao nhiêu?
(A) $\frac{1}{2}$
(B)$\frac{1}{4}$
(C)$\frac{1}{8}$
(D) $\frac{1}{10}$
Câu 20: Cho hình chóp tứ giác S.ABCD có thể tích bằng v. Lấy điểm A’ trên cạnh SA sao cho SA' = $\frac{1}{2}$SA. Mặt phẳng qua A’ và song song với đáy của hình chóp cắt SB, SC, SD lần lượt tại B’, C’, D’. Khi đó thể tích hình chóp S.AB'CD bằng bao nhiêu?
(A)$\frac{V}{2}$
(B) $\frac{V}{4}$
(C) $\frac{V}{8}$
(D) $\frac{V}{16}$
V. ĐÁP SỐ VÀ HƯỚNG DẪN GIẢI
A. Bài tập tự luyện:
Bài 1:
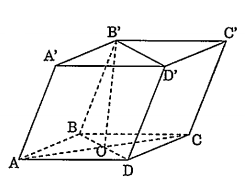
a) Góc giữa cạnh bên BB’ và đáy là góc $\widehat{{B}'BO}$ (vì B’O $\bot $ (ABCD)).
Ta có: \[cos\widehat{{B}'BO}=\frac{OB}{{B}'B}\]
mà OB = a.sin 30°=$\frac{a}{2}$
$\Rightarrow \cos \widehat{{B}'BO}=\frac{1}{2}\Rightarrow \widehat{{B}'BO}=60{}^\circ $
b) ${{S}_{ABCD}}=\frac{{{a}^{3}}\sqrt{3}}{2}$ và ${B}'O=\frac{a\sqrt{3}}{2}\Rightarrow V=\frac{3{{a}^{3}}}{4}$
Các mặt bên có diện tích bằng nhau và bằng : $\frac{{{a}^{2}}\sqrt{3}}{2}$ . Vậy ${{S}_{xq}}=2{{a}^{2}}\sqrt{3}$
Bài 2:
Thể tích của hình chóp SABC là $V=\frac{{{a}^{3}}}{12}$
Bài 3:
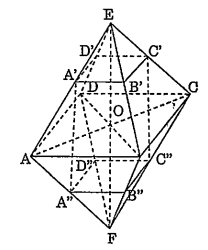
Như ta đã biết ABCD là hình vuông có cạnh bằng a. Do đó A'B'C'D' là hình vuông có cạnh bằng $\frac{a}{2}$ và (A'B'C'D') // (A''B''C''). Ngoài ra ta có: A'A'' // EF nên A'A'' $\bot $ (A''B''C''). Tương tự B'B'', C'C'', D'D'' cũng song song với EF. Từ đó suy ra A'B'C'D'.A''B''C''D'' là một hình hộp chữ nhật. Vì EF = $a\sqrt{2}$ nên A'A" $=\frac{\sqrt{2}}{2}a$
Vậy hình hộp đó có ba kích thước là: $\frac{a}{2},\,\frac{a}{2},\frac{\sqrt{2}}{2}a$
Bài 4:
Gọi O là hình chiếu của S trên đáy ABC.
OA, OB, C là hình chiếu của các cạnh bên SA, SB, SC trên mặt đáy.
Ta có: \[\widehat{SAO}=\widehat{SBO}=\widehat{SCO}=\varphi \].
Các tam giác vuông SAO, SBO, SCO có SO chung các góc A, B, C bằng p nên bằng nhau
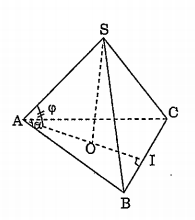
$\Rightarrow $ OA = OB = OC $\Rightarrow $O là tâm đường tròn ngoại tiếp tam giác ABC, O nằm trên đường cao AI của tam giác cân ABC.
Ta có: $\widehat{IAB}=\frac{\alpha }{2};\,BI=\frac{a}{2}$
$AI=BI.\cot \frac{\alpha }{2}=\frac{a}{2}.\cot \frac{\alpha }{2}$
Ta có ${{S}_{ABC}}=\frac{1}{2}BC.AI=\frac{{{a}^{2}}}{4}.\cot \frac{\alpha }{2}$
Ta có $\frac{BC}{\sin A}=2R\Leftrightarrow R=\frac{a}{2.\sin \alpha }$ (R là bán kính đường tròn ngoại tiếp $\Delta $ABC)
Ta được: OA = R$=\frac{a}{2.\sin \alpha }$. Do đó $SO=OA.\tan \varphi =\frac{a.\tan \varphi }{2.\sin \alpha }$
Ta có: ${{V}_{ABC}}=\frac{1}{3}{{S}_{ABC}}.SO=\frac{1}{3}.\frac{{{a}^{2}}}{4}.\cot \frac{\alpha }{2}.\frac{a.\tan \varphi }{2.\sin \alpha }=\frac{{{a}^{3}}.\tan \varphi }{48.{{\sin }^{2}}\frac{\alpha }{2}}$
Bài 5:
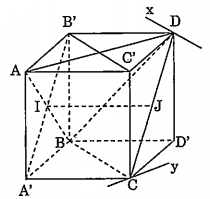
a) Qua D kẻ Dx // BC, qua C kẻ Cy // AD
- AD; Dx xác định mp(P) là mặt phẳng qua AD song song BC.
- BC; Cy xác định mp(Q) là mặt phẳng qua BC song song AD.
Hai góc $\widehat{ADx}$ và $\widehat{BCy}$, có cạnh tương ứng song song nên (P) // (Q). Tương tự đối với cặp mặt phẳng qua AB song song với BC, qua DC song song với AB và với cặp mặt phẳng qua AC song song với BD, qua BD song song với AC.
Sáu mặt phẳng xác định hình hộp A’CD’BAC’DB’. Vì BC = B’C’ mà BC = AD nến B’C’ = AD suy ra tứ giác AC’DB’ là hình chữ nhật. Tương tự các mặt còn lại của hình hộp cũng là các hình chữ nhật. Vì vậy hình hộp nói trên là hình hộp chữ nhật (gọi là hình hộp ngoại tiếp tứ diện gần đều).
b) Ta có: ${{V}_{{A}'ABC}}=\frac{1}{3}{{S}_{{A}'BC}}.A{A}'=\frac{1}{6}{{S}_{{A}'C{D}'B}}.A{A}'=\frac{1}{6}{{V}_{hhcn}}$
Tương tự:${{V}_{C.AC'D}}={{V}_{D.BD'C}}={{V}_{B.AB'D}}=\frac{1}{6}{{V}_{hhcn}}$ .
Vậy ${{V}_{ABCD}}={{V}_{hhcn}}-4.\frac{1}{6}{{V}_{hhcn}}=\frac{1}{3}{{V}_{hhcn}}$ (1)
c) Ta có: đường trung bình IJ của tứ diện ABCD cũng là đường trung bình của hình chữ nhật A’C’D’B’. Do đó IJ = A’C.
Tương tự các đường trung bình EF, MN của tứ diện bằng các cạnh A’B và BB' của hình hộp $\Rightarrow IJ=A'C;EF=A'B;MN=BB'$
Ta có: ${{V}_{hhcn}}=A'C.A'B.BB'=IJ.EF.MN$
Thay vào (1) ta được: ${{V}_{ABCD}}=\frac{1}{3}IJ.EF.MN$
Bài 6: Đáy ABCD có bốn cạnh bằng 1 nên ABCD là một hình thoi, các đường chéo AC và BD vuông góc với nhau và cắt nhau tại trung điểm O của mỗi đường.
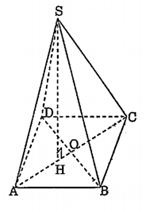
$\Delta $ASC vuông tại S ta có:$AC=\sqrt{{{x}^{2}}+1}$ .
H là hình chiếu của S trên ABCD. SA = SB = SD = 1 $\Rightarrow $ HA = HB = HD.
$\Rightarrow $H là tâm đường tròn ngoại tiếp AABD.
$\Rightarrow $H$\in $ AC.
$\Rightarrow $SH là đường cao của tam giác vuông ASC.
Ta có: SH.AC = SA.SC $\Rightarrow $ $SH=\frac{x}{\sqrt{{{x}^{2}}+1}}$
$O{{B}^{2}}=A{{B}^{2}}-A{{O}^{2}}=\frac{3-{{x}^{2}}}{4}\Rightarrow OB=\frac{1}{2}\sqrt{3-{{x}^{2}}}$ .png)
Ta có: \[{{S}_{ABCD}}=AC.OB=\frac{1}{2}\sqrt{\left( {{x}^{2}}+1 \right)\left( 3-{{x}^{2}} \right)}\]
Vậy \[{{S}_{ABCD}}=\frac{1}{3}{{S}_{ABCD}}.SH=\frac{1}{6}x.\sqrt{3-{{x}^{2}}}\] .png)
${{\left( {{V}_{SABCD}} \right)}^{2}}$ đạt GTLN là $\frac{9}{36.4}$ khi $x=\frac{\sqrt{6}}{2}$
$\Rightarrow \max $ \[{{V}_{SABCD}}=\frac{1}{4}\] khi $x=\frac{\sqrt{6}}{2}$
B. Câu hỏi trắc nghiệm:
.png)
