Bài tập ôn tập chương 1

BÀI TẬP ÔN TẬP CHƯƠNG 1

1. Cho lục giác đều ABCDEF tâm O. Tìm ảnh của tam giác AOF.

a) Qua phép tịnh tiến theo vectơ $\vec{AB}$.

b) Qua phép đối xứng qua đường thẳng BE.

c) Qua phép quay tâm O góc 120°.

BÀI GIẢI

a) Trong phép tịnh tiến theo vectơ $\vec{AB}$ thì: A → B, O → C và F → O.

Vậy $\Delta$AOF → $\Delta$BCO.

b) Trong phép đối xứng qua đường thẳng BE:

A → C, O → O và F → D.

Vậy $\Delta$AOF → $\Delta$COD.

c) Trong phép quay tâm O, góc quay 120° thì:

A → E, O → O và F → D.

Vậy $\Delta$AOF → $\Delta$EOD.

2. Trong mặt phẳng tọa độ Oxy cho điểm A(-1; 2) và đường thẳng d có phương trình 3x + y + 1 = 0. Tìm ảnh của A và d.

a) Qua phép tịnh tiến theo vectơ $\vec{v}$ = (2; 1).

b) Qua phép đối xứng qua trục Oy.

c) Qua phép đối xứng qua gốc tọa độ.

d) Qua phép quay tâm O góc 90°.

BÀI GIẢI

a) A(-1; 2) $\overset{T_{\vec{v}}}{\rightarrow}$ A'(x'; y') ⇒ $\left\{\begin{matrix} x'=-1+2=1\\ y'=2+1=3 \end{matrix}\right.$

- Vậy A'(1; 3).

- Ta thấy A(-1; 2).

Thế vào phương trình: 3x + y + 1 = 0 ⇔ 3.(-1) + 2 + 1 = 0 ⇒ A $\in$ d.

- Vì d qua A nên ảnh của d qua $T_{\vec{v}}$ là d' sao cho

• d' // d ⇒ phương trình d' có dạng 3x + y + c = 0 (c $\neq$ 1).

• d' qua A(1; 3) nên: 3.(1) + 3 + c = 0 ⇔ c = - 6.

- Vậy phương trình của d’ là: 3x + y - 6 = 0.

b) • M(x; y) M' (x'; y') ⇒ $\left\{\begin{matrix} x'=-x\\ y'=y \end{matrix}\right.$ hay $\left\{\begin{matrix} x=-x'\\ y=y' \end{matrix}\right.$

• M(x; y) $\in$ d ⇔ 3x + y + 1 = 0 ⇔ 3.(- x') + y' + 1 = 0

⇔ 3x' - y' - 1 = 0 ⇔ M'(x'; y') $\in$ $d_{1}$: 3x - y - 1 = 0.

c) • A(-1; 2) $A_{2}$(1; -2).

• Ảnh của d qua phép đối xứng tâm Đo là đường thẳng $d_{2}$

• $d_{2}$ // d ⇒ phương trình của $d_{2}$ có dạng 3x + y + c = 0 (c $\neq$ 1).

• $d_{2}$ qua $A_{2}$(1;-2) nên 3.(1) + (-2) + c = 0 ⇔ c = -1.

• Vậy phương trình của $d_{2}$ là 3x + y - 1 = 0.

d)

- Gọi M(-1; 0) và N(0; 2) lần lượt là hình chiếu của A(-1; 2) trên Ox, Oy.

- $Q_{(O,90^{0})}$ biến N thành N'(-2; 0), biến A thành A', biến M thành B(0; -1).

- Vậy $Q_{(O,90^{0})}$ biến hình chữ nhật ONAM thành hình chữ nhật ON'AB.

Do đó A'(-2; -1).

- d qua A và B, $Q_{(O,90^{0})}$ biến A thành A'(-2;-1), biến B thành B'(1; 0).

- Vậy $Q_{(O,90^{0})}$ biến d thành d' qua hai điểm A', B'.

- Do đó phương trình d' là:

$\large \frac{x-x_{A'}}{x_{B'}-x_{A'}}$ = $\large \frac{y-y_{A'}}{y_{B'}-y_{A'}}$ ⇔ $\large \frac{x+2}{1+2}$ = $\large \frac{y+1}{0+1}$ ⇔ x - 3y -1 = 0

3. Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm I(3; -2), bán kính 3.

a) Viết phương trình của đường tròn đó.

b) Viết phương trình ảnh của đường tròn (I; 3) qua phép tịnh tiến theo vectơ $\vec{v}$ = (-2; 1).

c) Viết phương trình ảnh của đường tròn (I; 3) qua phép đối xứng qua trục Ox.

d) Viết phương trình ảnh của đường tròn (I; 3) qua phép đối xứng qua gốc tọa độ.

BÀI GIẢI

a) Phương trình đường tròn tâm I(3; -2), bán kính 3:

$(x-3)^{2}$ + $(y+2)^{2}$ = 9 (C).

b) Gọi M($x_{0}$; $y_{0}$) $\in$ (C).

• M'(x'; y') = $T_{\vec{V}}$(M) ⇔ $\left\{\begin{matrix} x'=x_{0}-2\\ y'=y_{0}+1 \end{matrix}\right.$ ⇔ $\left\{\begin{matrix} x_{0}=x'+2\\ y_{0}=y'-1 \end{matrix}\right.$

• Vì M($x_{0}$; $y_{0}$) $\in$ (C): $(x-3)^{2}$ + $(y+2)^{2}$ = 9 nên

$(x_{0}-3)^{2}$ + $(y_{0}+2)^{2}$ = 9

⇒ $(x'+2-3)^{2}$ + $(y'-1+2)^{2}$ = 9 ⇒ $(x'-1)^{2}$ + $(y'+1)^{2}$ = 9.

• Vậy C' = $T_{\vec{V}}$(C): $(x-1)^{2}$ + $(y+1)^{2}$ = 9.

c) Gọi M($x_{0}$; $y_{0}$) $\in$ (C): $(x-3)^{2}$ + $(y+2)^{2}$ = 9.

• M'(x'; y') = Đ$_{Ox}$(M) ⇔ $\left\{\begin{matrix} x'=x_{0}\\ y'=-y_{0} \end{matrix}\right.$ ⇔ $\left\{\begin{matrix} x_{0}=x'\\ y_{0}=-y' \end{matrix}\right.$

• Vì $(x_{0}-3)^{2}$ + $(y_{0}+2)^{2}$ = 9 nên $(x'-3)^{2}$ + $(-y'+2)^{2}$ = 9

⇒ $(x'-3)^{2}$ + $(y'-2)^{2}$ = 9.

• Vậy (C') = Đ$_{Ox}$ (C): $(x-3)^{2}$ + $(y-2)^{2}$ = 9.

d) Gọi M($x_{0}$; $y_{0}$) $\in$ (C):

$(x-3)^{2}$ + $(y+2)^{2}$ = 9 nên $(x_{0}-3)^{2}$ + $(y_{0}+2)^{2}$ = 9

• M'(x'; y') = Đ$_{O}$(M) ⇔ $\left\{\begin{matrix} x'=-x_{0}\\ y'=-y_{0} \end{matrix}\right.$ ⇔ $\left\{\begin{matrix} x_{0}=-x'\\ y_{0}=-y' \end{matrix}\right.$

• Vì $(x_{0}-3)^{2}$ + $(y_{0}+2)^{2}$ = 9

suy ra $(-x'-3)^{2}$ + $(-y'+2)^{2}$ = 9

⇒ $(x'+3)^{2}$ + $(y'-2)^{2}$ = 9.

• Vậy (C') = Đ$_{O}$ (C): $(x+3)^{2}$ + $(y-2)^{2}$ = 9.

4. Cho vectơ $\vec{v}$, đường thẳng d vuông góc với $\vec{v}$. Gọi d' là ảnh của d qua phép tịnh tiến theo $\large \frac{1}{2}$$\vec{v}$. Chứng minh rằng phép tịnh tiến theo vectơ $\vec{v}$ là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng d và d'.

BÀI GIẢI

- Giả sử qua phép đối xứng trục d, điểm M → $M_{1}$ và gọi H là giao điểm của $MM_{1}$ với d.

- Dễ thấy $\vec{MM_{1}}$ = 2$\vec{HM_{1}}$. (1)

- Qua phép đối xứng trục d', $M_{1}$ → M'.

- Gọi K là giao điểm của $M_{1}$M' với d', ta có: $\vec{M_{1}M'}$ = 2$\vec{M_{1}K}$. (2)

- Năm điểm M, H, K, $M_{1}$, M' thẳng hàng và từ (1), (2) ta có:

$\vec{MM_{1}}$ + $\vec{M_{1}M'}$ = 2. ($\vec{HM_{1}}$ + $\vec{M_{1}K}$) ⇒ $\vec{MM'}$ = 2.$\vec{HK}$ ⇒ $\vec{MM'}$ = $\vec{v}$.

- Vậy M' = $T_{\vec{V}}$ (M).

5. Cho hình chữ nhật ABCD. Gọi O là tâm đối xứng của nó. Gọi I, F, J, E lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tìm ảnh của tam giác AEO qua phép đồng dạng có được từ việc thực hiện liên tiếp phép đối xứng qua đường thẳng IJ và phép vị tự tâm B, tỉ số 2.

BÀI GIẢI

- Ta có: B = Đ$_{IJ}$(A); F = Đ$_{IJ}$(E) và O = Đ$_{IJ}$ (O).

- Do đó: BFO = Đ$_{IJ}$ (AEO).

- Ta có: $\large \frac{BF}{BC}$ = $\large \frac{BO}{BD}$ = $\large \frac{1}{2}$

- Suy ra $\left\{\begin{matrix} \vec{BC}=2\vec{BF}\\ \vec{BD}=2\vec{BO} \end{matrix}\right.$ ⇒ $\left\{\begin{matrix} C=V_{(B,2)}(F)\\ D=V_{(B,2)}(O) \end{matrix}\right.$

Hiển nhiên B = $V_{(B,2)}$ (B).

⇒ Phép vị tự $V_{(B,2)}$ biến tam giác BFO thành tam giác BCD.

- Vậy phép đồng dạng có được từ việc thực hiện liên tiếp phép đối xứng trục Đ$_{IJ}$ và phép vị tự $V_{(B,2)}$, tam giác AEO có ảnh là tam giác BCD.

6. Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm I(1; -3), bán kính 2. Viết phương trình ảnh của đường tròn (I; 2) qua phép đồng dạng có được từ việc thực hiện liên tiếp phép vị tự tâm O, tỉ số 3 và phép đối xứng qua trục Ox.

BÀI GIẢI

• $V_{(O,3)}$ biến I(1; -3) thành J với: $\vec{OJ}$ = 3.$\vec{OI}$

⇒ $\left\{\begin{matrix} x_{J}=3.x_{I}=3\\ y_{J}=3.y_{I}=-9 \end{matrix}\right.$

nên J(3; -9).

• Vậy $V_{(O,3)}$ biến đường tròn (I; 2) thành đường tròn tâm J(3; -9), có bán kính R' = $\mid$3$\mid$R = 6.

• Đ$_{Ox}$ biến I'(3; -9) thành l"(3; 9) nên biến đường tròn (I'; 6) thành đường tròn (I"; 6).

• Vậy phép đồng dạng biến đường tròn (I; 2) thành đường tròn (I''; 6) có phương trình:

$(x-3)^{2}$ + $(y-9)^{2}$ = 36.

7. Cho hai điểm A, B và đường tròn tâm O không có điểm chung với đường thẳng AB. Qua mỗi điểm M chạy trên đường tròn (O) dựng hình bình hành MABN. Chứng minh rằng điểm N thuộc một đường tròn xác định.

BÀI GIẢI

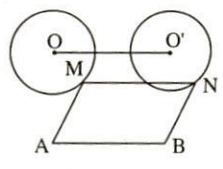
• MABN là hình bình hành ⇒ $\vec{MN}$ = $\vec{AB}$.

• Vậy phép tịnh tiến $T_{\vec{AB}}$ biến M thành N.

• Do đó khi M di động trên (O) thì N di động trên đường tròn (O') là ảnh của (O) qua phép tịnh tiến $T_{\vec{AB}}$.