Chương III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
§1. VECTƠ TRONG KHÔNG GIAN
I. TÓM TẮT LÝ THUYẾT:
1. Định nghĩa và các phép toán về vectơ trong không gian:
* Định nghĩa: Vectơ trong không gian là một đoạn thẳng có hướng. Kí hiệu $\vec{AB}$ chỉ vectơ có điểm đầu A, điểm cuối B. Vectơ còn được kí hiệu là $\vec{a}$, $\vec{b}$, $\vec{x}$, $\vec{y}$,...
• $\vec{AB}$ có giá là đường thẳng AB, có độ dài là đoạn AB.
• Hai vectơ cùng phương có giá song song hoặc trùng nhau.
• Hai vectơ cùng phương thì có thể cùng hướng hay ngược hướng.
• Hai vectơ bằng nhau có cùng độ dài và phải ngược hướng.
• Vectơ $\vec{0}$ = $\vec{AA}$ = $\vec{BB}$ = $\vec{CC}$... có độ dài bằng 0 và phương hướng tùy ý.
2. Phép cộng, phép trừ vectơ:
Có định nghĩa và tính chất giống như phép cộng, phép trừ vectơ trong mặt phẳng.
• Quy tắc ba điểm:
Cộng hai vectơ liên tiếp: $\vec{AB}$ + $\vec{BC}$ = $\vec{AC}$
Trừ hai vectơ cùng gốc: $\vec{AB}$ – $\vec{AC}$ = $\vec{CB}$
• Quy tắc hình bình hành:
Cho hình bình hành ABCD thì: $\vec{AB}$ + $\vec{AD}$ = $\vec{AC}$
.png)
• Quy tắc hình hộp: Cho hình hộp ABCD.A'B'C'D' với ba cạnh có chung đỉnh là AB, AD, AA' và đường chéo cũng chung đỉnh là AC' thì:
$\vec{AB}$ + $\vec{AD}$ + $\vec{AA'}$ = $\vec{AC'}$
.png)
3. Phép nhân vectơ với một số:
* Tích của số thực k với vectơ $\vec{a}$ là vectơ k$\vec{a}$ có:
• k$\vec{a}$ có độ dài là: $\mid$k$\vec{a}$$\mid$ = $\mid$k$\mid$.$\mid$$\vec{a}$$\mid$
• k$\vec{a}$ cùng hướng với $\vec{a}$ nếu k > 0, ngược hướng với $\vec{a}$ nếu k < 0, bằng $\vec{0}$ nếu k = 0.
* Các tính chất của phép nhân cũng giống như trong mặt phẳng.
• Tính chất trung điểm:
I là trung điểm của đoạn AB ⇔ $\vec{MA}$ + $\vec{MB}$ = 2$\vec{MI}$ (với mọi điểm M).
• Tính chất trọng tâm:
G là trọng tâm tam giác ABC ⇔ $\vec{GA}$ + $\vec{GB}$ + $\vec{GC}$ = $\vec{0}$.
4. Sự đồng phẳng của ba vectơ:
a) Định nghĩa:
• Ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ được gọi là đồng phẳng, nếu giá của chúng song song với một mặt phẳng.
• Nói cách khác: Nếu từ một điểm O bất kì, ta vẽ $\vec{OA}$ = $\vec{a}$, $\vec{OB}$ = $\vec{b}$, $\vec{OC}$ = $\vec{c}$ thì bốn điểm O, A, B, C cùng nằm trên một mặt phẳng.
b) Điều kiện để ba vectơ đồng phẳng:
Định lí: Trong không gian cho hai vectơ $\vec{a}$, $\vec{b}$ không cùng phương và vectơ $\vec{c}$. Khi đó $\vec{a}$, $\vec{b}$, $\vec{c}$ đồng phẳng khi và chỉ khi có cặp số m, n duy nhất sao cho $\vec{c}$ = m$\vec{a}$ + n$\vec{b}$.
.png)
5. Phân tích một vectơ theo ba vectơ không đồng phẳng:
Định lí: Trong không gian cho ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ không đồng phẳng khi đó với mọi vectơ $\vec{x}$ ta đều tìm được một bộ ba số m, n, p duy nhất sao cho $\vec{x}$ = m$\vec{a}$ + n$\vec{b}$ + p$\vec{c}$.
.png)
II. GIẢI ĐÁP CÂU HỎI SÁCH GIÁO KHOA:
1. Cho hình tứ diện ABCD. Hãy chỉ ra các vectơ có điểm đầu là A và điểm cuối là các đỉnh còn lại của hình tứ diện. Các vectơ đó có cùng nằm trong một mặt phẳng không?
BÀI GIẢI
.png)
• Các vectơ có điểm đầu là A và điểm cuối là các đỉnh còn lại của hình tứ diện là: $\vec{AB}$, $\vec{AC}$, $\vec{AD}$.
• Ba vectơ này không nằm trong một mặt phẳng.
2. Cho hình hộp ABCD.A'B'C'D'. Hãy kể tên các vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vectơ $\vec{AB}$.
BÀI GIẢI
• $\vec{AB}$ = $\vec{DC}$ = $\vec{D'C'}$ = $\vec{A'B'}$.
3. Cho hình hộp ABCD.EFGH. Hãy thực hiện các phép toán sau đây (h.dưới).
a) $\vec{AB}$ + $\vec{CD}$ + $\vec{EF}$ + $\vec{HG}$;
b) $\vec{BE}$ - $\vec{CG}$.
.png)
BÀI GIẢI
.png)
4. Trong không gian cho hai vectơ $\vec{a}$ và $\vec{b}$ khác vectơ – không. Hãy dựng vectơ $\vec{m}$ = 2$\vec{a}$, $\vec{n}$ = -3$\vec{b}$ và dựng vectơ $\vec{p}$ = $\vec{m}$ + $\vec{n}$.
BÀI GIẢI
• Với mỗi vectơ $\vec{a}$, ta hãy xác định vectơ $\vec{m}$ = 2$\vec{a}$. Vectơ $\vec{m}$ này cùng hướng với $\vec{a}$ và có độ dài gấp hai lần độ dài của vectơ $\vec{a}$.
• Với vectơ $\vec{b}$, ta hãy xác định vectơ $\vec{n}$ = -3$\vec{b}$. Vectơ này ngược hướng với vectơ $\vec{b}$ và có độ dài gấp ba lần độ dài của vectơ $\vec{b}$.
• Lấy một điểm O bất kì trong không gian, vẽ $\vec{OA}$ = $\vec{m}$ rồi vẽ tiếp $\vec{AB}$ = $\vec{n}$.
Ta có $\vec{OB}$ = $\vec{m}$ + $\vec{n}$ = 2$\vec{a}$ - 3$\vec{b}$.
5. Cho hình hộp ABCD.EFGH. Gọi I và K lần lượt là trung điểm của các cạnh AB và BC. Chứng minh rằng các đường thẳng IK và ED song song với mặt phẳng (AFC). Từ đó suy ra ba vectơ $\vec{AF}$, $\vec{IK}$, $\vec{ED}$ đồng phẳng.
BÀI GIẢI
.png)
• Vì IK // AC $\subset$ (AFC) ⇒ IK // (AFC).
ED // FC $\subset$ (AFC) ⇒ ED // (AFC).
⇒ Các vectơ $\vec{IK}$, $\vec{ED}$ có giá song song với mp(AFC) và riêng vectơ $\vec{AF}$ có giá thuộc mặt phẳng (AFC) nên ba vectơ này đồng phẳng.
6. Cho hai vectơ $\vec{a}$ và $\vec{b}$ đều khác vectơ $\vec{0}$. Hãy dựng vectơ $\vec{c}$ = 2$\vec{a}$ - $\vec{b}$ và giải thích tại sao ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ đồng phẳng.
BÀI GIẢI
• Trước hết ta dựng vectơ 2$\vec{a}$ và vectơ -$\vec{b}$. Theo quy tắc của phép trừ hai vectơ, ta tìm được vectơ $\vec{c}$ = 2$\vec{a}$ - $\vec{b}$ = 2$\vec{a}$ +(-$\vec{b}$) vì $\vec{c}$ = 2$\vec{a}$ - $\vec{b}$ nên ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ đồng phẳng (vì có dạng $\vec{c}$ = m$\vec{a}$ + n$\vec{b}$ trong đó m = 2 và n = -1).
7. Cho ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ trong không gian. Chứng minh rằng nếu:
m$\vec{a}$ + n$\vec{b}$ + p$\vec{c}$ = $\vec{0}$ và một trong ba số m, n, p khác không thì ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ đồng phẳng.
BÀI GIẢI
• Ta có: m$\vec{a}$ + n$\vec{b}$ + p$\vec{c}$ = $\vec{0}$ và giả sử p $\neq$ 0.
• Khi đó ta có thể viết p$\vec{c}$ = - m$\vec{a}$ - n$\vec{b}$ ⇔ $\vec{c}$ = - $\large \frac{m}{p}$$\vec{a}$ - $\large \frac{n}{p}$$\vec{b}$
• Vậy ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ đồng phẳng.
III. GIẢI BÀI TẬP SÁCH GIÁO KHOA:
1. Cho hình lăng trụ tứ giác ABCD. A'B'C'D'. Mặt phẳng (P) cắt các cạnh bên AA', BB', CC', DD' lần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ. Hãy chỉ ra các vectơ:
a) Cùng phương với $\vec{IA}$;
b) Cùng hướng với $\vec{IA}$;
c) Ngược hướng với $\vec{IA}$.
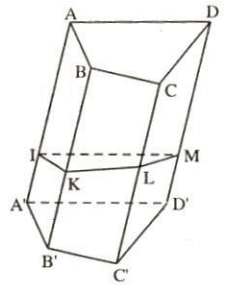
BÀI GIẢI
a) Các vectơ cùng phương với $\vec{IA}$ là:
$\vec{IA'}$, $\vec{KB}$, $\vec{KB'}$, $\vec{LC}$, $\vec{LC'}$, $\vec{MD}$, $\vec{MD'}$.
b) Các vectơ cùng hướng với $\vec{IA}$ là:
$\vec{KB}$, $\vec{LC}$, $\vec{MD'}$
c) Các vectơ ngược hướng với $\vec{IA}$ là:
$\vec{IA'}$, $\vec{KB'}$, $\vec{LC'}$, $\vec{MD'}$.
2. Cho hình hộp ABCD.A'B'C'D. Chứng minh rằng:
a) $\vec{AB}$ + $\vec{B'C'}$ + $\vec{DD'}$ = $\vec{AC'}$;
b) $\vec{BD}$ - $\vec{D'D}$ - $\vec{B'D'}$ = $\vec{BB'}$;
c) $\vec{AC}$ + $\vec{BA'}$ + $\vec{DB}$ + $\vec{C'D}$ = $\vec{0}$.
.png)
BÀI GIẢI
a) Chứng minh: $\vec{AB}$ + $\vec{B'C'}$ + $\vec{DD'}$ = $\vec{AC'}$.
• Đưa về các vectơ cùng gốc A, ta có:
$\vec{AB}$ + $\vec{B'C'}$ + $\vec{DD'}$ = $\vec{AB}$ + $\vec{AD}$ + $\vec{AA'}$ = $\vec{AC'}$. (quy tắc hình hộp)
b) Chứng minh: $\vec{BD}$ - $\vec{D'D}$ - $\vec{B'D'}$ = $\vec{BB'}$
• Ta có: $\vec{BD}$ - $\vec{D'D}$ - $\vec{B'D'}$ = ($\vec{BD}$ + $\vec{DD'}$) + $\vec{D'B'}$ (tính chất vectơ đối)
= $\vec{BD'}$ + $\vec{D'B'}$ = $\vec{BB'}$. (quy tắc ba điểm)
c) Chứng minh: $\vec{AC}$ + $\vec{BA'}$ + $\vec{DB}$ + $\vec{C'D}$ = $\vec{0}$.
• Do các mặt chéo của hình hộp là hình bình hành nên:
$\vec{BA'}$ = $\vec{CD'}$, $\vec{DB}$ = $\vec{D'B'}$, $\vec{C'D}$ = $\vec{B'A}$.
• Do đó: $\vec{AC}$ + $\vec{BA'}$ + $\vec{DB}$ + $\vec{C'D}$
= $\vec{AC}$ + $\vec{CD'}$ + $\vec{D'B'}$ + $\vec{B'A}$ = $\vec{AA}$ = $\vec{0}$ (quy tắc ba điểm)
3. Cho hình bình hành ABCD. Gọi S là một điểm nằm ngoài mặt phẳng hình bình hành. Chứng minh rằng: $\vec{SA}$ + $\vec{SC}$ = $\vec{SB}$ + $\vec{SD}$
BÀI GIẢI
.png)
• Gọi I là tâm của hình bình hành ABCD.
• Áp dụng tính chất trung điểm, ta có:
$\vec{SA}$ + $\vec{SC}$ = $2\vec{SI}$ và $\vec{SB}$ + $\vec{SD}$ = $2\vec{SI}$
• Do đó: $\vec{SA}$ + $\vec{SC}$ = $\vec{SB}$ + $\vec{SD}$
4. Cho hình tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng:
a) $\vec{MN}$ = $\large \frac{1}{2}$($\vec{AD}$ + $\vec{BC}$);
b) $\vec{MN}$ = $\large \frac{1}{2}$($\vec{AC}$ + $\vec{BD}$).
BÀI GIẢI
.png)
a) Chứng minh: $\vec{MN}$ = $\large \frac{1}{2}$($\vec{AD}$ + $\vec{BC}$).
• Ta có: $\vec{MN}$ = $\large \frac{1}{2}$($\vec{MC}$ + $\vec{MD}$) (tính chất trung điểm)
= $\large \frac{1}{2}$($\vec{MB}$ + $\vec{BC}$ + $\vec{MA}$ + $\vec{AD}$)
= $\large \frac{1}{2}$($\vec{BC}$ + $\vec{AD}$) (vì $\vec{MB}$, $\vec{MA}$ đối nhau).
b) Chứng minh: $\vec{MN}$ = $\large \frac{1}{2}$($\vec{AC}$ + $\vec{BD}$).
• Ta có: $\vec{AC}$ = $\vec{AM}$ + $\vec{MN}$ + $\vec{NC}$ (1)
$\vec{BD}$ = $\vec{BM}$ + $\vec{MN}$ + $\vec{ND}$ (2)
.png)
5. Cho hình tứ diện ABCD. Hãy xác định hai điểm E, F sao cho:
a) $\vec{AE}$ = $\vec{AB}$ + $\vec{AC}$ + $\vec{AD}$;
b) $\vec{AF}$ = $\vec{AB}$ + $\vec{AC}$ - $\vec{AD}$.
BÀI GIẢI
.png)
a) Xác định điểm E sao cho: $\vec{AE}$ = $\vec{AB}$ + $\vec{AC}$ + $\vec{AD}$.
• Gọi I là trung điểm của BC, ta có: $\vec{AB}$ + $\vec{AC}$ = 2$\vec{AI}$ = $\vec{AJ}$
(J là đỉnh thứ tư của hình bình hành ABJC)
• Vậy $\vec{AE}$ = $\vec{AB}$ + $\vec{AC}$ + $\vec{AD}$ ⇔ $\vec{AE}$ = $\vec{AJ}$ + $\vec{AD}$.
• Vậy E là đỉnh thứ tư của hình bình hành AJED.
b) Xác định điểm F sao cho: $\vec{AF}$ = $\vec{AB}$ + $\vec{AC}$ - $\vec{AD}$.
• Ta có: $\vec{AB}$ + $\vec{AC}$ = $\vec{AJ}$. (câu a)
• Vậy $\vec{AF}$ = $\vec{AB}$ + $\vec{AC}$ - $\vec{AD}$ ⇔ $\vec{AF}$ = $\vec{AJ}$ – $\vec{AD}$
⇔ $\vec{AJ}$ = $\vec{AF}$ + $\vec{AD}$.
• Vậy F là đỉnh thứ tư của hình bình hành ADJF.
6. Cho hình tứ diện ABCD. Gọi G là trọng tâm tam giác ABC. Chứng minh rằng: $\vec{DA}$ + $\vec{DB}$ + $\vec{DC}$ = 3$\vec{DG}$.
BÀI GIẢI
.png)
• Theo quy tắc ba điểm, ta có:
.png)
⇒ $\vec{DA}$ + $\vec{DB}$ + $\vec{DC}$ = 3$\vec{DG}$ + ($\vec{GA}$ + $\vec{GB}$ + $\vec{GC}$). (1)
• Mà G là trọng tâm của tam giác ABC nên:
$\vec{GA}$ + $\vec{GB}$ + $\vec{GC}$ = $\vec{0}$. (2)
• (1) và (2) ⇒ $\vec{DA}$ + $\vec{DB}$ + $\vec{DC}$ = 3$\vec{DG}$. (đpcm)
7. Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh rằng:
a) $\vec{IA}$ + $\vec{IB}$ + $\vec{IC}$ + $\vec{ID}$ = $\vec{0}$;
b) $\vec{PI}$ = $\large \frac{1}{4}$($\vec{PA}$ + $\vec{PB}$ + $\vec{PC}$ + $\vec{PD}$).
BÀI GIẢI
.png)
a) Chứng minh: $\vec{IA}$ + $\vec{IB}$ + $\vec{IC}$ + $\vec{ID}$ = $\vec{0}$.
• Ta có: $\vec{IA}$ + $\vec{IB}$ + $\vec{IC}$ + $\vec{ID}$ = $\vec{IA}$ + $\vec{IC}$ + $\vec{IB}$ + $\vec{ID}$
= 2$\vec{IM}$ + 2$\vec{IN}$ (tính chất trung điểm)
= 2($\vec{IM}$ + $\vec{IN}$) = $\vec{0}$ (vì I là trung điểm MN)
b) Chứng minh $\vec{PI}$ = $\large \frac{1}{4}$($\vec{PA}$ + $\vec{PB}$ + $\vec{PC}$ + $\vec{PD}$).
• Ta có: $\vec{PA}$ + $\vec{PB}$ + $\vec{PC}$ + $\vec{PD}$ = 4$\vec{PI}$ + ($\vec{IA}$ + $\vec{IB}$ + $\vec{IC}$ + $\vec{ID}$) = 4$\vec{PI}$
⇒ $\vec{PI}$ = $\large \frac{1}{4}$($\vec{PA}$ + $\vec{PB}$ + $\vec{PC}$ + $\vec{PD}$). (đpcm)
8. Cho hình lăng trụ tam giác ABC.A'B'C' có $\vec{AA'}$ = $\vec{a}$, $\vec{AB}$ = $\vec{b}$, $\vec{AC}$ = $\vec{c}$. Hãy phân tích (hay biểu thị) các vectơ $\vec{B'C}$, $\vec{BC'}$ qua các vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$.
BÀI GIẢI
.png)
Theo quy tắc hiệu hai vectơ và quy tắc hình bình hành, ta có:
• $\vec{B'C}$ = $\vec{AC}$ - $\vec{AB'}$ = $\vec{AC}$ - ($\vec{AB}$ + $\vec{AA'}$) vì AA'B'B là hình bình hành.
Vậy $\vec{B'C}$ = $\vec{c}$ - $\vec{a}$ - $\vec{b}$.
• $\vec{BC'}$ = $\vec{AC'}$ – $\vec{AB}$ =($\vec{AA'}$ + $\vec{AC}$) – $\vec{AB}$ vì AA'C'C là hình bình hành.
Vậy $\vec{BC'}$ = $\vec{a}$ + $\vec{c}$ - $\vec{b}$.
9. Cho tam giác ABC. Lấy điểm S nằm ngoài mặt phẳng (ABC). Trên đoạn SA lấy điểm M sao cho $\vec{MS}$ = -2$\vec{MA}$ và trên đoạn BC lấy điểm N sao cho $\vec{NB}$ = - $\large \frac{1}{2}$$\vec{NC}$. Chứng minh rằng ba vectơ $\vec{AB}$, $\vec{MN}$, $\vec{SC}$ đồng phẳng.
BÀI GIẢI
.png)
• Ta có: $\vec{MN}$ = $\vec{MS}$ + $\vec{SC}$ + $\vec{CN}$ (1)
Và: $\vec{MN}$ = $\vec{MA}$ + $\vec{AB}$ + $\vec{BN}$.
⇒ 2$\vec{MN}$ = 2$\vec{MA}$ + 2$\vec{AB}$ + 2$\vec{BN}$ (2)
• Lấy (1) + (2) ta được:
.png)
• Vậy $\vec{AB}$, $\vec{MN}$, $\vec{SC}$ đồng phẳng.
10.Cho hình hộp ABCD.EFGH. Gọi K là giao điểm của AH và DE, I là giao điểm của BH và DF. Chứng minh ba vectơ $\vec{AC}$, $\vec{KI}$, $\vec{FG}$ đồng phẳng.
BÀI GIẢI
.png)
• Ta có: ADHE, ADGF là hình bình hành nên K, I là trung điểm của DE, DF.
• Do đó: $\vec{KI}$ = $\large \frac{1}{2}$$\vec{EF}$ = $\large \frac{1}{2}$($\vec{EG}$ + $\vec{GF}$)
⇒ $\vec{KI}$ = $\large \frac{1}{2}$($\vec{AC}$ - $\vec{FG}$).
• Vậy $\vec{KI}$, $\vec{AC}$, $\vec{FC}$ đồng phẳng.
