Chương II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
§1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
I. TÓM TẮT LÝ THUYẾT:
1. Khái niệm mở đầu:
• Mặt phẳng:
- Mặt bảng, mặt bàn, mặt nước hồ yên lặng cho ta hình ảnh một phần của mặt phẳng. Mặt phẳng không có bề dày và không có giới hạn.
- Để biểu diễn mặt phẳng ta thường dùng hình bình hành hay một miền góc và ghi tên của mặt phẳng vào một góc của hình biểu diễn.
.png)
• Điểm thuộc mặt phẳng:
- Cho điểm A và mặt phẳng ($\alpha$). Khi điểm A thuộc mặt phẳng ($\alpha$) ta nói A nằm trên ($\alpha$) hay ($\alpha$) chứa A, hay ($\alpha$) đi qua A và kí hiệu là A $\in$ ($\alpha$).
- Khi điểm A không thuộc mặt phẳng ($\alpha$) ta nói điểm A nằm ngoài ($\alpha$) hay ($\alpha$) không chứa A và kí hiệu là A $\notin$ ($\alpha$).
• Hình biểu diễn của một hình không gian:
Để nghiên cứu hình học không gian người ta thường vẽ các hình không gian lên bảng, lên giấy. Ta gọi hình vẽ đó là hình biểu diễn của một hình không gian.
2. Các tính chất thừa nhận:
Tính chất 1:
Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
Tính chất 2:
Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
.png)
Tính chất 3:
Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Tính chất 4:
Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
Tính chất 5:
- Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có điểm chung khác nữa.
- Từ đó suy ra: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy.
Tính chất 6:
Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
3. Cách xác định một mặt phẳng:
* Ba cách xác định mặt phẳng:
• Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.
.png)
• Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.
.png)
• Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.
.png)
4. Hình chóp và hình tứ diện:
- Trong mặt phẳng ($\alpha$) cho đa giác lồi $A_{1}A_{2}...A_{n}$. Lấy điểm S nằm ngoài ($\alpha$). Lần lượt nối S với các đỉnh $A_{1},A_{2},...A_{n}$ ta được n tam giác $SA_{1}A_{2}$, $SA_{2}A_{3}$,..., $SA_{n}A_{1}$. Hình gồm đa giác $A_{1}A_{2}...A_{n}$ và n tam giác $SA_{1}A_{2}$, $SA_{2}A_{3}$,..., $SA_{n}A_{1}$ gọi là hình chóp, kí hiệu là S.$A_{1}A_{2}...A_{n}$. Ta gọi S là đỉnh và đa giác $A_{1}A_{2}...A_{n}$ là mặt đáy. Các tam giác $SA_{1}A_{2}$, $SA_{2}A_{3}$,..., $SA_{n}A_{1}$ được gọi là các mặt bên; các đoạn $SA_{1}$, $SA_{2}$,..., $SA_{n}$ là các cạnh bên; các cạnh của đa giác đáy gọi là các cạnh đáy của hình chóp. Ta gọi hình chóp có đáy là tam giác, tứ giác, ngũ giác,...lần lượt là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,...(h.2.24).
.png)
- Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD gọi là hình tứ diện (hay ngắn gọn là tứ diện) và được kí hiệu là ABCD. Các điểm A, B, C, D gọi là các đỉnh của tứ diện. Các đoạn thẳng AB, BC, CD, DA, CA, BD gọi là các cạnh của tứ diện. Hai cạnh không đi qua một đỉnh gọi là hai cạnh đối diện. Các tam giác ABC, ACD, ABD, BCD gọi là các mặt của tứ diện. Đỉnh không nằm trên một mặt gọi là đỉnh đối diện với mặt đó.
- Hình tứ diện có bốn mặt là các tam giác đều gọi là hình tứ diện đều.
• Thiết diện:
Nếu mặt phẳng ($\alpha$) cắt một hình chóp thì ($\alpha$) cắt mặt của hình chóp (hoặc mặt bên hoặc mặt đáy) theo các đoạn thẳng mà ta gọi là các đoạn giao tuyến (Hình vẽ). Nối các đoạn giao tuyến ta được miền đa giác phẳng H . Người ta gọi H là thiết diện của hình chóp cắt bởi mp ($\alpha$).
.png)
II. TRẢ LỜI CÂU HỎI SÁCH GIÁO KHOA:
1. Hãy vẽ thêm một vài hình biểu diễn của hình chóp tam giác.
BÀI GIẢI
.png)
2. Tại sao người thợ mộc kiểm tra độ phẳng mặt bàn bằng cách vẽ thước thẳng trên mặt bàn?
.png)
BÀI GIẢI
• Người thợ mộc đã áp dụng tính chất: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
3. Cho tam giác ABC, M là điểm thuộc phần kéo dài của đoạn BC (hvẽ). Hãy cho biết M có thuộc mặt phẳng (ABC) không và đường thẳng AM có nằm trong mặt phẳng (ABC) không?
.png)
BÀI GIẢI
• $\left\{\begin{matrix} M\in BC\\ BC\subset (ABC) \end{matrix}\right.$ ⇒ M $\in$ (ABC)
• $\left\{\begin{matrix} M\in (ABC)\\ A\in (ABC) \end{matrix}\right.$ ⇒ AM $\subset$ (ABC)
4. Trong mặt phẳng (P), cho hình bình hành (ABCD). Lấy điểm S nằm ngoài mặt phẳng (P). Hãy chỉ ra một điểm chung của hai mặt phẳng (SAC) và (SBD) khác điểm S (hvẽ).
.png)
BÀI GIẢI
• $\left\{\begin{matrix} I\in AC\\ AC\subset (SAC) \end{matrix}\right.$ ⇒ I $\in$ (SAC) (1)
• $\left\{\begin{matrix} I\in BD\\ BD\subset (SBD) \end{matrix}\right.$ ⇒ I $\in$ (SBD) (2)
• Từ (1) và (2) suy ra I là điểm chung của (SAC) và (SBD).
5. Hình 2.16 đúng hay sai? Tại sao?
.png)
BÀI GIẢI
Giao tuyến của hai mặt phẳng phải là một đường thẳng, hình 2.16 sai vì M, K, L không thẳng hàng.
6. Kể tên các mặt bên, cạnh bên, cạnh đáy ở hình 2.24.
.png)
BÀI GIẢI
Mặt bên: SAB, SBC, SCA. Cạnh bên: SA, SB, SC. Cạnh đáy: AB, BC, CA.
III.GIẢI BÀI TẬP SÁCH GIÁO KHOA:
1. Cho điểm A không nằm trên mặt phẳng ($\alpha$) chứa tam giác BCD. Lấy E, F là các điểm lần lượt nằm trên các cạnh AB, AC.
a) Chứng minh đường thẳng EF nằm trong mặt phẳng (ABC).
b) Khi EF và BC cắt nhau tại I, chứng minh I là điểm chung của hai mặt phẳng (BCD) và (DEF).
BÀI GIẢI
.png)
a) Chứng minh EF $\subset$ mp (ABC).
• E $\in$ AB $\subset$ mp (ABC)⇒ E $\in$ mp (ABC) (1)
• F $\in$ AC $\subset$ mp (ABC) ⇒ F $\in$ mp (ABC) (2)
• Từ (1) và (2) ⇒ EFC $\subset$ mp (ABC).
b) Chứng minh I $\in$ mp (BCD) $\cap$ mp (DEF).
• I $\in$ BC $\subset$ mp (BCD) ⇒ I $\in$ mp (BCD) (3)
• I $\in$ EF $\subset$ mp (DEF) ⇒ I $\in$ mp (DEF) (4)
• Từ (3) và (4) ⇒ là điểm chung của hai mặt phẳng (BCD) và (DEF).
2. Gọi M là giao điểm của đường thẳng d và mặt phẳng ($\alpha$). Chứng minh M là điểm chung của ($\alpha$) với một mặt phẳng bất kì chứa d.
BÀI GIẢI
.png)
- Gọi $\beta$ là mặt phẳng bất kì chứa d.
- Ta có d $\cap$ $\alpha$ = M ⇒ $\left\{\begin{matrix} M\in \alpha \\ M\in d\Rightarrow M\in \beta \end{matrix}\right.$
- Vậy M $\in \alpha$ $\cap$ $\beta$.
3. Cho ba đường thẳng $d_{1}$, $d_{2}$, $d_{3}$ không cùng nằm trong một mặt phẳng và cắt từng đôi một. Chứng minh ba đường thẳng trên đồng quy.
BÀI GIẢI
.png)
- Gọi $d_{1}$, $d_{2}$, $d_{3}$ là ba đường thẳng đã cho.
- Gọi l = $d_{1}$ $\cap$ $d_{2}$. Ta chứng minh l $\in$ $d_{3}$.
• I $\in$ $d_{1}$ ⇒ I $\in$ ($\beta$) = ($d_{1}$, $d_{3}$)
• I $\in$ $d_{2}$ ⇒ I $\in$ ($\gamma$) = ($d_{2}$, $d_{3}$).
- Từ đó suy ra I $\in$ $d_{3}$.
4. Cho bốn điểm A, B, C và D không đồng phẳng. Gọi $G_{A}$, $G_{B}$, $G_{C}$, $G_{D}$ lần lượt là trọng tâm của các tam giác BCD, CDA, ABD, ABC. Chứng minh rằng $AG_{A}$, $BG_{B}$, $CG_{C}$, $DG_{D}$ đồng quy.
BÀI GIẢI
.png)
- Gọi M, N, P là trung điểm của CD, DB, BC.
- Trong mp(MAB): $AG_{A}$ $\cap$ $BG_{B}$ = I.
- Ta có: $\large \frac{MB}{MG_{A}}=\frac{MA}{MG_{B}}=3$ ⇒ BA // $G_{A}G_{B}$
- Vậy $\Delta$IAB đồng dạng với $\Delta IG_{A}G_{B}$.
⇒ $\large \frac{IA}{IG_{A}}=\frac{IB}{IG_{B}}=\frac{AB}{G_{A}G_{B}}$ (1)
- Ta lại có $\Delta$MAB đồng dạng với $\Delta$$MG_{B}G_{A}$
⇒ $\large \frac{AB}{G_{A}G_{B}}=\frac{MA}{MG_{B}}=3$ (2)
- Từ (1) và (2), ta có: $\large \frac{IA}{IG_{A}}=\frac{IB}{IG_{B}}=3$
- Chứng minh tương tự, ta cũng có:
$\large \frac{IB}{IG_{B}}=\frac{IC}{IG_{C}}=3$ và $\large \frac{IC}{IG_{C}}=\frac{ID}{IG_{D}}=3$
- Vậy các đường trên đồng quy tại điểm xác định I.
5. Cho tứ giác ABCD nằm trong mặt phẳng ($\alpha$) có hai cạnh AB và CD không song song. Gọi S là điểm nằm ngoài mặt phẳng ($\alpha$) và M là trung điểm đoạn SC.
a) Tìm giao điểm N của đường thẳng SD và mặt phẳng (MAB).
b) Gọi O là giao điểm của AC và BD. Chứng minh rằng ba đường thẳng SO, AM, BN đồng quy.
BÀI GIẢI
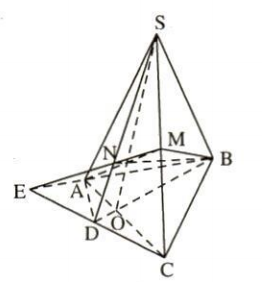
a) Gọi E = CD $\cap$ AB ⇒ E $\in$ (SCD) $\cap$ (MAB) và M $\in$ (SCD) $\cap$ (MAB).
⇒ ME = (SCD) $\cap$ (MAB).
- Trong mặt phẳng (SCD), gọi N = SD $\cap$ ME.
- Khi đó: N = SD $\cap$ (MAB).
b) Gọi I = NB $\cap$ MA
⇒ $\left\{\begin{matrix} I\in NB\subset (SBD)\\ I\in MA\subset (SAC) \end{matrix}\right.$
⇒ I là điểm chung của (SAC) và (SBD).
- Mặt khác: (SAC) $\cap$ (SBD) = SO ⇒ I $\in$ SO.
- Vậy: NA, MA, SO đồng quy.
6. Cho bốn điểm A, B, C và D không đồng phẳng. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD.
a) Tìm giao điểm của đường thẳng CD và mặt phẳng (MNP).
b) Tìm giao tuyến của hai mặt phẳng (MNP) và (ACD).
BÀI GIẢI
.png)
a) Giao điểm của đường thẳng CD với mp (MNP).
• Trong mp (BCD), NP cắt CD tại Q.
• Ta có: $\left\{\begin{matrix} Q\in CD\\ Q\in NP\subset mp(MNP)\Rightarrow Q\in mp(MNP) \end{matrix}\right.$
• Vậy Q = CD $\cap$ mp (MNP).
b) Giao tuyến của mp (MNP) và mp(ACD).
M $\in$ AC $\subset$ (ACD)
.png)
• Vậy MQ = (ACD) $\cap$ (MNP).
7. Cho bốn điểm A, B, C và D không đồng phẳng. Gọi I, K lần lượt là trung điểm của hai đoạn thẳng AD và BC.
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD).
b) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN).
BÀI GIẢI
.png)
a)
• .png)
• .png)
• Vậy IK = (IBC) $\cap$ (KAD).
b) Trong mp (ABC), MN cắt BC tại L.
• .png)
- Trong mp (ABD), DM cắt BI tại P.
• .png)
- Vậy PL = (IBC) $\cap$ (DMN).
8. Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD, trên cạnh AD lấy điểm P không trùng với trung điểm của AD.
a) Gọi E là giao điểm của đường thẳng MP và đường thẳng BD. Tìm giao tuyến của hai mặt phẳng (PMN) và (BCD).
b) Tìm giao điểm của mặt phẳng (PMN) và BC.
BÀI GIẢI
.png)
a) Ta có: E = MP $\cap$ BD ⇒ $\left\{\begin{matrix} E\in MP\subset (PMN)\\ E\in BD\subset (BCD) \end{matrix}\right.$
⇒ E là điểm chung của (PMN) và (BCD).
- Mặt khác: $\left\{\begin{matrix} N\in CD\subset (BCD)\\ N\in (MNP) \end{matrix}\right.$
⇒ N là điểm chung của (PMN) và (BCD).
- Vậy giao tuyến của (PMN) và (BCD) là đường thẳng NE.
b) Trong mp (BCD), gọi Q = EN $\cap$ BC.
- Khi đó: $\left\{\begin{matrix} Q\in EN\subset (MNP)\\ Q\in BC \end{matrix}\right.$ ⇒ Q là giao điểm của BC và (PMN).
- Vậy giao điểm của (PMN) và BC là Q.
9. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng (ABCD) vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt BC tại E. Gọi C' là một điểm nằm trên cạnh SC.
a) Tìm giao điểm M của CD và mp (C'AE).
b) Tìm thiết diện của hình chóp cắt bởi mp (C'AF).
BÀI GIẢI
.png)
a) Vì d không song song với các cạnh của hình bình hành ABCD nên d cắt CD.
• Trong mp (ABCD) gọi M = d $\cap$ CD = AE $\cap$ CD
⇒ $\left\{\begin{matrix} M\in AE\subset (AEC')\\ M\in CD \end{matrix}\right.$
• Vậy M = CD $\cap$ (C'AE).
b) Trong mp (SCD), gọi N = MC' $\cap$ SD. Khi đó giao điểm của (C'AE) với các cạnh BC, SC, SD lần lượt là: E, C', N. Từ đó suy ra:
(C'AE) $\cap$ (ABCD) = AE.
(C'AE) $\cap$ (SBC) = EC'.
(C'AE) $\cap$ (SCD) = C'N.
(C'AE) $\cap$ (SDA) = NA.
• Vậy thiết diện của hình chóp cắt bởi mp (C'AE) là tứ giác AEC'N.
10. Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD.
a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM).
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC).
c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC).
d) Tìm giao điểm P của SC và mặt phẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM).
BÀI GIẢI
.png)
a) Trong mp (SCD), SM cắt CD tại N, ta có:
• N $\in$ CD.
• N $\in$ SM $\subset$ (SBM) ⇒ N $\in$ (SBM).
- Vậy N là giao điểm của đường thẳng CD và mp (SBM).
b) Trong mp (SCD), SM cắt CD tại N.
- Trong mp (ABCD), BN cắt AC tại J.
- Ta có: $\left\{\begin{matrix} J\in BN\subset mp(SBM)\\ J\in AC\subset mp(SAC) \end{matrix}\right.$ ⇒ $J\in mp(SBM)\cap mp(SAC)$
- Vậy mp (SBM) $\cap$ mp (SAC) = SJ.
c) Trong mp (SBN), BM cắt SJ tại I, ta có:
$\left\{\begin{matrix} I\in SJ\subset (SAC)\\ I\in BM \end{matrix}\right.$ ⇒ I $\in$ mp (SAC)
- Vậy I = BM $\cap$ mp (SAC).
d) Trong mp (SAC), AI cắt SC tại P, ta có: P $\in$ SC (1)
- Ta có I là giao điểm của BM và SJ nên I $\in$ BM ⇒ I $\in$ (ABM) ⇒ AI $\subset$ (ABM).
- Mà P $\in$ AI nên P $\in$ (ABM) (2)
- Từ (1) và (2) ⇒ Giao điểm của SC và (ABM) là P.
• $\left\{\begin{matrix} P\in SC\Rightarrow P\in (SCD)\\ P\in (ABM) \end{matrix}\right.$ ⇒ P $\in$ (SCD) $\cap$ (ABM)
• M $\in$ (SCD) $\cap$ (ABM).
- Vậy giao tuyến của hai mặt phẳng (SCD) và (ABM) là đường thẳng PM.
