§3. ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG

I. TÓM TẮT LÝ THUYẾT:

1. Vị trí tương đối của đường thẳng và mặt phẳng:

Cho đường thẳng d và mặt phẳng ($\alpha$), giữa d và ($\alpha$) có 3 vị trí tương đối sau:

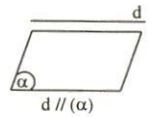
• d song song với $\alpha$:

Khi d và ($\alpha$) không có điểm chung:

d // $\alpha$ ⇔ dn $\cap$ ($\alpha$) = Ø.

• d cắt ($\alpha$):

Khi d và ($\alpha$) chỉ có một điểm chung duy nhất:

d cắt ($\alpha$) ⇔ $\exists$!M: d $\cap$ ($\alpha$) = {M}.

• d nằm trong ($\alpha$) (hay ($\alpha$) chứa d): Khi d và ($\alpha$) có từ 2 điểm chung trở lên.

2. Tính chất:

• Định lý 1:

Nếu đường thẳng d không nằm trên mp ($\alpha$) và song song với đường thẳng d' $\subset$ ($\alpha$) thì d // ($\alpha$).

• Định lý 2:

- Cho đường thẳng a song song với mặt phẳng ($\alpha$). Nếu mp ($\beta$) chứa a và cắt mp ($\alpha$) theo giao tuyến b thì b // a.

- Định lý 2 áp dụng để chứng minh hai đường thẳng song song.

• Hệ quả:

Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

• Định lý 3:

Cho hai đường thẳng chéo nhau có duy nhất một mặt phẳng chứa đường này và song song với đường thẳng kia.

+ a và b chéo nhau.

⇒ Tồn tại duy nhất mp ($\alpha$) $\supset$ a và mp ($\alpha$) // b.

II. TRẢ LỜI CÂU HỎI SÁCH GIÁO KHOA:

1. Trong phòng học hãy quan sát hình ảnh của đường thẳng song song với mặt phẳng.

BÀI GIẢI

• Học sinh tự làm.

2. Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, AC, AD. Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD) không?

BÀI GIẢI

• Tam giác ABC có MN là đường trung bình nên MN // BC.

Mà BC $\subset$ (BCD)

Vậy MN // (BCD).

• Tam giác ABD có MP là đường trung bình nên MP // BD.

Mà BD $\subset$ (BCD)

Vậy MP // (BCD).

• Tam giác ACD có NP là đường trung bình nên NP // CD.

Mà CD $\subset$ (BCD)

Vậy NP // (BCD).

III.GIẢI BÀI TẬP SÁCH GIÁO KHOA:

1. Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.

a) Gọi O và O' lần lượt là tâm của các hình bình hành ABCD và ABEF. Chứng minh rằng đường thẳng OO' song song với các mặt phẳng (ADF) và (BCE).

b) Gọi M và N lần lượt là trọng tâm của hai tam giác ABD và ABE. Chứng minh đường thẳng MN song song với mặt phẳng (CEF).

BÀI GIẢI

a) Tam giác ACE có OO' là đường trung bình

⇒ OO' // CE

Mà CE $\subset$ (BCE).

Vậy OO' // (BCE).

• Tam giác BDF có OO' là đường trung bình

⇒ OO' // DF.

Mà DF $\subset$ (ADF) ⇒ OO' // (ADF).

b) Gọi P là trung điểm AB.

• M là trọng tâm tam giác ABD nên DM đi qua P và $\large \frac{PM}{PD}$ = $\large \frac{1}{3}$ (1)

• N là trọng tâm tam giác ABE nên EN đi qua P và $\large \frac{PN}{PE}$ = $\large \frac{1}{3}$ (2)

• Từ (1), (2) ⇒ $\large \frac{PM}{PD}$ = $\large \frac{PN}{PE}$ = $\large \frac{1}{3}$ ⇒ MN // DE.

• Mà MN không nằm trong (CDFE) và DE $\subset$ (CDFE).

⇒ MN // (CDFE) hay MN // (CEF).

• Vậy MN // (CEF).

2. Cho tứ diện ABCD. Trên cạnh AB lấy một điểm M. Cho ($\alpha$) là mặt phẳng qua M, song song với hai đường thẳng AC và BD.

a) Tìm giao tuyến của ($\alpha$) với các mặt của tứ diện.

b) Thiết diện của tứ diện cắt bởi mặt phẳng ($\alpha$) là hình gì?

BÀI GIẢI

a) Tìm giao tuyến của ($\alpha$) với các mặt của tứ diện.

• Ta có: ($\alpha$) là mặt phẳng qua điểm M.

M $\in$ AB $\subset$ (ABD) ⇒ M $\in$ (ABD)

⇒ M là điểm chung của ($\alpha$) và (ABD).

• Mà ($\alpha$) // BD (giả thiết)

⇒ ($\alpha$) cắt (ABD) theo giao tuyến qua M và song song với BD.

• Trong (ABD), đường thẳng qua M và song song với BD cắt AD tại N.

⇒ ($\alpha$) $\cap$ (ABD) = MN.

• Mặt khác, ta có:

⇒ ($\alpha$) $\cap$ (BCD) = PQ.

b) Thiết diện của tứ diện cắt bởi ($\alpha$) là hình gì?

• Theo câu a ta có:

($\alpha$) $\cap$ (ABD) = MN.

($\alpha$) $\cap$ (ACD) = NP.

($\alpha$) $\cap$ (BCD) = PQ.

($\alpha$) $\cap$ (ABC) = QM.

⇒ Thiết diện của tứ diện cắt bởi ($\alpha$) là tứ giác MNPQ.

• Mặt khác, ta có:

• Từ (1) và (2) ⇒ Tứ giác MNPQ là hình bình hành.

• Vậy thiết diện của tứ diện cắt bởi mặt phẳng ($\alpha$) là hình bình hành MNPQ.

3. Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng ($\alpha$) đi qua O, song song với AB và SC. Thiết diện đó là hình gì?

BÀI GIẢI

- Ta có: O = AC $\cap$ BD ⇒ O $\in$ (ABCD)

- Theo giả thiết $\left\{\begin{matrix} (\alpha )//AB\\ O\in (\alpha ) \end{matrix}\right.$

⇒ ($\alpha$) cắt (ABCD) theo giao tuyến qua O và song song với AB.

- Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại M và N.

⇒ ($\alpha$) $\cap$ (ABCD) = MN // AB (1)

- Gọi P = Nx $\cap$ SB ⇒ ($\alpha$) $\cap$ (SBC) = NP // SC. (2)

- Gọi Q = Py $\cap$ SA ⇒ ($\alpha$) $\cap$ (SAB) = PQ // AB. (3)

- Ta lại có: ($\alpha$) $\cap$ (SAD) = QM. (4)

• Từ (1), (2), (3) và (4) ⇒ Thiết diện của hình chóp cắt bởi ($\alpha$) là tứ giác MNPQ.

- Mặt khác, do $\left\{\begin{matrix} MN//AB\\ PQ//AB \end{matrix}\right.$ ⇒ MN // PQ

⇒ MNPQ là hình thang.

- Vậy thiết diện của hình chóp cắt bởi ($\alpha$) là hình thang MNPQ.