CÂU HỎI TRẮC NGHIỆM CHƯƠNG 3
1. Trong các mệnh đề sau đây, mệnh đề nào là đúng?
(A) Từ $\vec{AB}$ = 3$\vec{AC}$ ta suy ra $\vec{BA}$ = -3$\vec{CA}$.
(B) Từ $\vec{AB}$ = -3$\vec{AC}$ ta suy ra $\vec{CB}$ = 2$\vec{AC}$.
(C) Vì $\vec{AB}$ = -2$\vec{AC}$ + 5$\vec{AD}$ nên bốn điểm A, B, C, D cùng thuộc một mặt phẳng.
BÀI GIẢI
• Câu A sai, đúng là $\vec{AB}$ = 3$\vec{AC}$ ⇒ $\vec{BA}$ = 3$\vec{CA}$.
• Câu B sai, đúng là $\vec{AB}$ = -3$\vec{AC}$ ⇔ $\vec{AC}$ + $\vec{CB}$ = -3$\vec{AC}$ ⇔ $\vec{CB}$ = -4$\vec{AC}$.
• Câu C đúng vì $\vec{AB}$ = -2$\vec{AC}$ + 5$\vec{AD}$.
⇒ $\vec{AB}$, $\vec{AC}$, $\vec{AD}$ đồng phẳng ⇒ A, B, C, D cùng thuộc một mặt phẳng.
• Câu D sai, đúng là $\vec{AB}$ = -$\large \frac{1}{2}$$\vec{BC}$ ⇔ $\vec{AB}$ = $\large \frac{1}{2}$$\vec{CB}$.
⇒ A là trung điểm của đoạn CB
2. Tìm mệnh đề sai trong các mệnh đề sau đây:
(A) Vì $\vec{NM}$ + $\vec{NP}$ = $\vec{0}$ nên N là trung điểm của đoạn MP.
(B) Vì I là trung điểm của đoạn AB nên từ một điểm O bất kì ta có:
$\vec{OI}$ = $\large \frac{1}{2}$($\vec{OA}$ + $\vec{OB}$).
(C) Từ hệ thức $\vec{AB}$ = 2$\vec{AC}$ - 8$\vec{AD}$ ta suy ra ba vectơ $\vec{AB}$, $\vec{AC}$, $\vec{AD}$ đồng phẳng.
(D) Vì $\vec{AB}$ + $\vec{BC}$ + $\vec{CD}$ + $\vec{DA}$ = $\vec{0}$ nên bốn điểm A, B, C, D cùng thuộc một mặt phẳng.
BÀI GIẢI
(A) Mệnh đề (A) đúng vì N là trung điểm của đoạn MP thì:
$\vec{NM}$ = - $\vec{NP}$ ⇒ $\vec{NM}$ + $\vec{NP}$ = $\vec{0}$.
(B) Mệnh đề (B) đúng.
$\vec{OI}$ = $\vec{OA}$ + $\vec{AI}$
$\vec{OI}$ = $\vec{OB}$ + $\vec{BI}$
⇒ 2$\vec{OI}$ = $\vec{OA}$ + $\vec{OB}$ + ($\vec{AI}$ + $\vec{BI}$).
• Vì I là trung điểm của đoạn thẳng AB nên: $\vec{AI}$ + $\vec{BI}$ = $\vec{0}$.
Vậy 2$\vec{OI}$ = $\vec{OA}$ + $\vec{OB}$.
(C) Mệnh đề (C) đúng.
(D) Mệnh đề (D) sai.
Vì $\vec{AB}$ + $\vec{BC}$ + $\vec{CD}$ + $\vec{DA}$ = $\vec{0}$ đúng với mọi điểm A, B, C, D
⇔ $\vec{AC}$ + $\vec{CA}$ = $\vec{AA}$.
Nên kết luận A, B, C, D cùng thuộc một mặt phẳng là sai.
3. Trong các kết quả sau đây, kết quả nào đúng?
Cho hình lập phương ABCD.EFGH có cạnh a. Ta có $\vec{AB}$.$\vec{EG}$ bằng:
(A) $a^{2}$;
(B) $a^{2}\sqrt{2}$;
(C) $a^{2}\sqrt{3}$;
(D) $\large \frac{a^{2}\sqrt{2}}{2}$
BÀI GIẢI
.png)
• Vì $\vec{EG}$ = $\vec{AC}$ nên:
$\vec{AB}$.$\vec{EG}$ = $\vec{AB}$.$\vec{AC}$
= AB.AC. cos($\vec{AB}$, $\vec{AC}$)
= a.a$\sqrt{2}$.cos 45° = $a^{2}$ (câu A đúng).
4. Trong các mệnh đề sau đây, mệnh đề nào đúng?
(A) Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì a vuông góc với c.
(B) Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b song song với đường thẳng c thì a vuông góc với c.
(C) Cho ba đường thẳng a, b, c vuông góc với nhau từng đôi một. Nếu có một đường thẳng d vuông góc với a thì d song song với b hoặc c.
(D) Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c vuông góc với a thì c vuông góc với mọi đường thẳng nằm trong mặt phẳng (a, b).
BÀI GIẢI
(A) Sai, vì a, c cùng vuông góc với b thì a, c không nhất thiết phải vuông góc.
(B) Đúng, vì $\left\{\begin{matrix} a\perp b\\ b//c \end{matrix}\right.$ ⇒ (a,c) = (a, b) = 90° ⇒ a $\perp$ c.
5. Trong các mệnh đề sau đây, hãy tìm mệnh đề đúng:
(A) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
(B) Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ vuông góc với mặt phẳng kia.
(C) Hai mặt phẳng ($\alpha$) và ($\beta$) vuông góc với nhau và cắt nhau theo giao tuyến d. Với mỗi điểm A thuộc ($\alpha$) và mỗi điểm B thuộc ($\beta$) thì ta có đường thẳng AB vuông góc với d.
(D) Nếu hai mặt phẳng ($\alpha$) và ($\beta$) đều vuông góc với mặt phẳng ($\gamma$) thì giao tuyến d của ($\alpha$) và ($\beta$) nếu có sẽ vuông góc với ($\gamma$).
BÀI GIẢI
(A) Sai, vì a, c cùng vuông góc với b thì a, c không nhất thiết phải vuông góc.
(B) Đúng, vì c và b song song với nhau nên góc giữa a và c bằng góc giữa a và b mà a $\perp$ b ⇒ a $\perp$ c.
(C) Sai, vì chỉ có thể kết luận được AB, d không đồng phẳng.
(D) Đúng.
6. Tìm các mệnh đề sai trong các mệnh để sau đây:
(A) Hai đường thẳng a và b trong không gian có các vectơ chỉ phương lần lượt là $\vec{u}$ và $\vec{v}$. Điều kiện cần và đủ để a và b chéo nhau là a và b không có điểm chung và hai vectơ $\vec{u}$, $\vec{v}$ không cùng phương.
(B) Cho a, b là hai đường thẳng chéo nhau và vuông góc với nhau. Đường vuông góc chung của a và b nằm trong mặt phẳng chứa đường này và vuông góc với đường kia.
(C) Không thể có một hình chóp tứ giác S.ABCD nào có hai mặt bên (SAB) và (SCD) cùng vuông góc với mặt phẳng đáy.
(D) Cho $\vec{u}$, $\vec{v}$ là hai vectơ chỉ phương của hai đường thẳng cắt nhau nằm trong mặt phẳng ($\alpha$) và $\vec{n}$ là vectơ chỉ phương của đường thẳng $\Delta$. Điều kiện cần và đủ để $\Delta$ $\perp$ ($\alpha$) là $\vec{n}$.$\vec{u}$ = 0 và $\vec{n}$.$\vec{v}$ = 0.
BÀI GIẢI
(A) Từ giả thiết a và b không có điểm chung và các vectơ chỉ phương $\vec{u}$, $\vec{v}$ của chúng không cùng phương ta suy ra hai đường thẳng a, b không đồng phẳng vì chúng không trùng nhau, không cắt nhau, không song song với nhau, vậy a và b chéo nhau. Ngược lại nếu a và b chéo nhau thì rõ ràng là a và b không có điểm chung và $\vec{u}$, $\vec{v}$ không cùng phương.
Mệnh đề A đúng.
(B) a và b có đường vuông góc chung là c; a $\perp$ b
Ta có: $\left\{\begin{matrix} a\perp b\\ a\perp c \end{matrix}\right.$ ⇒ a $\perp$ (b;c)
Tương tự ta có: $\left\{\begin{matrix} b\perp a\\ b\perp c \end{matrix}\right.$ ⇒ b $\perp$ (a;c)
Mệnh đề B đúng.
(C) Xét trường hợp AB và CD cắt nhau tại một điểm H.
Ta lấy S trên đường vuông góc với mp(ABCD) kẻ từ H thì rõ ràng:
(SAB) $\perp$ (ABCD) và (SCD) $\perp$ (ABCD).
Thật vậy:
• (SAB) $\supset$ SH mà SH $\perp$ (ABCD) ⇒ (SAB) $\perp$ (ABCD).
• (SCD) $\supset$ SH mà SH $\perp$ (ABCD) ⇒ (SCD) $\perp$ (ABCD).
(D) Đúng.
.png)
7. Trong các mệnh đề sau đây, mệnh đề nào là đúng?
(A) Một đường thẳng cắt hai đường thẳng cho trước thì cả ba đường thẳng đó cùng nằm trong một mặt phẳng.
(B) Một đường thẳng cắt hai đường thẳng cắt nhau cho trước thì cả ba đường thẳng đó cùng nằm trong một mặt phẳng.
(C) Ba đường thẳng cắt nhau từng đôi một thì cùng nằm trong một mặt phẳng.
(D) Ba đường thẳng cắt nhau từng đôi một và không nằm trong một mặt phẳng thì đồng quy.
BÀI GIẢI
(A) Sai, chẳng hạn đường thẳng đó là đường vuông góc chung.
(B) Sai, vì nếu đường thẳng thứ ba đi qua giao điểm của hai đường thẳng đã cho thì xảy ra trường hợp cả ba đường thẳng không cùng nằm trong một mặt phẳng.
(C) Sai, (như trường hợp B).
(D) Đúng.
8. Trong các mệnh đề sau, mệnh đề nào là đúng?
(A) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
(B) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
(C) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
(D) Hai đường thẳng không cắt nhau và không song song thì chéo nhau.
BÀI GIẢI
(A) Đúng.
(B) Sai, vì hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vẫn có thể cắt nhau.
(C) Sai, vì chỉ đúng khi hai đường thẳng vuông góc với mặt phẳng.
(D) Sai, vì hai đường thẳng đó trùng nhau hoặc chéo nhau.
9. Trong các mệnh đề sau, mệnh đề nào là đúng?
(A) Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
(B) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.
(C) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.
(D) Một mặt phẳng ($\alpha$) và một đường thẳng a không thuộc ($\alpha$) cùng vuông góc với đường thẳng b thì ($\alpha$) song song với a.
BÀI GIẢI
(A) Sai, vì hai đường thẳng cắt nhau, chéo nhau cũng song song được với một mặt phẳng.
(B) Sai, vì hai mặt phẳng song song cũng vuông góc được với một mặt phẳng.
(C) Sai, vì trong không gian hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng có thể cắt nhau.
(D) Đúng.
10. Tìm mệnh đề đúng trong các mệnh đề sau đây:
(A) Đoạn vuông góc chung của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì lần lượt nằm trên hai đường thẳng ấy và ngược lại.
(B) Qua một điểm cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
(C) Qua một điểm cho trước có duy nhất một đường thẳng vuông góc với một đường thẳng cho trước.
(D) Cho ba đường thẳng a, b, c chéo nhau từng đôi một. Khi đó ba đường thẳng này sẽ nằm trong ba mặt phẳng song song với nhau từng đôi một.
BÀI GIẢI
(A) Đúng.
(B) Sai. Vì qua một điểm cho trước ta có thể dựng vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
(C) Sai. Qua một điểm cho trước có thể kẻ vô số đường thẳng vuông góc với đường thẳng a cho trước, các đường thẳng này nằm trong mặt phẳng đi qua điểm đã cho và vuông góc với đường thẳng a.
(D) Sai. Chỉ đúng trong trường hợp hai đường thẳng chéo nhau.
11. Khoảng cách giữa hai cạnh đối của một tứ diện đều cạnh a bằng kết quả nào trong các kết quả sau đây?
(A) $\large \frac{3a}{2}$
(B) $\large \frac{a\sqrt{2}}{2}$
(C) $\large \frac{a\sqrt{3}}{2}$
(D) $a\sqrt{2}$
BÀI GIẢI
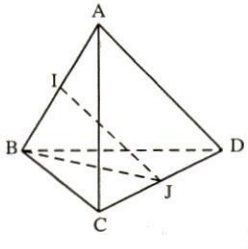
• Gọi I là trung điểm cạnh AB.
J là trung điểm cạnh CD.
• IJ là đoạn vuông góc chung của AB, CD. Độ dài của IJ là khoảng cách giữa hai cạnh đối AB, CD của tứ diện.
• Ta có: BC = BD (gt).
⇒ $\Delta$BCD cân tại B, ta có:
BJ là trung tuyến cũng là đường cao
⇒ BJ $\perp$ CD và CJ = $\large \frac{a}{2}$.
⇒ $\Delta$BJC vuông tại J, ta có:
$BJ^{2}$ = $BC^{2}$ - $CJ^{2}$
.png)
• Xét $\Delta$BIJ vuông tại I, ta có:
.png)
Vậy B đúng.
