§5. KHOẢNG CÁCH
I. TÓM TẮT LÝ THUYẾT:
1. Khoảng cách từ một điểm đến một đường thẳng:
Định nghĩa:
Trong không gian cho điểm O và đường thẳng a. Qua O dựng mặt phẳng vuông góc với a, mặt phẳng này cắt a tại H. Độ dài đoạn thẳng OH được gọi là khoảng cách từ điểm O đến đường thẳng a.
.png)
2. Khoảng cách từ một điểm đến một mặt phẳng:
Định nghĩa:
Khoảng cách từ điểm O đến mặt phẳng $\alpha$ là độ dài đoạn thẳng nối O với hình chiếu H của O trên mặt phẳng ($\alpha$).
.png)
3. Khoảng cách giữa đường thẳng và mặt phẳng song song:
• Cho đường thẳng a // mp($\alpha$).
• Khoảng cách giữa a và ($\alpha$) là khoảng cách từ một điểm O $\in$ a đến mp($\alpha$).
.png)
4. Khoảng cách giữa hai mặt phẳng song song:
Cho hai mặt phẳng (P) và (Q) song song nhau. Khoảng cách giữa (P) và (Q) là khoảng cách từ một điểm trên (P) đến (Q) hoặc một điểm trên (Q) đến (P).
.png)
5. Đường vuông góc chung và khoảng cách giữa hai đường thẳng chéo nhau:
Định nghĩa:
.png)
a) Đường thẳng $\Delta$ cắt hai đường thẳng chéo nhau a, b và cùng vuông góc với mỗi đường thẳng ấy gọi là đường vuông góc chung của a và b.
b) Nếu đường vuông góc chung $\Delta$ cắt hai đường thẳng chéo nhau a, b lần lượt tại M, N thì độ dài đoạn thẳng MN gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b.
* Cách tìm khoảng cách đường vuông góc chung của hai đường thẳng chéo nhau a, b:
.png)
• Gọi ($\beta$) là mặt phẳng chứa b và song song với a và a' là hình chiếu vuông góc của a trên mặt phẳng đó.
• a' cắt b tại N, khi đó đường thẳng $\Delta$ qua N và vuông góc với ($\beta$) là đường vuông góc chung.
* Nhận xét:
• Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
• Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
.png)
II. GIẢI ĐÁP CÂU HỎI SÁCH GIÁO KHOA:
1. Cho điểm O và đường thẳng a. Chứng minh rằng khoảng cách từ điểm O đến đường thẳng a là bé nhất so với các khoảng cách từ O đến một điểm bất kì của đường thẳng a.
BÀI GIẢI
.png)
• Gọi OH là khoảng cách từ O đến đường thẳng a.
• Xét trong mặt phẳng (O, a), ta lấy một điểm M bất kì trên a và luôn luôn có OM $\geq$ OH (kể cả trường hợp điểm O thuộc a).
2. Cho điểm O và mặt phẳng ($\alpha$). Chứng minh rằng khoảng cách từ điểm O đến mặt phẳng ($\alpha$) là bé nhất so với các khoảng cách từ O tới một điểm bất kì của mặt phẳng ($\alpha$).
BÀI GIẢI
.png)
• Gọi OH là khoảng cách từ O đến mặt phẳng ($\alpha$).
• Lấy điểm M bất kì thuộc mặt phẳng ($\alpha$).
• Theo tính chất cạnh của tam giác vuông.
Ta có OH $\leq$ OM, $\forall$M $\in$ ($\alpha$).
3. Cho đường thẳng a song song với mặt phẳng ($\alpha$). Chứng minh rằng khoảng cách giữa đường thẳng a và mặt phẳng ($\alpha$) là bé nhất so với khoảng cách từ một điểm bất kì của mặt phẳng này tới một điểm bất kì của mặt phẳng ($\alpha$).
BÀI GIẢI
.png)
• Gọi AH là khoảng cách từ điểm A đến mặt phẳng ($\alpha$).
• M là điểm thuộc mặt phẳng ($\alpha$).
• Theo tính chất cạnh của tam giác vuông.
Ta có AH $\leq$ AM, $\forall$M $\in$ ($\alpha$).
4. Cho hai mặt phẳng ($\alpha$) và ($\beta$). Chứng minh rằng khoảng cách giữa hai mặt phẳng song song ($\alpha$) và ($\beta$) là nhỏ nhất trong các khoảng cách từ một điểm bất kì của mặt phẳng này tới một điểm bất kì của mặt phẳng kia.
BÀI GIẢI
.png)
• Ta có: d(($\alpha$), ($\beta$)) = d(M, ($\beta$)) = d(M', ($\alpha$)).
• Lấy N là một điểm bất kì thuộc mặt phẳng ($\beta$)
• Theo tính chất về đường vuông góc và đường xiên trong mặt phẳng, ta có:
MM' $\leq$ MN, $\forall$N $\in$ ($\beta$).
5. Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm của cạnh BC và AD. Chứng minh rằng: MN $\perp$ BC và MN $\perp$ AD.
BÀI GIẢI
.png)
• Ta có hai tam giác ABC và DCB bằng nhau. Do đó hai đường trung tuyến tương ứng cũng bằng nhau là AM = DM. Vậy AMD là tam giác cân tại M và suy ra MN $\perp$ AD.
• Chứng minh tương tự: $\Delta$BAD = $\Delta$CDA (c.c.c)
⇒ Hai đường trung tuyến tương ứng cũng bằng nhau là BN = CN.
Vậy BNC là tam giác cân tại M và suy ra MN $\perp$ AD.
6. Chứng minh rằng khoảng cách giữa hai đường thẳng chéo nhau là bé nhất so với khoảng cách giữa hai điểm bất kì lần lượt nằm trên hai đường thẳng ấy.
BÀI GIẢI
.png)
• Trên hình vẽ ta có: N'N" // a, MM' = N'N".
• Ta chứng minh MN $\perp$ NN".
.png)
⇒ MN $\perp$ (NN'N").
• Mà NN" $\subset$ (NN'N'') ⇒ MN $\perp$ NN".
• $\Delta$MNN" vuông tại N.
• Theo tính chất về đường vuông góc và đường xiên trong mặt phẳng.
Ta có MN $\leq$ MN" ⇒ MN $\leq$ M'N' (do MN" = M'N').
III. GIẢI BÀI TẬP SÁCH GIÁO KHOA:
1. Trong các mệnh đề sau đây, mệnh đề nào đúng?
a) Đường thẳng $\Delta$ là đường vuông góc chung của hai đường thẳng a và b nếu $\Delta$ vuông góc với a và $\Delta$ vuông góc với b.
b) Gọi (P) là mặt phẳng song song với cả hai đường thẳng a, b chéo nhau. Khi đó đường vuông góc chung $\Delta$ của a và b luôn luôn vuông góc với (P).
c) Gọi $\Delta$ là đường vuông góc chung của hai đường thẳng chéo nhau a và b thì $\Delta$ là giao tuyến của hai mặt phẳng (a, $\Delta$) và (b, $\Delta$).
d) Cho hai đường thẳng chéo nhau a và b. Đường thẳng nào đi qua một điểm M trên a đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Đường vuông góc chung của hai đường thẳng chéo nhau a và b nằm trong mặt phẳng chứa đường này và vuông góc với đường kia.
BÀI GIẢI
a) Sai vì đường vuông góc chung của hai đường thẳng a và b không những phải vuông góc với a và b mà còn phải cắt cả a và b.
b) Đúng vì (P) // a thì (P) chứa a’ // a; (P) // b thì (P) chứa b’ // b
$\Delta$ $\perp$ a, a // a' ⇒ $\Delta$ $\perp$ a'
$\Delta$ $\perp$ b, b // b' ⇒ $\Delta$ $\perp$ b'
• a và b chéo nhau nên a' và b' là hai đường thẳng giao nhau của mp (P);
$\Delta$ $\perp$ a', $\Delta$ $\perp$ b' ⇒ $\Delta$ $\perp$ (P).
c) Đúng vì (a, $\Delta$) và (b, $\Delta$) giao nhau theo giao tuyến $\Delta$.
d) Sai vì thiếu điều kiện vuông góc với a.
e) Sai vì chỉ có trường hợp a $\perp$ b thì qua a ta mới có một mặt phẳng vuông góc với b.
2. Cho tứ diện S.ABC có SA vuông góc với mặt phẳng (ABC). Gọi H, K lần lượt là trực tâm của tam giác ABC và SBC.
a) Chứng minh ba đường thẳng AH, SK, BC đồng quy.
b) Chứng minh rằng SC vuông góc với mặt phẳng (BHK) và HK vuông góc với mặt phẳng (SBC).
c) Xác định đường vuông góc chung của BC và SA.
BÀI GIẢI
.png)
a) Gọi I là giao điểm của AH và BC.
Ta có SA $\perp$ (ABC) ⇒ SA $\perp$ BC
.png)
Vậy ba đường thẳng AH, SK, BC đồng quy tại I.
b) Kẻ đường cao BE của tam giác ABC
.png)
• Trong mp (ABC), ta có BE $\perp$ AC.
• Mà AC là giao tuyến của hai mặt phẳng (SAC) và (ABC) nên BH $\perp$ (SAC).
Vì DC $\subset$ (SAC) nên SC $\perp$ BH. (1)
• K là trực tâm của $\Delta$SBC nên BK $\perp$ SC (2)
• Từ (1) và (2) suy ra SC $\perp$ (BHK).
.png)
Và HK $\subset$ (SAI) ⇒ BC $\perp$ HK. (3)
Ta đã có SC $\perp$ (BHK) mà HK $\subset$ (BHK) ⇒ HK $\perp$ SC. (4)
• Từ (3) và (4) suy ra HK $\perp$ (SBC).
c) Vì SA $\perp$ (ABC); mà AI $\subset$ (ABC) ⇒ SA $\perp$ AI. Và AI $\perp$ BC.
• Vậy AI là đường vuông góc chung của SA và BC.
• Mặt khác ta lại có: BH.AC = BH.BC (= 2$S_{ABC}$) ⇒ BH = $\large \frac{BA.BC}{AC}$
.png)
b) Ta có:
.png)
• Mặt phẳng (ACC'A') chính là mặt phẳng chứa A'C' và song song với BB', B là một điểm thuộc BB', do đó khoảng cách BH từ B đến mp(ACC'A') cũng là khoảng cách giữa hai đường thẳng BB' và A'C' và cũng bằng .png)
3. Cho hình lập phương ABCD.A'B'C'D cạnh a. Chứng minh rằng các khoảng cách từ các điểm B, C, D, A', B', d' đến đường chéo AC' đều bằng nhau. Tính khoảng cách đó.
BÀI GIẢI
.png)
• Các tam giác BAC', CA'A, DAC', A'AC', B'C'A, D'C'A bằng nhau nên các đường cao ứng với cạnh AC' bằng nhau.
• Ta có: CC' = a; CA = a$\sqrt{2}$.
.png)
4. Cho hình hộp ABCD. A'B'C'D' có AB = a, BC = b, CC' = c.
a) Tính khoảng cách từ B đến mặt phẳng (ACC'A').
b) Tính khoảng cách giữa hai đường thẳng BB' và AC'.
BÀI GIẢI
.png)
a) Vì AA' $\perp$ (ABCD); AA' $\subset$ (ACC'A') ⇒ (ACC'A') $\perp$ (ABCD).
• Hai mặt phẳng này vuông góc với nhau và cắt nhau theo giao tuyến AC nên nếu từ B ta kẻ BH $\perp$ AC thì: BH $\perp$ (ACC'A').
⇒ BH là khoảng cách từ B đến mp (ACC'A').
Xét tam giác vuông tại B, ta có:
$AC^{2}$ = $AB^{2}$ + $BC^{2}$ ⇒ $AC^{2}$ = $a^{2}$ + $b^{2}$
⇒ AC = $\sqrt{a^{2}+b^{2}}$
5. Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a.
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C').
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD').
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'.
.png)
BÀI GIẢI
a) Chứng minh B'D $\perp$ mp(BA'C')
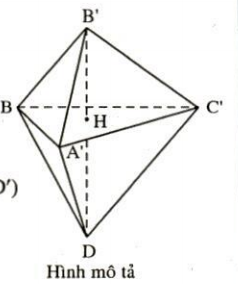
• Ta có:
B'B = B'A' = B'C' = a
AB' = A'C' = C'B = $a\sqrt{2}$ (đường chéo của các hình vuông cạnh bằng a)
⇒ Hình chóp B'.BA'C' là hình chóp đều.
⇒ B'H $\perp$ (BA'C'), H là trực tâm của tam giác đều BA'C'. (1)
• Tương tự D.BA'C' là hình chóp đều.
⇒ DH $\perp$ (BA'C'). (2)
* (1) và (2) ⇒ B'D $\perp$ (BA'C'). (đpcm)
b) Khoảng cách giữa hai mặt phẳng (BA'C') và (ACD')
.png)
* Gọi O' là tâm hình vuông A'B'C'D'.
⇒ O' là trung điểm A'C', B'D'.
* Trong mp (BB'D'D), B'D cắt BO' tại $G_{1}$ mà BO' $\subset$ mp(BA'C') nên $G_{1}$ là giao điểm của B'D với mp (BA'C'). Vậy B'$G_{1}$ $\perp$ mp (BA'C').
⇒ B'$G_{1}$ = khoảng cách từ B' đến mp (BA'C').
* Tương tự, $DG_{2}$ = khoảng cách từ D đến mp (ACD').
* mp(ACD') $\perp$ B'D (cmt)
mp(BA'C') $\perp$ B'D (cmt)
⇒ mp (ACD') // mp (BA'C').
• Vậy $G_{1}G_{2}$ = khoảng cách giữa hai mặt phẳng (ACD') và (BA'C').
* Ta có:
O'$G_{1}$ là đường trung bình của tam giác A'D'$G_{2}$ ⇒ B’$G_{1}$ = $G_{1}G_{2}$.
O$G_{2}$ là đường trung bình của tam giác BD$G_{1}$ ⇒ D$G_{2}$ = $G_{1}G_{2}$.
• Vậy $G_{1}G_{2}$ = B’$G_{1}$ = D$G_{2}$ = $\large \frac{1}{3}$B'D = $\large \frac{a\sqrt{3}}{3}$
• Kết luận khoảng cách giữa hai mặt phẳng (ACD') và (BA'C') bằng $\large \frac{a\sqrt{3}}{3}$
c) Khoảng cách giữa BC' và CD'.
* BC' và CD' chéo nhau.
* BC' $\subset$ mp (BA'C') và CD' $\subset$ mp (ACD').
* mp (BA'C') // mp (ACD').
• Vậy khoảng cách giữa BC' và CD' bằng khoảng cách giữa hai mặt phẳng (BA'C') và (ACD'), đó là $\large \frac{a\sqrt{3}}{3}$
6. Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là đường vuông góc chung của AB và CD thì AC = BD và AD = BC.
BÀI GIẢI
.png)
• Qua điểm K dựng đường thẳng d // AB, mp(d; CD) là mặt phẳng chứa CD và song song với AB.
Ta có: IK $\perp$ AB ⇒ IK $\perp$ d.
Mà IK $\perp$ CD ⇒ IK $\perp$ (d; CD).
• Từ A, B kẻ AA' $\perp$ (d; CD) và BB' $\perp$ (d; CD) ⇒ AA' // IK // BB'.
Và AA' = IK = BB'. (1)
Mà K $\in$ d và d // AB.
Suy ra mọi khoảng cách từ AB đến d đều bằng nhau.
Với A $\in$ AB và B $\in$ AB. Do đó A' $\in$ d và B' $\in$ d.
Xét $\Delta$CA'K và $\Delta$DB'K, có:
CK = CD (K là trung điểm của CD)
$\widehat{CKA'}$ = $\widehat{DKB'}$ (đối đỉnh)
A'K = KB' (vì IA = IB và AA' // IK // BB')
⇒ $\Delta$CA’K = $\Delta$DB'K ⇒ CA' = DB' (2)
• Mặt khác: AA’ $\perp$ (d; CD) $\supset$ CA’ ⇒ AA' $\perp$ CA'.
BB' $\perp$ (d; CD) $\supset$ DB' ⇒ BB' $\perp$ DB'.
• Từ (1) và (2) suy ra hai tam giác vuông CA’A và DB'B bằng nhau.
Nên AC = DB.
Chứng minh tương tự, ta có: AD = BC.
7. Cho hình chóp tam giác đều S.ABC các cạnh đáy bằng 3a, cạnh bên bằng 2a. Tính khoảng cách từ S tới mặt đáy (ABC).
BÀI GIẢI
.png)
• Vì hình chóp S.ABC là hình chóp đều nên nếu kẻ SH $\perp$ (ABC) thì H là tâm đường tròn ngoại tiếp tam giác ABC, M là trung điểm của cạnh BC thì AM = $\large \frac{AB\sqrt{3}}{2}$
⇒ AM = $\large \frac{3a\sqrt{3}}{2}$
Mà AH = $\large \frac{2}{3}$AM ⇒ AH = $\large \frac{2}{3}$. $\large \frac{3a\sqrt{3}}{2}$ = a$\sqrt{3}$.
• Xét tam giác SAH vuông tại H, ta có:
$SH^{2}$ = $SA^{2}$ - $AH^{2}$
⇒ $SH^{2}$ = 4$a^{2}$ - 3$a^{2}$ = $a^{2}$ ⇒ SH = a.
8. Cho tứ diện đều ABCD cạnh a. Tính khoảng cách giữa hai cạnh đối của tứ diện đều đó.
BÀI GIẢI
.png)
• Gọi I, K theo thứ tự là trung điểm của các cạnh AB, CD.
Tam giác ABC cân nên CI $\perp$ AB (1)
Tam giác ACD cân nên DI $\perp$ AB (2)
• Từ (1) và (2) ⇒ AB $\perp$ (DIC) ⇒ AB $\perp$ IK
Tam giác ADC cân nên AK $\perp$ DC (3)
Tam giác BCD cân nên BK $\perp$ DC (4)
• Từ (3) và (4) suy ra DC $\perp$ (AKB)
Mà IK $\subset$ (AKB)
⇒ DC $\perp$ IK
• Vậy IK là đường vuông góc chung của AB, CD và độ dài đoạn thẳng IK là khoảng cách giữa hai đường thẳng AB, CD.
• Ta có: IC = $\large \frac{a\sqrt{3}}{2}$; KC = $\large \frac{a}{2}$
• Xét $\Delta$CIK vuông tại K, ta có:
.png)
