§5. PHÉP QUAY
I. TÓM TẮT LÝ THUYẾT:
1. Định nghĩa:
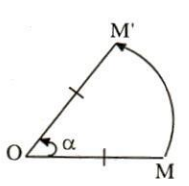
- Cho điểm O và góc lượng giác $\alpha$. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M' sao cho OM' = OM và góc lượng giác (OM; OM') bằng $\alpha$ được gọi là phép quay tâm O góc $\alpha$.
- Điểm O được gọi là tâm quay còn $\alpha$ được gọi là góc quay của phép quay đó.
- Phép quay tâm O góc $\alpha$ thường được kí hiệu là $Q_{(O,\alpha )}$
- Nhận xét:
• Chiều dương của phép quay là chiều dương của đường tròn lượng giác nghĩa là chiều ngược chiều quay của kim đồng hồ.
.png)
• Với k là số nguyên ta luôn có phép quay $Q_{(O,2k\pi )}$ là phép đồng nhất. Phép quay $Q_{(O,(2k+1)\pi )}$ là phép đối xứng tâm O.
2. Tính chất:
Tính chất 1: Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.
.png)
Tính chất 2: Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
.png)
Nhận xét:
Phép quay góc $\alpha$ với 0 < $\alpha$ < $\pi$, biến đường thẳng d thành đường thẳng d' sao cho góc giữa d và d' bằng $\alpha$ (nếu 0 < $\alpha$ $\leq$ $\large \frac{\pi }{2}$), hoặc bằng $\pi -\alpha$ (nếu $\large \frac{\pi }{2}$ $\leq$ $\alpha$ < $\pi$).
.png)
II. GIẢI ĐÁP CÂU HỎI SÁCH GIÁO KHOA:
1. Trong hình 1.29 tìm một góc quay thích hợp để phép quay tâm O:
- Biến điểm A thành điểm B.
- Biến điểm C thành điểm D.
.png)
BÀI GIẢI
• $Q_{(O,45^{0})}$ biến A thành B; $Q_{(O,60^{0})}$ biến C thành D.
2. Trong hình 1.31 khi bánh xe A quay theo chiều dương thì bánh xe B quay theo chiều nào?
.png)
BÀI GIẢI
• Khi bánh xe A quay theo chiều dương, bánh xe B quay theo chiều âm.
3. Trên một chiếc đồng hồ từ lúc 12 giờ đến 15 giờ, kim giờ và kim phút đã quay một góc bao nhiêu độ?
.png)
BÀI GIẢI
• Kim giờ quay một góc 90°, còn kim phút quay một góc -3.360° = -1080°.
4. Cho tam giác ABC và điểm O. Dựng ảnh của tam giác đó qua phép quay tâm O góc 60°.
BÀI GIẢI
• Ta dựng được ảnh của tam giác ABC qua $Q_{(O,60^{0})}$
.png)
III.GIẢI BÀI TẬP SÁCH GIÁO KHOA:
1. Cho hình vuông ABCD tâm O (h.1.38).
a) Tìm ảnh của điểm C qua phép quay tâm A góc 90°.
b) Tìm ảnh của đường thẳng BC qua phép quay tâm O góc 90°.
.png)
BÀI GIẢI
a) Gọi E = $Q_{(A,90^{0})}$ (C) thì AE = AC và góc CAE = 90° nên $\Delta$AEC vuông cân đỉnh A, có đường cao AD. Do đó D là trung điểm của EC.
b) Ta có: $Q_{(O,90^{0})}$ (B) = C và $Q_{(O,90^{0})}$ (C) = D.
Do đó $Q_{(O,90^{0})}$ (BC) = CD.
.png)
2. Trong mặt phẳng tọa độ Oxy cho điểm A(2; 0) và đường thẳng d có phương trình x + y - 2 = 0. Tìm ảnh của A và d qua phép quay tâm O góc 90°.
BÀI GIẢI
• Ta có: A(2; 0) thuộc tiaOx.
- Gọi $Q_{(O,90^{0})}$ (A) = B thì B thuộc tia Oy và OA = OB nên B(0; 2).
• Ta thấy tọa độ A, B đều thỏa phương trình x + y - 2 = 0 của đường thẳng d nên A, B thuộc d.
- Do $Q_{(O,90^{0})}$ (A) = B và $Q_{(O,90^{0})}$ (B) = C(-2; 0) nên ảnh của d chính là đường thẳng BC có phương trình theo đoạn chắn là:
$\large \frac{x}{x_{C}}+\frac{y}{y_{B}}=1$ ⇔ $\large \frac{x}{-2}+\frac{y}{2}=1$ hay y - x - 2 = 0
.png)
