§4. HAI MẶT PHẲNG VUÔNG GÓC
I. TÓM TẮT LÝ THUYẾT:
1. Góc giữa hai mặt phẳng:
a) Định nghĩa:
• Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
• Nếu hai mặt phẳng song song hoặc trùng nhau thì ta nói rằng góc giữa hai mặt phẳng đó bằng 0°.
.png)
b) Cách xác định góc giữa hai mặt phẳng:
• Giả sử hai mặt phẳng ($\alpha$) và ($\beta$) cắt nhau theo giao tuyến c. Từ một điểm I bất kì trên c ta dựng trong ($\alpha$) đường thẳng a vuông góc với c và dựng trong ($\beta$) đường thẳng b vuông góc với c.
• Người ta chứng minh được góc giữa hai mặt phẳng ($\alpha$) và ($\beta$) là góc giữa hai đường thẳng a và b.
.png)
Diện tích hình chiếu của một đa giác:
• Cho đa giác H nằm trong mp($\alpha$) và có diện tích S, H' là hình chiếu vuông góc của H trên mp($\beta$).
• Diện tích S' của H' được tính bởi công thức S' = S.cos$\varphi$ (trong đó $\varphi$ là góc giữa ($\alpha$) và ($\beta$)).
.png)
2. Hai mặt phẳng vuông góc:
a) Định nghĩa:
• Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là góc vuông.
• Nếu hai mặt phẳng ($\alpha$) và ($\beta$) vuông góc nhau, ta kí hiệu ($\alpha$) $\perp$ ($\beta$).
.png)
b) Các định lí:
Định lí 1:
Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia:
($\alpha$) $\perp$ ($\beta$) ⇔ $\exists$a $\subset$ ($\alpha$): a $\perp$ ($\beta$).
Hệ quả 1:
Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.
.png)
Hệ quả 2:
Cho hai mặt phẳng ($\alpha$) và ($\beta$) vuông góc với nhau. Nếu từ một điểm thuộc mặt phẳng ($\alpha$) ta dựng đường thẳng vuông góc với mặt phẳng ($\beta$) thì đường thẳng này nằm trong mặt phẳng ($\alpha$).
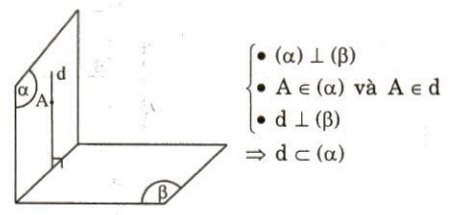
Định lí 2:
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thì giao tuyến của chúng vuông góc với mặt phẳng đó.
.png)
3. Hình lăng trụ đứng:
.png)
.png)
4. Hình chóp đều và hình chóp cụt đều:
a) Hình chóp đều:
• Định nghĩa:
Một hình chóp gọi là hình chóp đều nếu đáy của nó là đa giác đều và các cạnh bên bằng nhau.
.png)
Đường vuông góc kẻ từ đỉnh hình chóp đến mặt đáy gọi là đường cao của hình chóp.
* Hình chóp là hình chóp đều khi và chỉ khi đáy của nó là đa giác đều và chân đường cao của hình chóp trùng với tâm của đáy (tâm của đa giác đều chính là tâm đường tròn ngoại tiếp và nội tiếp đa giác đó).
* Hình chóp là hình chóp đều khi và chỉ khi đáy của nó là đa giác đều và các cạnh bên tạo với mặt đáy các góc bằng nhau.
• Hệ quả:
Các mặt bên của hình chóp đều là các tam giác cân bằng nhau.
b) Hình chóp cụt đều:
.png)
• Định nghĩa:
- Phần của hình chóp đều nằm giữa đáy và một thiết diện song song với đáy cắt tất cả các cạnh bên của hình chóp đều gọi là hình chóp cụt đều.
- Cho hình chóp đều $S.A_{1}A_{2}...A_{n}$. Một phần mặt phẳng (P) song song với mặt phẳng đáy $A_{1}A_{2}...A_{n}$ cắt các cạnh bên $SA_{1}$, $SA_{2}$, ..., $SA_{n}$ lần lượt tại $A'_{1}$, $A'_{2}$, ..., $A'_{n}$.
* Phần hình chóp đều $S.A_{1}A_{2}...A_{n}$ nằm giữa đáy $A_{1}A_{2}...A_{n}$ và (P) gọi là hình chóp cụt đều.
* Đa giác $A_{1}A_{2}...A_{n}$ và thiết diện $A'_{1}$, $A'_{2}$, ..., $A'_{n}$ gọi là hai đáy của hình chóp cụt đều; các hình $A_{1}A'_{1}A'_{2}A_{2}$, $A_{2}A'_{2}A'_{3}A_{3}$, ..., $A_{n}A'_{n}A'_{1}A_{1}$ gọi là các mặt bên của hình chóp cụt đều. Đoạn nối hai tâm O và O' của hai đáy gọi là đường cao của hình chóp cụt đều.
Nhận xét:
- Các mặt cạnh bên của hình chóp cụt đều có độ dài bằng nhau.
- Các mặt cạnh bên của hình chóp cụt đều là các hình thang cân bằng nhau.
III.GIẢI ĐÁP CÂU HỎI SÁCH GIÁO KHOA:
1. Cho hai mặt phẳng ($\alpha$) và ($\beta$) vuông góc với nhau và cắt nhau theo giao tuyến d. Chứng minh rằng nếu có một đường thẳng $\Delta$ nằm trong ($\alpha$) và $\Delta$ vuông góc với d thì $\Delta$ vuông góc với ($\beta$).
BÀI GIẢI
.png)
• Từ một điểm O thuộc d, trong mp ($\alpha$). Vẽ đường thẳng $\Delta$ vuông góc với d và trong ($\beta$) vẽ đường thẳng $\Delta$' vuông góc với d.
Ta có góc giữa hai đường thẳng $\Delta$ và $\Delta$' là góc giữa hai mặt phẳng ($\alpha$) và ($\beta$). Vì ($\alpha$) vuông góc với ($\beta$) nên góc giữa hai đường thẳng $\Delta$ và $\Delta$' bằng 90°, nghĩa là $\Delta$ vuông góc với $\Delta$'. Mặt khác theo cách dựng ta có $\Delta$ vuông góc với d. Do đó $\Delta$ vuông góc với mp(d, $\Delta$') hay $\Delta$ vuông góc với ($\beta$).
2. Cho tứ diện ABCD có ba cạnh AB, AC, AD đôi một vuông góc với nhau. Chứng minh rằng các mặt phẳng (ABC), (ACD), (ADB) từng đôi một vuông góc với nhau.
BÀI GIẢI
.png)
* Chứng minh (ABC) $\perp$ (ACD).
.png)
Mà AB $\subset$ (ABC) ⇒ (ABC) $\perp$ (ACD)
* Chứng minh tương tự (ABC) $\perp$ (ADB), (ACD) $\perp$ (ADB).
3. Cho hình vuông ABCD. Dựng đoạn thẳng AS vuông góc với mặt phẳng chứa hình vuông ABCD.
a) Hãy nêu tên các mặt phẳng lần lượt chứa các đường thẳng SB, SC, SD và vuông góc với mặt phẳng (ABCD).
b) Chứng minh rằng mặt phẳng (SAC) vuông góc với mặt phẳng (SBD).
BÀI GIẢI
.png)
a) Các mặt phẳng lần lượt chứa SB, SC, SD đều phải chứa SA vì SA vuông góc với mp (ABCD) và khi đó các mp(SA, SB), (SA, SC) và (SA, SD) đều vuông góc với mp(ABCD).
b) Chứng minh (SAC) $\perp$ (SBD).
.png)
• Mặt khác BD $\perp$ AC (vì ABCD là hình vuông)
.png)
Mà BD $\subset$ (SBD) ⇒ (SAC) $\perp$ (SBD) (đpcm).
4. Cho biết mệnh để nào sau đây là đúng?
a) Hình hộp là hình lăng trụ đứng.
b) Hình hộp chữ nhật là hình lăng trụ đứng.
c) Hình lăng trụ là hình hộp.
d) Có hình lăng trụ không phải là hình hộp.
BÀI GIẢI
a) Sai;
b) Đúng;
c) Sai;
d) Đúng.
5. Sáu mặt của hình hộp chữ nhật có phải là những hình chữ nhật không?
BÀI GIẢI
• Sáu mặt của hình hộp chữ nhật đều là những hình chữ nhật.
6. Chứng minh rằng hình chóp đều có các mặt bên là những tam giác cân bằng nhau
BÀI GIẢI
Vì hình chóp đều có đáy là một đa giác đều và chân đường cao trùng với tâm của đa giác đáy nên ta suy ra hình chóp đều có các cạnh bên bằng nhau. Do đó các mặt bên của một hình chóp đều là những tam giác cân bằng nhau.
7. Có tồn tại một hình chóp tứ giác S.ABCD có hai mặt bên (SAB) và (SCD) cùng vuông góc với mặt phẳng đáy hay không?
BÀI GIẢI
.png)
Trong mặt phẳng ($\alpha$) ta lấy tứ giác ABCD có hai cạnh AB và CD cắt nhau tại O.
Trên đường thẳng A vuông góc với ($\alpha$) tại O lấy một điểm S ngoài ($\alpha$) và lập nên hình chóp S.ABCD. Hai mặt bên (SAB) và (SCD) đều vuông góc với mặt phẳng đáy vì chúng đều chứa đường thẳng SO vuông góc với mặt phẳng ($\alpha$).
III. GIẢI BÀI TẬP SÁCH GIÁO KHOA:
1. Cho ba mặt phẳng ($\alpha$), ($\beta$), ($\gamma$), mệnh đề nào sau đây đúng?
a) Nếu ($\alpha$) $\perp$ ($\beta$) và ($\alpha$) // ($\gamma$) thì ($\beta$) $\perp$ ($\gamma$).
b) Nếu ($\alpha$) $\perp$ ($\beta$) và ($\alpha$) $\perp$ ($\gamma$) thì ($\beta$) // ($\gamma$).
BÀI GIẢI
a) Đúng vì:
Lấy M $\in$ ($\beta$), vẽ đường thẳng a qua M và vuông góc với ($\alpha$)
Ta có:
• a $\subset$ ($\beta$) (1) vì ($\beta$) $\perp$ ($\alpha$)
• a $\perp$ ($\gamma$) (2) vì ($\gamma$) // ($\alpha$)
Từ (1) và (2) ⇒ ($\beta$) $\perp$ ($\gamma$).
.png)
b) Sai vì, chẳng hạn hai mặt phẳng ($\beta$) và ($\gamma$) cùng đi qua đường thẳng a và a $\perp$ ($\alpha$), ta có:
• ($\beta$) $\supset$ a mà a $\perp$ ($\alpha$) ⇒ ($\beta$) $\perp$ ($\alpha$)
• ($\gamma$) $\supset$ a mà a $\perp$ ($\alpha$) ⇒ ($\gamma$) $\perp$ ($\alpha$)
Vậy ($\beta$) và ($\gamma$) là hai mặt phẳng cùng vuông góc với ($\alpha$).
.png)
2. Cho hai mặt phẳng ($\alpha$) và ($\beta$) vuông góc với nhau. Người ta lấy trên giao tuyến của hai mặt phẳng đó hai điểm A và B sao cho AB = 8cm. Gọi C là một điểm trên ($\alpha$) và D là một điểm trên ($\beta$) sao cho AC và BD cùng vuông góc với giao tuyến $\Delta$ và AC = 6cm, BD = 24cm. Tính độ dài đoạn CD.
BÀI GIẢI
.png)
Nối AD, CD ta có:
• DB $\perp$ ($\Delta$) nên $\Delta$ABD vuông cho ta: $AD^{2}$ = $AB^{2}$ + $BD^{2}$
• ($\alpha$) $\perp$ ($\beta$) theo giao tuyến $\Delta$
AC $\subset$ ($\beta$) và AC $\perp$ $\Delta$
⇒ AC $\perp$ ($\beta$).
Vậy AC $\perp$ AD nên $\Delta$ACD vuông cho ta:
$CD^{2}$ = $AC^{2}$ + $AD^{2}$
= $AC^{2}$ + ($AB^{2}$ + $BD^{2}$) = $6^{2}$ + $8^{2}$ + $24^{2}$ = 676.
Vậy CD = 26 (cm).
3. Trong mặt phẳng ($\alpha$) cho tam giác ABC vuông ở B. Một đoạn thẳng AD vuông góc với ($\alpha$) tại A. Chứng minh rằng:
a) $\widehat{ABD}$ là góc giữa hai mặt phẳng (ABC) và (DBC);
b) Mặt phẳng (ABD) vuông góc với mặt phẳng (BCD);
c) HK // BC với H và K lần lượt là giao điểm của DB và DC với mặt phẳng (P) đi qua A và vuông góc với DB.
BÀI GIẢI
.png)
a) Chứng minh $\widehat{ABD}$ là góc giữa hai mặt phẳng (ABC) và (DBC).
• Ta có: AD $\perp$ (ABC) ⇒ AD $\perp$ BC,
mà BC $\perp$ AB nên BC $\perp$ (ABD) ⇒ BC $\perp$ BD
Ta có: $\left\{\begin{matrix} AB\perp BC\\ BD\perp BC \end{matrix}\right.$
⇒ $\widehat{ABD}$ là góc giữa hai mặt phẳng (ABC) và (DBC).
b) Chứng minh (ABD) $\perp$ (BCD).
.png)
c) Chứng minh HK // BC.
.png)
4. Cho hai mặt phẳng ($\alpha$), ($\beta$) cắt nhau và một điểm M không thuộc ($\alpha$) và không thuộc ($\beta$). Chứng minh rằng qua điểm M có một và chỉ một mặt phẳng (P) vuông góc với ($\alpha$) và ($\beta$). Nếu ($\alpha$) song song ($\beta$) thì kết quả trên sẽ thay đổi như thế nào?
BÀI GIẢI
• Trường hợp ($\alpha$) cắt ($\beta$):
.png)
Gọi a là giao tuyến của ($\alpha$), ($\beta$) và (P) là mp qua M, ta có:
.png)
Vậy (P) là mặt phẳng đi qua điểm M và vuông góc với đường thẳng a, nên (P) duy nhất.
• Trường hợp ($\alpha$) // ($\beta$):
.png)
Qua M, vẽ đường thẳng a $\perp$ ($\alpha$), lúc đó a $\perp$ ($\beta$)
mp (R) qua a ⇒ (R) $\perp$ ($\alpha$) và (R) $\perp$ ($\beta$)
Vì có vô số mặt phẳng (R) qua a nên có vô số mặt phẳng qua M và vuông góc với ($\alpha$) và ($\beta$).
5. Cho hình lập phương ABCD.A'B'C'D'. Chứng minh rằng:
a) Mặt phẳng (AB'C'D) vuông góc với mặt phẳng (BCD'A');
b) Đường thẳng AC' vuông góc với mặt phẳng (A'BD).
BÀI GIẢI
.png)
a) Chứng minh (AB'C'D) $\perp$ (BCD'A').
• Ta có AB' $\perp$ BA' (đường chéo hình vuông)
$\left\{\begin{matrix} BC\perp AB\\ BC\perp BB' \end{matrix}\right.$ ⇒ BC $\perp$ (ABB'A') ⇒ BC $\perp$ AB'
• Vậy $\left\{\begin{matrix} AB'\perp BA'\\ AB'\perp BC \end{matrix}\right.$
⇒ AB' $\perp$ (BCD'A')
mà AB' $\subset$ (AB'C'D')
⇒ (AB'C'D) $\perp$ (BCD'A').
b) Chứng minh AC' $\perp$ (A'BD).
• Ta có:
.png)
⇒ A'B $\perp$ AC'.
.png)
⇒ BD $\perp$ AC'. (2)
Từ (1) và (2) ⇒ AC' $\perp$ (A'BD) (đpcm).
6. Cho hình chóp S.ABCD có đáy ABCD là một hình thoi cạnh a và có SA = SB = SC = a. Chứng minh rằng:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Tam giác SBD là tam giác vuông.
BÀI GIẢI
.png)
a) Chứng minh (ABCD) $\perp$ (SBD).
Gọi O = AC $\cap$ BD. Ta có:
SO $\perp$ AC (SO là đường trung tuyến tam giác cân (SAC)
BD $\perp$ AC (ABCD là hình thoi)
SO, BD cắt nhau trong (SBD)
⇒ AC $\perp$ (SBD)
mà AC $\subset$ (ABCD)
⇒ (ABCD) $\perp$ (SBD)
b) Chứng minh tam giác SBD là tam giác vuông cân:
Xét ba tam giác SAC, BAC và DAC, ta có:
SA = SC = BA = BC = DA = DC = a (giả thiết)
Chung cạnh AC
⇒ Ba tam giác SAC, BAC và DAC là ba tam giác cân bằng nhau (chung cạnh đáy AC).
⇒ SO = BO = DO.
⇒ Tam giác SBD vuông ở S (đpcm).
7. Cho hình hộp chữ nhật ABCD. A'B'C'D' có AB = a, BC = b, CC' = c.
a) Chứng minh rằng mặt phẳng (ADC'B') vuông góc với mặt phẳng (ABB'A').
b) Tính độ dài đường chéo AC' theo a, b, c.
BÀI GIẢI
.png)
a) Chứng minh (ADC'B') $\perp$ (ABB'A')
Hình hộp chữ nhật là hình lăng trụ đứng.
Nên cạnh bên AA' $\perp$ (ABCD) ⇒ AA' $\perp$ AD
Và đáy ABCD là hình chữ nhật ⇒ AB $\perp$ AD
Vậy: $\left\{\begin{matrix} AD\perp (ABB'A')\\ AD\subset (ADC'B') \end{matrix}\right.$ ⇒ (ADC'B') $\perp$ (ABB'A') (đpcm)
b) Tính AC'.
Cạnh bên CC' $\perp$ đáy (ABCD) ⇒ CC' $\perp$ AC.
Tam giác vuông ACC', ta có: $AC'^{2}$ = $CC'^{2}$ + $AC^{2}$
Tam giác vuông ABC, ta có: $AC^{2}$ = $AB^{2}$ + $BC^{2}$
⇒ $AC'^{2}$ = $CC'^{2}$ + $AB^{2}$ + $BC^{2}$ = $a^{2}$ + $b^{2}$ + $c^{2}$
Vậy AC' = $\sqrt{a^{2}+b^{2}+c^{2}}$.
8. Tính độ dài đường chéo của một hình lập phương cạnh a.
BÀI GIẢI
.png)
• Ta có:
B'C' $\perp$ A'B' (A'B'C'D' là hình vuông)
B'C' $\perp$ BB' (BCC'B' là hình vuông)
A'B', BB' cắt nhau trong mp(ABB'A')
⇒ B'C' $\perp$ mp(ABB'A')
• Mà AB' $\subset$ (ABB'A') ⇒ B'C' $\perp$ AB'.
• Trong tam giác vuông AB'C', ta có: $AC'^{2}$ = $AB'^{2}$ + $B'C'^{2}$
• Trong tam giác vuông AA'B', ta lại có: $AB'^{2}$ = $AA'^{2}$ + $A'B^{2}$
⇒ $AC'^{2}$ = $AA'^{2}$ + $A'B^{2}$ + $B'C'^{2}$
⇒ $AC'^{2}$ = $a^{2}$ + $a^{2}$ + $a^{2}$
⇒ AC' = $\sqrt{a^{2}+a^{2}+a^{2}}$ = $\sqrt{3a^{2}}$.
Vậy AC' = $a\sqrt{3}$.
9. Cho hình chóp tam giác đều S.ABC có SH là đường cao. Chứng minh SA $\perp$ BC và SB $\perp$ AC.
BÀI GIẢI
.png)
* Chứng minh SA $\perp$ BC.
Vì H là tâm của tam giác đều nên ta có:
• BC $\perp$ AH và BC $\perp$ SH.
Ta có: $\left\{\begin{matrix} BC\perp AH\\ BC\perp SH \end{matrix}\right.$ ⇒ BC $\perp$ (SAH) ⇒ BC $\perp$ SA
* Chứng minh SB $\perp$ AC.
Ta có: $\left\{\begin{matrix} AC\perp BH\\ AC\perp SH \end{matrix}\right.$ ⇒ AC $\perp$ (SBH) ⇒ AC $\perp$ SB
10. Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.
a) Tính độ dài đoạn thẳng SO.
b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau.
c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD).
BÀI GIẢI
.png)
a) Tính độ dài đoạn thẳng SO.
• Xét tam giác SAC, ta có: SA = SC, O là trung điểm của AC ⇒ SO $\perp$ AC.
• Xét tam giác SBD, ta có: SB = SD, O là trung điểm của BD ⇒ SO $\perp$ BD.
• Khi đó:
SO $\perp$ AC
SO $\perp$ BD
AC cắt BD trong mp (ABCD)
⇒ SO $\perp$ (ABCD)
.png)
b) Chứng minh (MBD) $\perp$ (SAC).
$\Delta$SBC, $\Delta$SDC là tam giác đều có cạnh bằng a, M là trung điểm SC
⇒ $\left\{\begin{matrix} SC\perp BM\\ SC\perp DM \end{matrix}\right.$ ⇒ SC $\perp$ (MBD)
Mà SC $\subset$ (SAC) nên (SAC) $\perp$ (MBD).
c) Tính OM. Góc giữa (MBD) và (ABCD).
• Tính độ dài OM.
• Ta có:
SO $\perp$ OC (vì SO $\perp$ (ABCD))
SO = OC = $\large \frac{a\sqrt{2}}{2}$
⇒ Tam giác SOC vuông cân ở O và có cạnh huyền SC = a
⇒ OM = $\large \frac{SC}{2}$ = $\large \frac{a}{2}$
• Góc giữa hai mặt phẳng (MBD) và (ABCD)
(MBD) $\cap$ (ABCD)= BD
OC $\subset$ (ABCD) và OC $\perp$ BD
OM $\subset$ (MBD) và OM $\perp$ BD
⇒ $\widehat{MOC}$ là góc giữa hai mặt phẳng (MBD) và (ABCD).
• Ta lại có : OM = MC = $\large \frac{a}{2}$
• OM $\perp$ SC (vì tam giác SOC vuông cân ở O và M là trung điểm SC).
⇒ Tam giác OMC vuông cân ở M ⇒ $\widehat{MOC}$ = 45°.
• Vậy góc giữa hai mặt phẳng (MBD) và (ABCD) bằng 45°.
11. Cho hình chóp S.ABCD có đáy ABCD là một hình thoi tâm I cạnh a và có góc A bằng 60°, cạnh SC = $\large \frac{a\sqrt{6}}{2}$ và SC vuông góc với mặt phẳng (ABCD).
a) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC).
b) Trong tam giác SCA kẻ IK vuông góc với SA tại K. Hãy tính độ dài IK.
c) Chứng minh $\widehat{BKD}$ = 90° từ đó suy ra mặt phẳng (SAB) vuông góc với mặt phẳng (SAD).
BÀI GIẢI
.png)
a) Chứng minh (SBD) $\perp$ (SAC).
• Vì ABCD là hình thoi nên:
BD $\perp$ AC (1)
$\left\{\begin{matrix} SC\perp (ABCD)\\ BD\subset (ABCD) \end{matrix}\right.$ ⇒ BD $\perp$ SC (2)
• Từ (1) và (2) suy ra BD $\perp$ (SAC)
Mà BD $\subset$ (SBD)
• Vậy (SBD) $\perp$ (SAC) (đpcm).
b) Tính độ dài IK.
• Ta có AB = AD = a ⇒ $\Delta$ABD cân tại A.
• Ta lại có $\widehat{A}$ = 60° ⇒ $\Delta$ABD đều ⇒ AB = AD = BC = a.
• Vì I là trung điểm của BD do đó AI vừa là trung tuyến vừa là đường cao nên:
⇒ AI $\perp$ BD; BI = $\large \frac{BD}{2}$ = $\large \frac{a}{2}$
• Hay $\Delta$AIB vuông tại I, cho ta: $AB^{2}$ = $AI^{2}$ + $BI^{2}$
.png)
• Mà AC = 2AI ⇒ AC = 2. $\large \frac{a\sqrt{3}}{2}$ = a$\sqrt{3}$.
• Vì SC $\perp$ (ABCD) ⇒ SC $\perp$ AC.
Xét $\Delta$SAC vuông tại C, ta có:
.png)
⇒ SA = $\large \frac{3a\sqrt{2}}{2}$
• Hai tam giác AKI và ACS đồng dạng nên: $\large \frac{IK}{SC}$ = $\large \frac{AI}{SA}$
.png)
c) Chứng minh $\widehat{BKD}$ = 90°.
• Do BD $\perp$ (SAC) ⇒ SA $\perp$ BD.
$\left\{\begin{matrix} SA\perp IK\\ SA\perp BD \end{matrix}\right.$ ⇒ SA $\perp$ (BKD) ⇒ BK $\perp$ SA
• Và DK $\perp$ SA ⇒ $\widehat{DKB}$ là góc giữa hai mặt phẳng (SAB) và (SAD).
• Tam giác ABD là tam giác đều nên BD = a. Vì BD = a; IK = $\large \frac{a}{2}$
⇒ IK = $\large \frac{BD}{2}$
• Tam giác BIK có trung tuyến IK bằng $\large \frac{1}{2}$ cạnh tương ứng nên BIK là tam giác vuông
⇒ $\widehat{BIK}$ = 90°.
• Suy ra góc giữa hai mp (SAB) và (SAD) bằng 90°. Vậy (SAB) $\perp$ (SAD).
