VẤN ĐỀ 3. CẤP SỐ CỘNG
A. Kiến thức cần nhớ
Định nghĩa
Cấp số cộng là một dãy số (hữu hạn hay vô hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số hạng đứng ngay trước nó và một số d không đổi. Nghĩa là:
($u_{n}$) là cấp số cộng ⇔ $\forall$ n $\geq$ 2, $u_{n}$ = $u_{n-1}$ + d.
Số d được gọi là công sai của cấp số cộng.
Định lí 1
Nếu ($u_{n}$) là một cấp số cộng thì kể từ số hạng thứ hai, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng hữu hạn) đều là trung bình cộng của hai số hạng đứng kề nó trong dãy, tức là
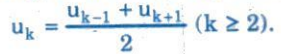
Định lí 2
Nếu một cấp số cộng có số hạng đầu $u_{1}$ và công sai d thì số hạng tổng quát $u_{n}$ của nó được xác định bởi công thức
$u_{n}$ = $u_{1}$ + (n - 1)d.
Định lí 3
Giả sử ($u_{n}$) là một cấp số cộng. Với mỗi số nguyên dương n, gọi $S_{n}$ tổng n số hạng đầu tiên của nó ($S_{n}$ = $u_{1}$ + $u_{2}$ + ... + $u_{n}$).
Khi đó, ta có
.png)
với mọi n $\geq$ 1.
B. Giải bài tập sách giáo khoa
Bài 1
Trong các dãy số ($u_{n}$) sau đây, dãy nào là cấp số cộng? Tính số hạng đầu và công sai của nó.
a) $u_{n}$ = 5 - 2n
b) $u_{n}$ = $\large \frac{n}{2}$ - 1
c) $u_{n}$ = $3^{n}$
d) $u_{n}$ = $\large \frac{7-3n}{2}$
Giải
Phương pháp chung là xét hiệu H = $u_{n+1}$ - $u_{n}$.
Nếu H là hằng số thì dãy số là cấp số cộng.
Nếu H = f(n) thì dãy số không phải là cấp số cộng.
a) $u_{n+1}$ - $u_{n}$ = -2, vậy dãy số là cấp số cộng có $u_{1}$ = 3 và d = -2.
b) Dãy số là cấp số cộng với u = - $\large \frac{1}{2}$ và d = $\large \frac{1}{2}$
c) $u_{n+1}$ - $u_{n}$ = 2.$3^{n}$, vậy dãy số không phải là cấp số cộng.
d) Dãy số là cấp số cộng có $u_{1}$ = 2, d = -$\large \frac{3}{2}$
Bài 2
Tìm số hạng đầu và công sai của các cấp số cộng sau, biết:
.png)
.png)
Giải
Sử dụng công thức $u_{n}$ = $u_{1}$ + (n - 1)d.
a) Giải hệ
.png)
Đáp số: $u_{1}$ = 16, d = -3
b) Giải hệ
.png)
Đáp số: $u_{1}$ = 3 và d = 2 hoặc $u_{1}$ = -17 và d = 2.
Bài 3
Trong các bài toán về cấp số cộng, ta thường gặp năm đại lượng $u_{1}$, d, n, $u_{n}$, $S_{n}$
a) Hãy viết các hệ thức liên hệ giữa các đại lượng đó. Cần phải biết ít nhất mấy đại lượng để có thể tìm được các đại lượng còn lại?
b) Lập bảng theo mẫu sau và điền số thích hợp vào ô trống:
| $u_{1}$ | d | $u_{n}$ | n | $S_{n}$ |
| -2 | 55 | 20 | ||
| -4 | 15 | 120 | ||
| 3 | $\large \frac{4}{27}$ | 7 | ||
| 17 | 12 | 72 | ||
| 2 | -5 | -205 |
Giải
a) Cần biết ít nhất ba trong năm đại lượng $u_{1}$, d, n, $u_{n}$, $S_{n}$ thì có thể tính được hai đại lượng còn lại.
b) Thực chất đây là năm bài tập nhỏ ứng với các dữ liệu ở năm dòng.
Học sinh phải giải từng bài nhỏ rồi mới điền kết quả.
b1) Biết $u_{1}$ = -2, $u_{n}$ = 55, n = 20. Tìm d, $S_{n}$
Đáp số: d = 3, $S_{20}$ = 530
b2) Biết d = -4, n = 15, $S_{n}$ = 120. Tìm $u_{1}$, $u_{n}$
Áp dụng các công thức $u_{n}$ và .png) , ta có:
, ta có: .png)
Giải hệ trên, ta được $u_{1}$ = 36, $u_{15}$ = -20.
Tuy nhiên, nếu sử dụng công thức
.png)
Ta có ngay $u_{1}$ = 36 và tìm tiếp $u_{15}$ = -20.
Cách giải này gọn hơn do việc lựa chọn công thức $S_{n}$ phù hợp với việc biết n và d.
b3) Đáp số: n = 28, $S_{n}$ = 140
b4) Đáp số: $u_{1}$ = -5, d = 2
b5) Đáp số: n = 10, $u_{n}$ = -43
Bài 4
Mặt sàn tầng một của một ngôi nhà cao hơn mặt sân 0,5m. Cầu thang đi từ tầng một lên tầng hai gồm 21 bậc, mỗi bậc cao 18cm.
a) Viết công thức để tìm độ cao của một bậc tùy ý so với mặt sân.
b) Tính độ cao của sàn tầng hai so với mặt sân.
Giải
a) Gọi chiều cao của bậc thứ n so với mặt sân là $h_{n}$ ta có:
$h_{n}$ = 0,5 + n.0,18
b) Chiều cao mặt sàn tầng hai so với mặt sân là
$h_{21}$ = 0,5 + 21.0,18 = 4,28 (m).
Bài 5
Từ 0 giờ đến 12 giờ trưa, đồng hồ đánh bao nhiêu tiếng, nếu nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ?
Giải
Tính tổng 1 + 2 + 3 + ... + 12 = 78.
C. Bài tập bổ sung
Bài 1
Chứng minh rằng mỗi dãy số sau là một cấp số cộng và hãy xác định công sai của mỗi cấp số cộng đó:
a) Dãy số ($u_{n}$) với $u_{n}$ = 19n - 5.
b) Dãy số ($u_{n}$) với $u_{n}$ = an + b, trong đó a và b là các hằng số.
Do đó ($u_{n}$) là một cấp số cộng với công sai d = 19.
b) Ta có $u_{n+1}$ - $u_{n}$ = a(n + 1) + b - (an + b) = a $\forall$ n $\geq$ 1.
Do đó ($u_{n}$) là một cấp số cộng với công sai d = a.
Bài 2
Một cấp số cộng có năm số hạng mà tổng của số hạng đầu và số hạng thứ ba bằng 28, tổng của số hạng thứ ba và số hạng cuối bằng 40. Hãy tìm cấp số cộng đó.
Giải
Với mỗi n $\in$ {1, 2, 3, 4, 5}, kí hiệu $u_{n}$ là số hạng thứ n của cấp số cộng đã cho. Ta có:
28 = $u_{1}$ + $u_{3}$ = 2$u_{2}$ ⇒ $u_{2}$ = 14
40 = $u_{3}$ + $u_{5}$ = 2$u_{4}$ ⇒ $u_{4}$ = 20
2$u_{3}$ = $u_{2}$ + $u_{4}$ = 34 ⇒ $u_{3}$ = 17
Từ đó $u_{1}$ = 28 - $u_{3}$ = 11 và $u_{5}$ = 40 - $u_{3}$ = 23
Vậy, cấp số cộng cần tìm là: 11, 14, 17, 20, 23.
Bài 3
Hãy tìm số hạng tổng quát của cấp số cộng ($u_{n}$), biết rằng $u_{23}$ - $u_{17}$ = 30 và $(u_{17})^{2}$ + $(u_{23})^{2}$ = 450.
Giải
Gọi d là công sai của cấp số cộng đã cho. Ta có
.png)
Bài 4
Cho cấp số cộng ($u_{n}$) có $u_{2}$ + $u_{22}$ = 60. Hãy tính tổng 23 số hạng đầu tiên của cấp số đó.
Giải
Gọi d là công sai của cấp số cộng đã cho, ta có
$u_{1}$ = $u_{2}$ - d và $u_{23}$ = $u_{22}$ + d.
Do đó, áp dụng Định lí 3 cho n = 23, ta được
.png)
Bài 5
Số đo ba góc của một tam giác vuông lập thành một cấp số cộng. Hãy tìm số đo ba góc đó.
Giải
Kí hiệu A, B, C là số đo ba góc (tính theo đơn vị độ) của tam giác vuông đã cho. Không mất tính tổng quát, có thể giả sử A $\leq$ B $\leq$ C. Khi đó, từ giả thiết dễ dàng suy ra C = 90 (độ) và A, B, C theo thứ tự đó là một cấp số cộng. Gọi d là công sai của cấp số cộng đó, ta có
A = C - 2d và B = C - d
Suy ra 90 = A + B = 2C - 3d = 180 - 3d. Do đó d = 30.
Vì thế A = 90 - 2.30 (độ) và B = 90 - 30 = 60 (độ).
Bài 6
Cho hai cấp số cộng
5, 8, 11,... và 3, 7, 11,...
Hỏi trong 100 số hạng đầu tiên ở mỗi cấp số, có bao nhiêu số hạng chung?
Giải
Giả sử $u_{n}$ là số hạng của cấp số cộng thứ nhất và $u_{m}$ là số hạng bằng nó ở cấp số cộng thứ hai, nghĩa là
5 + (n - 1).3 = 3 + (m - 1)4
hay 3n + 2 = 4m – 1. Từ đó có n = $\large \frac{m}{3}$ + m – 1
Đặt $\large \frac{m}{3}$ = t thì m = 3t và n = 4t – 1.
Để m và n thuộc N*, ta phải có t $\in$ N*. Ngoài ra vì m, n không lớn hơn 100.
nên .png)
Suy ra 1 $\leq$ t $\leq$ 25, tức là t = 1, 2, 3, 4,..., 25.
Tương ứng với 25 giá trị của t, ta được dãy các số hạng chung cần tìm gồm 25 số hạng, đó là 11, 23, 35,..., 299.
D. Bài tập đề nghị
Bài 1
Cho dãy số ($u_{n}$) với $u_{n}$ = 9 - 5n.
a) Viết 5 số hạng đầu của dãy.
b) Chứng minh dãy số ($u_{n}$) là cấp số cộng. Chỉ rõ $u_{1}$ và d.
c) Tính tổng của 100 số hạng đầu.
Bài 2
a) Viết 6 số xen giữa hai số 3 và 24 để được một cấp số cộng có 8 số hạng. Tính tổng các số hạng của cấp số này.
b) Viết 5 số hạng xen giữa hai số 25 và 1 để được một cấp số cộng có 7 số hạng. Số hạng thứ 50 của cấp số này là bao nhiêu?
Bài 3
Cho hai cấp số cộng
.png)
Hỏi trong 100 số hạng đầu tiên của mỗi cấp số có bao nhiêu số hạng chung?
Bài 4
Tìm x, biết các cấp số cộng .png) và
và
a) 1 + 6 + 11 + 16 + ... + x = 970
b) (x + 1) + (x + 4) + ... + (x + 28) = 155
Bài 5
Chứng minh rằng ba số dương a, b, c lập thành một cấp số cộng khi và chỉ khi các số .png) lập thành một cấp số cộng.
lập thành một cấp số cộng.
Bài 6
Chu vi của một đa giác 158cm, số đo các cạnh của nó lập thành một cấp số cộng với công sai d = 3cm. Biết cạnh lớn nhất là 44cm, tính số cạnh của đa giác đó.
Bài 7
Có thể có một tam giác mà số đo các cạnh và chu vi của nó lập thành một cấp số cộng được không?
Bài 8
.png)
