§1. KHÁI NIỆM VỀ KHỐI ĐA DIỆN
B. CÂU HỎI VÀ BÀI TẬP
Bài 1. Chứng minh rằng nếu khối đa diện có các mặt là tam giác thì số mặt phải là số chẵn. Hãy chỉ ra những khối đa diện như thế với số mặt bằng 4, 6, 8, 10.
Giải
Gọi C là số cạnh và M là số mặt.
Vì mỗi mặt là tam giác và có M mặt, nên số cạnh là 3M. Nhưng mỗi cạnh là cạnh chung của đúng hai mặt, nên C = $\large \frac{3M}{2}$ hay 2C = 3M
Hệ thức trên chứng tỏ M là một số chẵn.
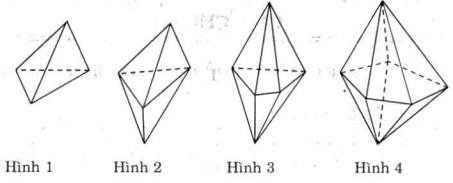
Hình trên là các khối đa diện có các mặt là tam giác:
- Hình 1 là một khối tứ diện có các mặt là tam giác.
- Hình 2 là khối đa diện có 6 mặt, gồm hai khối tứ diện có chung một mặt.
- Hình 3 là khối đa diện có 8 mặt, gồm hai khối chóp tứ giác có chung mặt đáy.
- Hình 4 là khối đa diện có 10 mặt, gồm hai khối chóp ngũ giác có chung mặt đáy.
Bài 2. Chứng minh rằng nếu khối đa diện có mỗi đỉnh là đỉnh chung của ba cạnh thì số đỉnh phải là số chẵn.
Giải
Gọi C là số cạnh và Đ là số đỉnh. Vì có Đ đỉnh, mà mỗi đỉnh là đỉnh chung của 3 cạnh nên số cạnh là 3Đ. Mà cứ mỗi cạnh thì có hai đỉnh, nên ta có .png) . Vậy 2C = 3Đ.
. Vậy 2C = 3Đ.
Hệ thức trên chứng tỏ Đ là một số chẵn.
Bài 3. Chứng minh rằng nếu khối đa diện có các mặt là tam giác và mỗi đỉnh là đỉnh chung của ba cạnh thì đó là khối tứ diện.
Giải
Gọi A là một đỉnh của khối đa diện. Vì A là đỉnh chung của 3 cạnh, ta gọi 3 cạnh đó là AB, AC, AD. Nhưng các mặt của khối đa diện là các tam giác nên các tam giác ABC, ACD, ABD là 3 mặt của khối đa diện. Như thế buộc tam giác BCD là mặt thứ tư của khối đa diện.
Vậy khối đa diện thỏa mãn đề bài là một khối tứ diện.
.png)
Bài 4. Hãy phân chia một khối hộp thành năm khối tứ diện.
Giải
Trong hình dưới, khối hộp ABCD.A'B'C'D' được chia thành 5 khối tứ diện là:
ABDA', BCDC', BA'B'C', DA'C'D', BDA'C'.
.png)
Bài 5. Hãy phân chia một khối tứ diện thành bốn khối tứ diện bởi hai mặt phẳng.
Giải
Xét khối tứ diện ABCD. Trên cạnh AB lấy điểm M (khác với A và B), trên cạnh CD lấy điểm N (khác với C và D). Hai mặt phẳng (ANB) và (CDM) cắt nhau theo giao tuyến MN và hai mặt phẳng này chia khối tứ diện ABCD thành bốn khối tứ diện là: MBCN, MBDN, MACN, MADN.
.png)
