ÔN TẬP CHƯƠNG III
II. BÀI TẬP
Bài 1. Cho bốn điểm A(1; 6; 2), B(4; 0; 6), C(5; 0; 4), D(5; 1; 3).
a) Chứng minh rằng bốn điểm đó không đồng phẳng.
b) Tính thể tích tứ diện ABCD.
c) Viết phương trình mp(BCD).
d) Viết phương trình mặt cầu tâm A tiếp xúc với mp(BCD). Tìm tọa độ tiếp điểm.
Giải
a) Ta có: $\vec{AB}$ = (3; -6; -4), $\vec{AC}$ = (4; -6; 2), $\vec{AD}$ = (4; -5; 1)
[$\vec{AB}$, $\vec{AC}$] = (12; 10; 6) ⇒ [$\vec{AB}$, $\vec{AC}$]. $\vec{AD}$ = 4 $\neq$ 0
Suy ra bốn điểm A, B, C, D không đồng phẳng.
b) $V_{ABCD}$ = $\large \frac{1}{6}$ $\mid$ [$\vec{AB}$, $\vec{AC}$]. $\vec{AD}$$\mid$ = $\large \frac{2}{3}$
c) Ta có: $\vec{BC}$ = (1; 0; -2), $\vec{BD}$ = (1; 1; -3)
Vectơ pháp tuyến của mp(BCD): $\vec{n}$ = [$\vec{BC}$, $\vec{BD}$] = (2; 1; 1)
Phương trình của mặt phẳng (BCD):
2.(x - 4) + 1.(y - 0) + 1.(z - 6) ⇔ 2x + y + z - 14 = 0
d) Gọi (S) là mặt cầu tâm A tiếp xúc với mp(BCD)
Bán kính của (S): R = d(A, (BCD)) = $\large \frac{\mid 2.1+6+2-14\mid }{\sqrt{6}}$ = $\large \frac{4}{\sqrt{6}}$ = $\large \frac{2\sqrt{6}}{3}$
Phương trình của mặt cầu (S): $(x-1)^{2}$ + $(y-6)^{2}$ + $(z-1)^{2}$ = $\large \frac{8}{3}$
Gọi $\Delta$ là đường thẳng qua A và vuông góc với mp(BCD), $\Delta$ có vectơ chỉ phương $\vec{a}$ = $\vec{n}$
Phương trình tham số của đường thẳng $\Delta$: $\left\{\begin{matrix} x=1+2t & & \\ y=6+t & & \\ z=2+t & & \end{matrix}\right.$
Gọi H là tiếp điểm của mp(BCD) và (S) thì H là giao điểm của $\Delta$ và mp(BCD).
Tọa độ của H ứng với t nghiệm đúng phương trình:
2(1 + 2t) + (6 + t) + (2 + t) - 14 = 0 ⇔ t = $\large \frac{2}{3}$
Suy ra tiếp điểm của mp(BCD) và (S) là điểm H($\large \frac{7}{3}$; $\large \frac{20}{3}$; $\large \frac{8}{3}$)
Bài 2. Cho hai điểm A(1; -1; -2), B(3; 1; 1) và mặt phẳng (P): x - 2y + 3z - 5 = 0
a) Tìm tọa độ điểm A' đối xứng với điểm A qua mp(P).
b) Tìm góc giữa đường thẳng AB và mp(P).
c) Viết phương trình mặt phẳng (Q) đi qua A, B và vuông góc với mp(P).
d) Tìm tọa độ giao điểm I của đường thẳng AB và mp(P). Viết phương trình đường thẳng $\Delta$ nằm trong (P), đi qua I và vuông góc với AB.
Giải
a) Gọi d là đường thẳng qua A và vuông góc với mp(P) và H là hình chiếu vuông góc của A trên mp(P) thì H là giao điểm của d và (P). Mặt phẳng (P) có vectơ pháp tuyến $\vec{n_{P}}$ = (1; -2; 3), $\vec{n_{P}}$ chính là vectơ chỉ phương của d.
Phương trình tham số của d: $\left\{\begin{matrix} x=1+t & & \\ y=-1-2t & & \\ z=-2+3t & & \end{matrix}\right.$
Tọa độ của H ứng với t nghiệm đúng phương trình:
(1 + t) - 2(-1 - 2t) + 3(-2 + 3t) – 5 = 0 ⇔ t = $\large \frac{4}{7}$
Suy ra H($\large \frac{11}{7}$; -$\large \frac{15}{7}$; -$\large \frac{2}{7}$)
Vì A' là điểm đối xứng của A qua mp(P) nên H là trung điểm của AA'. Suy ra: tọa độ của A' là:
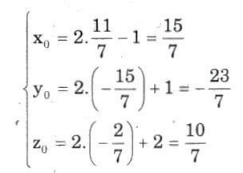
Vậy A'($\large \frac{15}{7}$; -$\large \frac{23}{7}$; -$\large \frac{10}{7}$)
b) Gọi $\varphi$ là góc giữa đường thẳng AB và mp(P)
Đường thẳng AB có vectơ chỉ phương $\vec{a}$ = $\vec{AB}$ = (2; 2; 3)
Ta có: sin$\varphi$ = $\mid$cos($\vec{a}$, $\vec{n}$)$\mid$ = $\large \frac{\mid 7\mid }{\sqrt{14}.\sqrt{17}}$ = $\large \frac{7}{\sqrt{238}}$
c) Mặt phẳng (Q) qua AB và vuông góc với mp(P) nên có vectơ pháp tuyến $\vec{n_{Q}}$ định bởi:
$\vec{n_{Q}}$ = [$\vec{a}$, $\vec{n_{P}}$] = (12; -3; -6), cùng phương với vectơ $\vec{u}$ = (4; -1; -2)
Phương trình mặt phẳng (Q):
4.(x - 1) - 1.(y + 1) - 2.(z + 2) = 0 ⇔ 4x - y - 2z - 9 = 0
d) * Phương trình tham số của đường thẳng AB: $\left\{\begin{matrix} x=1+2t & & \\ y=-1+2t & & \\ z=-2+3t & & \end{matrix}\right.$
Tọa độ của điểm I là giao điểm của đường thẳng AB và mp(P) ứng với t nghiệm đúng phương trình:
(1 + 2t) - 2(-1 + 2t) + 3(-2 + 3t) - 5 = 0 ⇔ t = $\large \frac{8}{7}$
Suy ra: I($\large \frac{23}{7}$; $\large \frac{9}{7}$; $\large \frac{10}{7}$)
* Dễ thấy đường thẳng $\Delta$ đi qua điểm I và có vectơ chỉ phương $\vec{u}$ = (4; -1; -2) nên có phương trình là:
$\large \left\{\begin{matrix} x=\frac{23}{7}+4t & & \\ y=\frac{9}{7}-t & & \\ z=\frac{10}{7}-2t & & \end{matrix}\right.$
Bài 3. Cho đường thẳng d và mặt phẳng (P) có phương trình:
d: $\large \left\{\begin{matrix} x=\frac{2}{3}+t & & \\ y=-\frac{11}{3}+t & & \\ z=t & & \end{matrix}\right.$
(P): x - 3y + z - 1 = 0
a) Viết phương trình đường thẳng d' là hình chiếu vuông góc của d trên mặt phẳng (P).
b) Viết phương trình đường thẳng $d_{1}$ là hình chiếu song song của d trên mặt phẳng (P) theo phương Oz.
c) Viết phương trình đường thẳng đi qua gốc tọa độ O, cắt d và song song với mặt phẳng (P).
Giải
a) Đường thẳng d đi qua điểm M($\large \frac{2}{3}$; -$\large \frac{11}{3}$; 0) và có véctơ chỉ phương $\vec{u}$ = (1; 1; 1)
Mặt phẳng (P) có vectơ pháp tuyến $\vec{n_{P}}$ = (1; -3; 1)
Gọi (Q) là mặt phẳng qua d và vuông góc mặt phẳng (P) thì d' là giao tuyến của (P) và (Q).
Mặt phẳng (Q) có vectơ pháp tuyến là: $\vec{n_{Q}}$ = [$\vec{u}$, $\vec{n_{P}}$] = (4; 0; -4), cùng phương với $\vec{a}$ = (1; 0; -1)
Phương trình (Q):
1.(x - $\large \frac{2}{3}$) - 1.(z – 0) = 0 ⇔ x - z - $\large \frac{2}{3}$ = 0 ⇔ 3x – 3z – 2 = 0
Các điểm nằm trên d' có tọa độ nghiệm đúng hệ phương trình:
$\left\{\begin{matrix} x-3y+z-1=0 & \\ 3x-3z-2=0 & \end{matrix}\right.$ ⇒ J($\large \frac{2}{3}$; -$\large \frac{1}{9}$; 0) $\in$ d'
Đường thẳng d' có vectơ chỉ phương $\vec{v}$ là:
$\vec{v}$ = [$\vec{n_{P}}$, $\vec{a}$] = (3; 2; 3)
Phương trình của đường thẳng d' là: $\large \left\{\begin{matrix} x=\frac{2}{3}+3t & & \\ y=-\frac{1}{9}+2t & & \\ z=3t & & \end{matrix}\right.$
b) Gọi ($\alpha$) là mặt phẳng qua d và song song với trục Oz thì $d_{1}$ là giao tuyến của ($\alpha$) và (P). Mặt phẳng ($\alpha$) qua điểm M($\large \frac{2}{3}$; -$\large \frac{11}{3}$; 0) và có véctơ pháp tuyến là: $\vec{n_{\alpha }}$ = [$\vec{u}$, $\vec{k}$] = (1; -1; 0)
Phương trình của mặt phẳng ($\alpha$):
1.(x - $\large \frac{2}3{}$) - 1.(y + $\large \frac{11}3{}$) =0 ⇔ x - y - $\large \frac{13}{3}$ = 0
Các điểm nằm trên $d_{1}$ có tọa độ nghiệm đúng hệ phương trình:
$\large \left\{\begin{matrix} x-3y+z-1=0 & \\ x-y-\frac{13}{3}=0 & \end{matrix}\right.$ ⇒ K($\large \frac{13}{3}$; 0; -$\large \frac{10}{3}$) $\in$ $d_{1}$
Đường thẳng $d_{1}$ có vectơ chỉ phương là $\vec{w}$ = [$\vec{n_{P}}$, $\vec{n_{\alpha }}$] = (1; 1; 2)
Phương trình của đường thẳng $d_{1}$: $\large \left\{\begin{matrix} x=\frac{13}{3}+t & & \\ y=t & & \\ z=-\frac{10}{3}+2t & & \end{matrix}\right.$
c) Gọi $d_{2}$ là đường thẳng cần tìm
Giả sử $d_{2}$ cắt d tại điểm N, suy ra N($\large \frac{2}{3}$ + t; -$\large \frac{11}{3}$ + t; t)
Do $d_{2}$ đi qua gốc tọa độ O và điểm N nên $d_{2}$ có vectơ chỉ phương là
$\vec{ON}$ = ($\large \frac{2}{3}$ + t; - $\large \frac{11}{3}$ + t; t)
Để đường thẳng $d_{2}$ song song với mặt phẳng (P) thì trước hết ta phải có điều kiện $\vec{ON}$ $\perp$ $\vec{n_{P}}$
Ta có $\vec{ON}$ $\perp$ $\vec{n_{P}}$ ⇔ 1.($\large \frac{2}{3}$ + t) - 3.(-$\large \frac{11}{3}$ + t) + 1.t = 0 ⇔ t = $\large \frac{35}{3}$
Suy ra $\vec{ON}$ = ($\large \frac{37}{3}$; 8; $\large \frac{35}{3}$)
$\vec{ON}$ cùng phương với vectơ $\vec{p}$ = (37; 24; 35)
Vậy phương trình của đường thẳng $d_{2}$ là: $\large \frac{x}{37}$ = $\large \frac{y}{24}$ = $\large \frac{z}{35}$
Bài 4. Cho điểm A(2; 3; 1) và hai đường thẳng:
$d_{1}$: $\left\{\begin{matrix} x=-2-t & & \\ y=2+t& & \\ z=2t & & \end{matrix}\right.$
và $d_{2}$: $\large \frac{x+5}{3}$ = $\large \frac{y-2}{-1}$ = $\large \frac{z}{1}$
a) Viết phương trình mặt phẳng (P) đi qua A và $d_{1}$.
b) Viết phương trình mặt phẳng (Q) đi qua A và $d_{2}$
c) Viết phương trình đường thẳng d đi qua A, cắt cả $d_{1}$ và $d_{2}$.
d) Tính khoảng cách từ A đến $d_{2}$.
Giải
a) Đường thẳng $d_{1}$ qua điểm M(-2; 2; 0), có vectơ chỉ phương $\vec{u}$ = (-1; 1; 2)
Ta có $\vec{MA}$ = (4; 1; 1). Suy ra vectơ pháp tuyến của mp (P) là:
$\vec{n_{P}}$ = [$\vec{MA}$, $\vec{u}$] = (1; -9; 5)
Phương trình của mặt phẳng (P)
1.(x - 2) – 9(y - 3) + 5(z - 1) = 0 ⇔ x - 9y + 5z + 20 = 0
b) Đường thẳng $d_{2}$ đi qua điểm N(-5; 2; 0), có vectơ chỉ phương $\vec{v}$ = (3; -1; 1)
Ta có $\vec{NA}$ = (7; 1; 1). Suy ra vectơ pháp tuyến của mặt phẳng (Q) là:
$\vec{n_{Q}}$ = [$\vec{NA}$, $\vec{v}$] = (2; -4; -10), cùng phương với $\vec{a}$ = (1; -2; -5)
Phương trình của mặt phẳng (Q).
1.(x + 5) - 2(y - 2) - 5(z - 0) = 0 ⇔ x - 2y - 5z + 9 = 0
c) Đường thẳng d chính là giao tuyến của (P) và (Q)
Các điểm nằm trên d nghiệm đúng hệ phương trình:
$\left\{\begin{matrix} x-9x+5x+20=0 & \\ x-2y-5x+9=0 & \end{matrix}\right.$ ⇒ I(-$\large \frac{29}{2}$; 0; -$\large \frac{11}{10}$) $\in$ d
Đường thẳng d có vectơ chỉ phương:
$\vec{w}$ = [$\vec{n_{P}}$, $\vec{a}$] = (55; 10; 7)
Phương trình của đường thẳng d là: $\large \left\{\begin{matrix} x=-\frac{29}{2}+55t & & \\ y=10t & & \\ z=-\frac{11}{10}+7t & & \end{matrix}\right.$
d) Từ kết quả trên ta có $\mid$[$\vec{NA}$, $\vec{v}$]$\mid$ = 2$\sqrt{30}$ và $\mid$$\vec{v}$$\mid$ = $\sqrt{11}$
Suy ra khoảng cách từ A đến $d_{2}$ là: d(A, $d_{2}$) = $\large \frac{2\sqrt{30}}{\sqrt{11}}$
Bài 5. Cho hai đường thẳng:
d: $\large \frac{x}{1}$ = $\large \frac{y-1}{2}$ = $\large \frac{z-6}{3}$
và d': $\left\{\begin{matrix} x=1+t & & \\ y=-2+t & & \\ z=3-t & & \end{matrix}\right.$
a) Chứng minh hai đường thẳng đó chéo nhau. Tìm góc giữa chúng.
b) Tìm khoảng cách giữa d và d'.
c) Viết phương trình đường vuông góc chung của d và d'.
d) Viết phương trình đường thẳng song song với Oz, cắt cả d và d'.
Giải
a) Đường thẳng d đi qua điểm M(0; 1; 6), có vectơ chỉ phương $\vec{u}$ = (1; 2; 3)
Đường thẳng d' qua điểm N(1; -2; 3), có vectơ chỉ phương $\vec{v}$ = (1; 1; -1)
Ta có: [$\vec{u}$, $\vec{v}$] = (-5; 4; -1), $\vec{MN}$ = (1; -3; -3)
Suy ra [$\vec{u}$, $\vec{v}$]. $\vec{MN}$ = -14 $\neq$ 0.
Vậy d và d' chéo nhau.
Do $\vec{u}$, $\vec{v}$ = 0 nên $\vec{u}$ $\perp$ $\vec{v}$ hay góc giữa d và d' là 90°.
b) Từ kết quả trên ta có $\mid$[$\vec{u}$, $\vec{v}$]. $\vec{MN}$$\mid$ = 14 và $\mid$[$\vec{u}$, $\vec{v}$]$\mid$ = $\sqrt{42}$
Vậy khoảng cách giữa d và d' là: H = $\large \frac{14}{\sqrt{42}}$
c) Gọi $\Delta$ là đường vuông góc chung của d và d' thì $\Delta$ có vectơ chỉ phương là $\vec{a}$ = [$\vec{u}$, $\vec{v}$] = (-5; 4; -1)
Gọi (P) là mặt phẳng qua d và $\Delta$, (Q) là mặt phẳng qua d' và $\Delta$, thì $\Delta$ là giao tuyến của (P) và (Q).
+ Mặt phẳng (P) đi qua điểm M và có vectơ pháp tuyến:
$\vec{n_{P}}$ = [$\vec{u}$, $\vec{a}$] = (-14; -14; 14), cùng phương với $\vec{p}$ = (1; 1; -1)
Phương trình của (P)
1.(x - 0) + 1.(y - 1) - 1.(z - 6) = 0 ⇔ x + y - z + 5 = 0
+ Mặt phẳng (Q) đi qua điểm N và có vectơ pháp tuyến:
$\vec{n_{Q}}$ = [$\vec{v}$, $\vec{a}$] = (3; 6; 9), cùng phương với $\vec{q}$ = (1; 2; 3)
Phương trình của (Q)
1.(x - 1) + 2.(y + 2) + 3.(z – 3) = 0 ⇔ x + 2y + 3z - 6 = 0
Các điểm thuộc $\Delta$ có tọa độ nghiệm đúng hệ phương trình:
$\left\{\begin{matrix} x+y-z+5=0 & \\ x+2y+3z-6=0 & \end{matrix}\right.$ ⇒ I(-1; -1; 3)$\in$ $\Delta$
Phương trình của đường vuông góc chung $\Delta$ là: $\left\{\begin{matrix} x=-1-5t & & \\ y=-1+4t & & \\ z=3-t & & \end{matrix}\right.$
d) Gọi T là đường thẳng song song Oz và cắt cả d và d' thì T có vectơ chỉ phương $\vec{k}$ = (0; 0; 1). Gọi ($\alpha$) là mặt phẳng qua T và d, ($\beta$) là mặt phẳng qua T và d' thì T là giao tuyến của ($\alpha$) và ($\beta$).
Mặt phẳng ($\alpha$) đi qua điểm M(0; 1; 6) và có vectơ pháp tuyến
$\vec{n_{\alpha }}$ = [$\vec{k}$, $\vec{u}$] = (-2; 1; 0)
Phương trình của mặt phẳng ($\alpha$):
-2.(x - 0) + 1.(y - 1) = 0 ⇔ 2x – y + 1 = 0
Mặt phẳng ($\beta$) đi qua điểm N(1; -2; 3) và có vectơ pháp tuyến
$\vec{n_{\beta }}$ = [$\vec{k}$, $\vec{v}$] = (-1; 1; 0)
Phương trình của mặt phẳng ($\beta$):
-1.(x - 1) + 1.(y + 2) = 0 ⇔ x - y - 3 = 0
Các điểm thuộc T có tọa độ nghiệm đúng hệ phương trình:
$\left\{\begin{matrix} 2x-y+1=0 & \\ x-y-3=0 & \end{matrix}\right.$ ⇒ J(-4; -7; 0) $\in$ T
Vậy phương trình của đường thẳng T cần tìm là: $\left\{\begin{matrix} x=-4 & & \\ y=-7 & & \\ z=t & & \end{matrix}\right.$
Bài 6. Cho hai đường thẳng
d: $\left\{\begin{matrix} x=7+3t & & \\ y=2+2t & & \\ z=1-2t & & \end{matrix}\right.$
và d': $\large \frac{x-1}{2}$ = $\large \frac{y+2}{-3}$ = $\large \frac{z-5}{4}$
a) Chứng minh rằng d và d' đồng phẳng. Viết phương trình mặt phẳng (P) chứa chúng.
b) Tính thể tích hình tứ diện giới hạn bởi mặt phẳng (P) và ba mặt phẳng tọa độ.
c) Viết phương trình mặt cầu ngoại tiếp tứ diện nói trên.
Giải
a) Đường thẳng d đi qua điểm M(7; 2; 1), có vectơ chỉ phương $\vec{u}$ = (3; 2; -2)
Đường thẳng d' đi qua điểm N(1; -2; 5), có vectơ chỉ phương $\vec{v}$ = (2; -3; 4)
Ta có [$\vec{u}$, $\vec{v}$] = (2; -16; -13), $\vec{MN}$ = (-6; -4; 4)
Suy ra [$\vec{u}$, $\vec{v}$].$\vec{MN}$ = 0.
Vậy hai đường thẳng d và d' là đồng phẳng.
Mặt phẳng (P) chứa d và d' có vectơ pháp tuyến $\vec{n}$ = [$\vec{u}$, $\vec{v}$] = (2; -16; -13)
Phương trình của (P)
2(x - 7) - 16(y - 2) - 13(z - 1) = 0 ⇔ 2x - 16y - 13z + 31 = 0 (*)
b) Gọi A, B, C là giao điểm của (P) với các trục Ox, Oy, Oz. Tứ diện OABC là tứ diện giới hạn bởi (P) và ba mặt phẳng tọa độ.
Trong (*) cho y = 0, z = 0 ta được x = -$\large \frac{31}{2}$
Suy ra (P) cắt trục Ox tại điểm A(-$\large \frac{31}{2}$; 0; 0)
Tương tự (P) cắt trục Oy, Oz tại các điểm B(0; $\large \frac{31}{16}$; 0), C(0; 0; $\large \frac{31}{13}$)
Thể tích V của khối tứ diện là:
V = $\large \frac{1}{6}$.OA.OB.OC = $\large \frac{1}{6}$.$\large \frac{31}{2}$.$\large \frac{31}{16}$.$\large \frac{31}{13}$ = $\large \frac{29791}{2496}$
c) Phương trình của mặt cầu (S) ngoại tiếp tứ diện OABC có dạng:
$x^{2}$ + $y^{2}$ + $z^{2}$ + 2ax + 2by + 2cz + d = 0
Do (S) qua các điểm O, A, B, C ta suy ra được:
d = 0, a = $\large \frac{31}{4}$, b = -$\large \frac{31}{32}$x, c = $\large \frac{31}{26}$
Vậy phương trình của mặt cầu (S) là:
$x^{2}$ + $y^{2}$ + $z^{2}$ + $\large \frac{31}{2}$x - $\large \frac{31}{6}$y - $\large \frac{31}{13}$z = 0
Bài 7. Cho hai đường thẳng:
d: $\left\{\begin{matrix} x=t & & \\ y=3 & & \\ z=6+t & & \end{matrix}\right.$
và d': $\left\{\begin{matrix} x=2+t & & \\ y=1-t & & \\ z=2-t & & \end{matrix}\right.$
a) Chứng minh rằng d và d' chéo nhau và vuông góc với nhau.
b) Viết phương trình mặt phẳng (P) đi qua d và vuông góc với d', phương trình của mặt phẳng (Q) đi qua d' và vuông góc với d.
c) Viết phương trình chính tắc của đường vuông góc chung của d và d'.
Giải
a) Đường thẳng d đi qua điểm M(0; 3; 6), có vectơ chỉ phương $\vec{u}$ = (1; 0; 1)
Đường thẳng d' đi qua điểm N(2; 1; 2), có vectơ chỉ phương $\vec{v}$ = (1; -1; -1)
Ta có [$\vec{u}$, $\vec{v}$] = (1; 2; -1), $\vec{MN}$ = (2; -1; -4)
Suy ra [$\vec{u}$, $\vec{v}$].$\vec{MN}$ = 2 $\neq$ 0
Do đó hai đường thẳng d và d' chéo nhau.
Mặt khác $\vec{u}$.$\vec{v}$ = 0 nên $\vec{u}$ $\perp$ $\vec{v}$
Vậy: hai đường thẳng d và d' chéo nhau và vuông góc nhau.
b) Mặt phẳng (P) qua d và vuông góc với d' nên M(0; 3; 6) $\in$ (P) và (P) có vectơ pháp tuyến là $\vec{v}$ = (1; -1; -1).
Phương trình của mặt phẳng (P) là:
1.(x - 0) – 1.(y - 3) - 1.(z - 6) = 0 ⇔ x - y - z + 9 = 0
Tương tự phương trình của mặt phẳng (Q) là:
1.(x - 2) + 1(z - 2) = 0 ⇔ x + z - 4 = 0
c) Gọi $\Delta$ là đường vuông góc chung của d và d' thì $\Delta$ là giao tuyến của (P) và (Q).
- $\Delta$ có vectơ chỉ phương là $\vec{a}$ = [$\vec{u}$, $\vec{v}$] = (1; 2; -1)
- Tọa độ các điểm thuộc $\Delta$ nghiệm đúng hệ phương trình:
$\left\{\begin{matrix} x-y-z+9=0 & \\ x+z-4=0 & \end{matrix}\right.$ ⇒ I(0; 5; 4) $\in$ $\Delta$
Phương trình chính tắc của đường vuông góc chung $\Delta$ là:
$\large \frac{x}{1}$ = $\large \frac{y-5}{2}$ = $\large \frac{z-4}{-1}$
Bài 8. Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình:
(P): 2x – y + z + 2 = 0 và (Q): x + y + 2z - 1 = 0
a) Chứng minh rằng (P) và (Q) cắt nhau. Tìm góc giữa hai mặt phẳng đó.
b) Viết phương trình đường thẳng d đi qua A(1; 2; -3), song song với cả (P) và (Q).
c) Viết phương trình mặt phẳng (R) đi qua B(-1; 3; 4) vuông góc với cả (P) và (Q).
Giải
a) Mặt phẳng (P) đi qua điểm M(0; 0; -2) và có vectơ pháp tuyến $\vec{n_{P}}$ = (2; -1; 1)
Mặt phẳng (Q) đi qua điểm N(0; 1; 0) và có vectơ pháp tuyến $\vec{n_{Q}}$ = (1; 1; 2)
Do $\vec{n_{P}}$. $\vec{n_{Q}}$ = 3 $\neq$ 0 nên hai mặt phẳng (P) và (Q) cắt nhau.
b) Đường thẳng d đi qua A(1; 2; -3) song song với cả (P) và (Q) có vectơ chỉ phương là:
$\vec{u}$ = [$\vec{n_{P}}$, $\vec{n_{Q}}$] = (-3; -3; 3), cùng phương với $\vec{v}$ = (1; 1; -1)
Phương trình của đường thẳng d là:
$\large \frac{x-1}{1}$ = $\large \frac{y-2}{1}$ = $\large \frac{z+3}{-1}$
c) Mặt phẳng (R) qua B(-1; 3; 4) vuông góc với cả (P) và (Q) có vectơ pháp tuyến là
$\vec{v}$ = (1; 1; -1). Vậy phương trình của mặt phẳng (R) là:
1.(x + 1) + 1.(y - 3) - 1.(z - 4) = 0 ⇔ x + y - z + 2 = 0
Bài 9. Cho mặt cầu (S) có phương trình: $x^{2}$ + $y^{2}$ + $z^{2}$ - 2x - 4y - 6z = 0.
a) Tìm tọa độ tâm mặt cầu và tính bán kính mặt cầu
b) Tùy theo giá trị của k, hãy xét vị trí tương đối của mặt cầu (S) và mặt phẳng (P) với (P): x + y − z + k = 0
c) Mặt cầu cắt ba trục Ox, Oy, Oz lần lượt tại ba điểm A, B, C khác với gốc tọa độ O. Viết phương trình mặt phẳng (ABC).
d) Viết phương trình mặt phẳng tiếp xúc với mặt cầu (S) tại điểm B.
e) Viết phương trình mặt phẳng tiếp xúc với mặt cầu (S) và song song với mặt phẳng (Q) có phương trình 4x + 3y - 12z - 1 = 0.
Giải
a) Phương trình của mặt cầu (S) viết lại:
$(x-1)^{2}$ + $(y-2)^{2}$ + $(z-3)^{2}$ = 14
Vậy (S) có tâm I(1; 2; 3) và bán kính R = $\sqrt{14}$
b) Khoảng cách từ I đến mặt phẳng (P): d = $\large \frac{\mid 1+2-3+k\mid }{\sqrt{3}}$ = $\large \frac{\mid k\mid }{\sqrt{3}}$
Do đó ta có kết luận sau:
• (P) và (S) không có điểm chung khi và chỉ khi:
d > R ⇔ $\large \frac{\mid k\mid }{\sqrt{3}}$ > $\sqrt{14}$ ⇔ k < -$\sqrt{42}$ hoặc k > $\sqrt{42}$
• (P) và (S) tiếp xúc với nhau khi và chỉ khi:
d = R ⇔ $\large \frac{\mid k\mid }{\sqrt{3}}$ = $\sqrt{14}$ ⇔ k = -$\sqrt{42}$ hoặc k = $\sqrt{42}$
• (P) và (S) cắt nhau khi và chỉ khi:
d < R ⇔ $\large \frac{\mid k\mid }{\sqrt{3}}$ < $\sqrt{14}$ ⇔ -$\sqrt{42}$ < k < $\sqrt{42}$
c) Phương trình định hoành độ điểm chung của (S) với trục hoành:
$x^{2}$ - 2x = 0 ⇔ x = 0 hoặc x = 2
Suy ra (S) cắt trục Ox tại điểm A(2; 0; 0) (khác gốc tọa độ O)
Tương tự ta được B(0; 4; 0), C(0; 0; 6)
Áp dụng phương trình theo đoạn chắn, phương trình của mặt phẳng (ABC) là:
$\large \frac{x}{2}$ + $\large \frac{y}{4}$ + $\large \frac{z}{6}$ = 1 ⇔ 6x + 3y + 2z - 12 = 0
d) Gọi ($\alpha$) là mặt phẳng tiếp xúc với (S) tại điểm B(0; 4; 0) thì ($\alpha$) có vectơ pháp tuyến là $\vec{n_{\alpha }}$ = $\vec{IB}$ = (-1; 2; -3).
Phương trình của tiếp diện ($\alpha$) là:
-1.(x - 0) + 2.(y - 4) - 3.(z - 0) = 0 ⇔ x - 2y + 3z + 8 = 0
e) Phương trình mặt phẳng ($\beta$) song song với mặt phẳng (Q) có dạng:
4x + 3y - 12z + m = 0
Mặt phẳng ($\beta$) tiếp xúc với (S) khi và chỉ khi:
d(I, ($\beta$)) = R ⇔ $\large \frac{\mid 4.1+3.2-12.3+m\mid }{13}$ = $\sqrt{14}$
⇔ $\mid$m-26$\mid$ = 13$\sqrt{14}$ ⇔ m = .png)
Vậy có hai tiếp diện của (S) phương trình là:
4x + 3y - 12z + 26 + 13$\sqrt{14}$ = 0
hoặc 4x + 3y - 12z + 26 - 13$\sqrt{14}$ = 0
Bài 10. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Trên các tia AA', AB, AD (có chung gốc A) lần lượt lấy các điểm M, N, P khác A sao cho AM = m, AN = n và AP = p.
a) Tìm sự liên hệ giữa m, n và p sao cho mặt phẳng (MNP) đi qua đỉnh C' của hình lập phương.
b) Trong trường hợp mặt phẳng (MNP) luôn đi qua C', hãy tìm thể tích bé nhất của tứ diện AMNP. Khi đó tứ diện AMNP có tính chất gì?
Giải
.png)
a) Chọn hệ Oxyz sao cho A trùng với gốc tọa độ O, B(1; 0; 0), D(0; 1; 0) và A'(0; 0; 1).
Suy ra C'(1; 1; 1)
Từ giả thiết ta suy ra M(0; 0; m), N(n; 0; 0), P(0; p; 0).
Phương trình của mặt phẳng (MNP) $\large \frac{x}{n}$ + $\large \frac{y}{p}$ + $\large \frac{z}{m}$ = 1
Mặt phẳng (MNP) đi qua điểm C'(1; 1; 1) khi và chỉ khi:
$\large \frac{1}{m}$ + $\large \frac{1}{n}$ + $\large \frac{1}{p}$ = 1
b) Gọi V là thể tích khối tứ diện AMNP ta có:
V = $\large \frac{1}{6}$AM.AN.AP = $\large \frac{1}{6}$mnp
Áp dụng bất đẳng thức Côsi:
$\large \frac{1}{m}$ + $\large \frac{1}{n}$ + $\large \frac{1}{p}$ $\geq$ 3.$\sqrt[3]{\frac{1}{mnp}}$ ⇔ mnp $\geq$ 27
Do đó V $\geq$ $\large \frac{9}{2}$
Đẳng thức xảy ra khi và chỉ khi m = n = p = 3
Vậy minV = $\large \frac{9}{2}$ khi m = n = p = 3
Khi đó tứ diện AMNP có ba mặt tại A là các tam giác vuông cân bằng nhau với AM = AN = AP = 3
