§4. THỂ TÍCH CỦA KHỐI ĐA DIỆN
B. CÂU HỎI VÀ BÀI TẬP
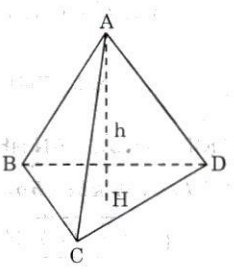
Bài 15. Cho tam giác ABC cố định và một điểm S thay đổi. Thể tích của khối chóp S.ABC có thay đổi hay không nếu:
a) Đỉnh S di chuyển trên một mặt phẳng song song với mặt phẳng (ABC)?
b) Đỉnh S di chuyển trên một mặt phẳng song song với chỉ một cạnh đáy?
c) Đỉnh S di chuyển trên một đường thẳng song song với một cạnh đáy?
Giải
Gọi h là chiều cao và V là thể tích của khối chóp S.ABC
Ta có: V = $\frac{1}{3}$$S_{(ABC)}$.h
a) Nếu S di chuyển trên một mặt phẳng (P) || (ABC) thì h bằng với khoảng cách giữa hai mặt phẳng (ABC) và (P) nên h không đổi, do đó V cũng không đổi.
b) Nếu S di chuyển trên một mặt phẳng (P) song song với chỉ một cạnh của tam giác ABC thì (P) có thể không song song với (ABC), do đó h thay đổi. Vậy thể tích V thay đổi.
c) Nếu S di chuyển trên một đường thẳng $\Delta$ song song với một cạnh đáy, chẳng hạn như cạnh AB ($\Delta$ phải không nằm trên mặt phẳng (ABC)), khi đó đường thẳng $\Delta$ song song với mặt phẳng (ABC), do đó khoảng cách h không đổi, vậy V cũng không đổi.
Bài 16. Hãy chia một khối tứ diện thành hai khối tứ diện sao cho tỉ số thể tích của hai khối tứ diện này bằng một số k > 0 cho trước.
Giải
Ta xét khối tứ diện ABCD. Trên cạnh CD lấy điểm M sao cho $\frac{MC}{MD}$ = k ⇔ MC = kMD.
Gọi h là khoảng cách từ A đến mặt phẳng (BCD), $V_{1}$ và $V_{2}$ lần lượt là thể tích các khối tứ diện ABCM và ABDM
Ta có:
.png)
Suy ra:
.png)
Vậy ta đã chia khối tứ diện ABCD thành hai khối tứ diện ABCM và ABDM với tỉ số thể tích $\frac{V_{1}}{V_{2}}$ = k
.png)
Bài 17. Tính thể tích của khối hộp ABCD.A'B'C'D' biết rằng AA'B'D' là khối tứ diện đều cạnh a.
Giải
* Trước hết ta tính thể tích của một khối tứ diện đều cạnh a.
Ta xét khối tứ diện đều MNPQ.
Vì MNPQ là khối tứ diện đều nên M.NPQ là khối chóp tam giác đều.
Kẻ đường cao MH thì H là tâm của $\Delta$NPQ. Gọi I là trung điểm của PQ thì NI là đường cao của $\Delta$NPQ, suy ra
NH = $\frac{2}{3}$NI = $\frac{a\sqrt{3}}{3}$
MH $\perp$ (NPQ) ⇒ MH $\perp$ NH ⇒ $\Delta$MHN vuông tại H
Do đó
.png)
Suy ra h = MN = $\frac{a\sqrt{6}}{3}$
Gọi $V_{1}$ là thể tích khối tứ diện đều MNPQ ta có:
.png)
.png)
* Kế tiếp ta chứng minh rằng, có thể chia một khối hộp ABCD.A'B'C'D' thành sáu khối tứ diện có thể tích bằng nhau.
.png)
• Trước hết chia khối hộp thành hai khối lăng trụ là ABC.A'B'C' và ACD.A'C'D'
Dễ thấy hai khối lăng trụ này có thể tích bằng nhau, vì có đáy bằng nhau và có cùng chiều cao.
• Tiếp tục ta chia khối lăng trụ ACD.A'C'D' thành ba khối tứ diện là ACDC', AA'C'D', ADC'D'.
Hai khối tứ diện ACDC', AA'C'D' có thể tích bằng nhau vì có hai đáy là $\Delta$ACD và $\Delta$A'C'D' bằng nhau, có cùng chiều cao h là khoảng cách giữa (ABCD) và (AA'C'D').
Hai khối tứ diện ACDC' và ADC'D' có thể tích bằng nhau vì chúng có hai đáy là hai tam giác CDC' và DC'D' bằng nhau và có cùng chiều cao là khoảng cách từ A đến mp(CDD'C').
Như vậy, khối lăng trụ ACD.A'C'D' được chia thành ba khối tứ diện có thể tích bằng nhau.
Suy ra khối hộp ABCD.A'B'C'D' được chia thành sáu khối tứ diện có thể tích bằng nhau. Từ kết quả trên ta suy ra V = 6.$V_{(AA'B'D')}$.
Mà AA'B'D' là khối tứ diện đều cạnh a nên có thể tích bằng .png)
Vậy .png)
Bài 18. Tính thể tích của khối lăng trụ n-giác đều có tất cả các cạnh đều bằng a.
Giải
Ta xét khối lăng trụ (T) n-giác đều có tất cả các cạnh đều bằng a, đáy là đa giác đều (G) có n cạnh. Gọi (V) là thể tích của (T), ta có V=$S_{(G)}$.h
+ h = a.
+ (G) là đa giác đều n cạnh nên có diện tích là .png)
Vậy thể tích V của khối lăng trụ là:
.png)
Bài 19. Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại A, AC = b, $\widehat{ACB}$ = 60°. Đường thẳng BC' tạo với mp(AA'CC') một góc 30°.
a) Tính độ dài đoạn thẳng AC'.
b) Tính thể tích khối lăng trụ đã cho.
Giải
a) Từ giả thiết ta suy ra AB $\perp$ AC và AB $\perp$ AA'
Suy ra AB $\perp$ (ACC'A'), do đó AC' là hình chiếu vuông góc của BC' trên mặt phẳng (AA'CC')
Do vậy $\widehat{AC'B}$ = 30°.
Gọi x là độ dài cạnh bên của khối lăng trụ. Tam giác ABC là nửa tam giác đều nên BC = 2AC = 2b
Từ tam giác BCC' vuông tại C:
.png)
Từ tam giác ABC' vuông tại A:
.png)
Từ tam giác ACC' vuông tại C:
.png)
Do đó
.png)
Từ (1) và (2):
.png)
Suy ra $AC'^{2}$=9$b^{2}$. Vậy AC' = 3b
b) Gọi V là thể tích khối lăng trụ đã cho, ta có:
.png)
Vậy thể tích của khối lăng trụ là V = $\sqrt{6}$$b^{3}$.
.png)
Bài 20. Cho khối lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều cạnh a, điểm A' cách đều ba điểm A, B, C, cạnh bên AA' tạo với mặt phẳng đáy một góc 60°.
a) Tính thể tích của khối lăng trụ đó.
b) Chứng minh rằng mặt bên BCC'B' là một hình chữ nhật.
c) Tính tổng diện tích các mặt bên của hình lăng trụ ABC.A'B'C' (tổng đó gọi là diện tích xung quanh của hình (hoặc khối) lăng trụ đã cho).
Giải
a) Gọi H là hình chiếu vuông góc của A' trên mp(ABC). Do A' cách đều A, B, C nên H là tâm của $\Delta$ABC
Từ giả thiết suy ra $\widehat{A'AH}$ = 60°.
Gọi I là trung điểm của BC thì AI $\perp$ BC.
Ta có: .png)
Từ tam giác AA'H vuông tại H:
A'H = AHtan60° = $\frac{a\sqrt{3}}{3}$.$\sqrt{3}$ = a
Thể tích khối lăng trụ ABC.A'B'C' là:
.png)
.png)
b) Tứ giác BCC'B' là mặt bên của khối lăng trụ nên là hình bình hành. Mặt khác:
BC $\perp$ AI và BC $\perp$ HA' nên BC $\perp$ mp(AA'I).
Suy ra BC $\perp$ AA'.
Mà BB' // AA' nên BC $\perp$ BB'.
Vậy mặt bên BCC'B' là một hình chữ nhật.
c) Tam giác AA'H là nửa tam giác đều nên AA' = 2AH = $\frac{2\sqrt{3}a}{3}$
Goi J là hình chiếu vuông góc của B trên canh AA'.
Ta có: AA' $\perp$ BJ và AA' $\perp$ BC nên AA' $\perp$ (BCJ).
Suy ra AA' $\perp$ CJ và AA' $\perp$ IJ.
Tam giác AIJ là nửa tam giác đều, suy ra .png)
Từ tam giác ABJ vuông tại J:
.png)
Gọi Sxq là diện tích xung quanh của khối lăng trụ, ta có:
.png)
Bài 21. Cho điểm M nằm trong hình tứ diện đều ABCD. Chứng minh rằng tổng các khoảng cách từ M tới bốn mặt của hình tứ diện là một số không phụ thuộc vào vị trí của điểm M. Tổng đó bằng bao nhiêu nếu cạnh của tứ diện đều bằng a?
Giải
Gọi $h_{1}$, $h_{2}$, $h_{3}$, $h_{4}$ là các khoảng cách từ M đến các mặt phẳng (BCD), (ACD), (ABD), (ABC)
Ta chia khối tứ diện ABCD thành bốn khối chóp nhỏ là:
M.BCD, M.ACD, M.ABD, M.ABC và gọi $V_{1}$, $V_{2}$, $V_{3}$, $V_{4}$ lần lượt là thể tích của chúng. Vì ABCD là khối tứ diện đều nên các mặt là các tam giác đều và bằng nhau, gọi S là diện tích của chúng.
Ta có: $V_{(ABCD)}$ = $V_{1}$ + $V_{2}$ + $V_{3}$ + $V_{4}$
hay .png)
⇔ h = $h_{1}$ + $h_{2}$ + $h_{3}$ + $h_{4}$ (h là chiều cao của khối tứ diện ABCD)
Vậy: Tổng khoảng cách từ M đến các mặt của khối tứ diện là
$h_{1}$ + $h_{2}$ + $h_{3}$ + $h_{4}$ = $\frac{a\sqrt{6}}{3}$
(h = $\frac{a\sqrt{6}}{3}$ theo kết quả của bài tập 17).
.png)
Bài 22. Cho khối lăng trụ tam giác đều ABC.A'B'C'. Gọi M là trung điểm của AA'. Mặt phẳng đi qua M, B', C chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó.
Giải
Mặt phẳng (MB'C) chia khối lăng trụ thành hai khối chóp là C.ABB'M và B'.C'A'MC.
Do ABC.A'B'C' là khối lăng trụ tam giác đều nên khoảng cách từ C đến mp(ABB'M) và khoảng cách từ B' đến mp(C'A'MC).
Mặt khác ABB'M và C'A'MC là hai hình thang bằng nhau, nên hai khối chóp trên có thể tích bằng nhau.
Suy ra, tỉ số thể tích của hai phần theo đề bài là 1.
.png)
Bài 23. Cho khối chóp tam giác S.ABC. Trên ba đường thẳng SA, SB, SC lần lượt lấy ba điểm A', B', C' khác với S. Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S.A'B'C'. Chứng minh rằng:
.png)
Giải
Đặt $\widehat{BSC}$ = $\alpha$. Gọi H, H' lần lượt là hình chiếu vuông góc của A, A' trên mặt phẳng (SBC), dễ thấy ba điểm S, H, H' thẳng hàng. Ta có:
.png)
.png)
Mặt khác trong mp(SAH) ta có:
.png)
Suy ra:
.png)
.png)
Bài 24. Khối chóp S.ABCD có đáy là hình bình hành, M là trung điểm của cạnh SC. Mặt phẳng (P) đi qua AM, song song với BD, chia khối chóp thành hai phần. Tính tỉ số thể tích của hai phần đó.
Giải
Mặt phẳng (P) song song với BD nên cắt mặt phẳng (SBD) $\supset$ BD theo giao tuyến NQ // BD (N $\in$ SB, Q $\in$ SD).
Như thế (P) cắt khối chóp S.ABCD theo thiết diện là tứ giác ANMQ.
Gọi O = AC $\cap$ BD và I = AM $\cap$ NQ, dễ thấy ba điểm S, I, O thẳng hàng.
Nhận thấy I là trọng tâm của $\Delta$SAC nên $\frac{SI}{SO}$=$\frac{2}{3}$
Trong $\Delta$SBD, NQ // BD ⇒ .png)
Gọi V, $V_{1}$ lần lượt là thể tích các khối chóp S.ABCD và S.ANMQ
Vì ABCD là hình bình hành nên $\Delta$ACB = $\Delta$CAD. Do đó:
.png)
Suy ra thể tích phần còn lại của khối chóp S.ABCD là .png)
Vậy tỉ số thể tích của hai phần theo đề bài là .png)
.png)
Bài 25. Chứng minh rằng nếu có phép vị tự tỉ số k biển tứ diện ABCD thành tứ diện A'B'C'D' thì .png)
Giải
.png)
Giả sử ta có phép vị tự V tỉ số k biến tứ diện ABCD thành tứ diện A'B'C'D'
Suy ra V biến AB thành A'B'. Do đó AB và A'B' nằm trên hai đường thẳng song song hoặc trùng nhau và .png) .
.
Như thế trên đường thẳng chứa AB ta có thể lấy điểm $B_{1}$ sao cho $\vec{AB_{1}}$ = $\vec{A'B'}$. Suy ra .png) .
.
Tương tự ta có thể lấy điểm $C_{1}$ trên đường thẳng chứa AC và điểm $D_{1}$ trên đường thẳng chứa AD sao cho $\vec{AC_{1}}$ = $\vec{A'C'}$, $\vec{AD_{1}}$ = $\vec{A'D'}$ và ta cũng có .png)
Dễ dàng chứng minh được hai tứ diện A$B_{1}$$C_{1}$$D_{1}$ và A'B'C'D' có các cạnh tương ứng bằng nhau nên chúng bằng nhau. Do đó:
.png)
