ÔN TẬP CHƯƠNG II
II. BÀI TẬP
Bài 1. Cho mp(P) và điểm A không thuộc (P). Chứng minh rằng mọi mặt cầu đi qua A và có tâm nằm trên (P) luôn luôn đi qua hai điểm cố định.
Giải
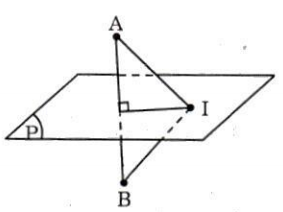
Trên mặt phẳng (P) lấy điểm I bất kì. Gọi B là điểm đối xứng của A qua mặt phẳng (P). Do A cố định nên B cố định và IA = IB. Như vậy mặt cầu (S) có tâm I qua A cũng qua B. Vậy mặt cầu (S) đi qua A và có tâm I $\in$ (P) luôn qua hai điểm cố định A và B.
Bài 2. Xác định tâm và tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC, biết SA = SB = SC = a, $\widehat{ASB}$ = 60°, $\widehat{BSC}$ = 90°, $\widehat{CSA}$ = 120°
Giải
.png)
Áp dụng định lí hàm số côsin trong $\Delta$SAC:
$AC^{2}$ = $SA^{2}$ + $SC^{2}$ - 2SA.SC.cos120°
$AB^{2}$ = $a^{2}$ + $a^{2}$ – 2$a^{2}$($\large \frac{-1}{2}$) = 3$a^{3}$
⇒ AB = a$\sqrt{3}$
Tam giác SAB đều nên AB = a.
Tam giác SBC vuông cân tại S nên BC = a$\sqrt{2}$
Suy ra $AC^{2}$ = $AB^{2}$ + $BC^{2}$. Vậy tam giác ABC vuông tại B, Hạ đường cao SH của hình chóp, do SA = SB = SC = au nên HA = HB = HC, do đó H là trung điểm của AC, suy ra SH là trục của đường tròn ngoại tiếp của tam giác ABC. Gọi K là trung điểm của SA, qua K dựng mặt phẳng (P) là mặt trung trực của SA, gọi O là giao điểm của đường thẳng SH và (P) thì O là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
Hai tam giác vuông SKO và SHA đồng dạng nên ta có:
$\large \frac{SO}{SA}$ = $\large \frac{SK}{SH}$ ⇒ SO = $\large \frac{SK.SA}{SH}$ = $\large \frac{SA^{2}}{2SH}$ = $\large \frac{a^{2}}{2.\frac{a}{2}}$ = a (SH = $\large \frac{a}{2}$)
Vậy bán kính của mặt cầu ngoại tiếp hình chóp S.ABC là R = a
Chú ý rằng O là điểm đối xứng của S qua trung điểm H của AC.
Bài 3. Cho hai đường tròn (O; r) và (O'; r') cắt nhau tại hai điểm A, B và lần lượt nằm trên hai mặt phẳng phân biệt (P) và (P').
a) Chứng minh rằng có mặt cầu (S) đi qua hai đường tròn đó.
b) Tính bán kính R của mặt cầu (S) khi r = 5, r' = $\sqrt{10}$, AB = 6, OO' = $\sqrt{21}$
Giải
.png)
a) Hai đường tròn (O) và (O') cùng đi qua A, B nên tâm O và O' của chúng nằm trên trung trực (P) của đoạn thẳng AB. Dựng trục $\Delta$ và $\Delta$' của hai đường tròn (O) và (O'), dĩ nhiên $\Delta$ và $\Delta$' nằm trên (P). Gọi I là giao điểm của $\Delta$ và $\Delta$' thì I là tâm của mặt cầu (S) đi qua (O) và (O'). Vậy luôn tồn tại mặt cầu (S) đi qua (O) và (O'), bán kính của (S) là R = IA.
b) Gọi K là trung điểm của AB. Ta có:
OK = $\sqrt{OA^{2}-KA^{2}}$ = $\sqrt{25-9}$ = 4
O'K = $\sqrt{O'A^{2}-KA^{2}}$ = $\sqrt{10-9}$ = 1
Vì IO $\perp$ KO và IO' $\perp$ KO' nên tứ giác IOKO' nội tiếp trong đường tròn (T) đường kính IK, (T) cũng là đường tròn ngoại tiếp của $\Delta$OKO'.
Áp dụng định lí hàm số cosin trong $\Delta$OKO':
$OK^{2}$ + $O'K^{2}$ – 2OK.O'K.cos $\widehat{OKO'}$ = $OO'^{2}$
⇔ 16 +1 - 2.4.1.cos$\widehat{OKO'}$ = 21
Suy ra cos$\widehat{OKO'}$ = $\large \frac{-1}{2}$ ⇒ $\widehat{OKO'}$ = 120°
Áp dụng định lí hàm số sin trong $\Delta$OKO':
.png)
Vậy bán kính của mặt cầu (S) là:
R = $\sqrt{IK^{2}+KA^{2}}$ = $\sqrt{28+9}$ = $\sqrt{37}$
Bài 4. Cho một hình nón .png)
sinh bởi một tam giác đều cạnh a khi quay quanh một đường cao của tam giác đó.
a) Một mặt cầu có diện tích bằng diện tích toàn phần của hình nón .png)
thì có bán kính bằng bao nhiêu?
b) Một khối cầu có thể tích bằng thể tích của khối nón .png)
thì có bán kính bằng bao nhiêu?
Giải
a) Khi cho tam giác đều cạnh a quay quanh đường cao của nó, ta được một hình nón .png)
có bán kính r = $\large \frac{a}{2}$, đường sinh l = a, và chiều cao h = $\large \frac{a\sqrt{3}}{2}$
Diện tích toàn phần của hình nón:
Stp = $\pi$r(l + r) = $\pi$$\large \frac{a}{2}$(a + $\large \frac{a}{2}$) = $\large \frac{3}{4}$$\pi$$a^{2}$
Gọi R là bán kính của mặt cầu (S), ta có:
4$\pi$$R^{2}$ = $\large \frac{3}{4}$$\pi$$a^{2}$ ⇔ R = $\large \frac{a\sqrt{3}}{4}$
b) Thể tích khối nón .png)
:
.png)
Gọi R là bán kính của khối cầu (S), ta có:
.png)
Bài 5. Cho tam giác ABC vuông tại A, AB = c, AC = b. Gọi $V_{1}$, $V_{2}$, $V_{3}$ là thể tích các khối tròn xoay sinh bởi tam giác đó (kể cả các điểm trong) khi lần lượt quay quanh AB, AC, BC.
a) Tính $V_{1}$, $V_{2}$, $V_{3}$ theo b, c.
b) Chứng minh rằng .png)
Giải
.png)
a) Kẻ đường cao AH của tam giác ABC. Tam giác ABC vuông tại A nên $a^{2}$ = $b^{2}$ + $c^{2}$. (gọi a = BC)
* Khi cho $\Delta$ABC quay quanh cạnh BC ta được hai khối nón tròn xoay có chung đường tròn đáy, bán kính là AH, chiều cao là BH và CH. Thể tích khối này là:
$V_{3}$ = $\frac{1}{3}\pi AH^{2}.BH$ + $\frac{1}{3}\pi AH^{2}.CH$
= $\frac{1}{3}\pi AH^{2}(BH+CH)$ = $\frac{1}{3}\pi AH^{2}.BC$
Mà AH.BC = AB.AC ⇒ AH = $\large \frac{bc}{a}$ = $\large \frac{bc}{\sqrt{b^{2}+c^{2}}}$
Do đó $V_{3}$ = $\large \frac{\pi b^{2}c^{2}}{3\sqrt{b^{2}+c^{2}}}$
* Khi cho $\Delta$ABC quay xung quanh cạnh AB ta được một khối nón tròn xoay có bán kính đáy AC = b và chiều cao AB = c.
Thể tích khối tròn xoay này là $V_{1}$ = $\large \frac{1}{3}\pi b^{2}c$
* Tương tự $V_{2}$ = $\large \frac{1}{3}\pi c^{2}b$.
b) Ta có:
.png)
So sánh (1) và (2) ta được: .png)
Bài 6. Một hình thang cân ABCD có các cạnh đáy AB = 2a, DC = 4a, cạnh bên AD = BC = 3a. Cho hình thang đó (kể cả các điểm trong) quay quanh trục đối xứng của nó. Hãy tính thể tích và diện tích toàn phần của khối tròn xoay được tạo thành.
Giải
.png)
Gọi K, H lần lượt là trung điểm của AB và CD. Đường thẳng KH là trục của hình thang cân ABCD. Khi cho hình thang này quay xung quanh KH ta được một khối nón cụt có bán kính các đáy là R = 2a, R' = a, chiều cao h = KH.
Ta có KH = $\sqrt{(3a)^{2}-a^{2}}$ = 2$\sqrt{2}$a
Gọi I là giao điểm của hai đường thẳng BC và AD, suy ra IK = KH.
* Thể tích khối nón cụt này là:
V = $\large \frac{1}{3}$$\pi$$DC^{2}$.IH - $\large \frac{1}{3}$$\pi$$KB^{2}$.IK
= $\large \frac{1}{3}$$\pi$.4$a^{2}$.4a$\sqrt{2}$a - $\large \frac{1}{3}$$\pi$.$a^{2}$.2a$\sqrt{2}$a
V = $\large \frac{14\sqrt{2}}{3}$$\pi$$a^{3}$
* Diện tích toàn phần của khối tròn xoay:
Stp = $\pi$HC.IC - $\pi$KB.IB + $\pi$$HC^{2}$ + $\pi KB^{2}$
Stp = $\pi$.2a.6a - $\pi$.a.3a + $\pi$.$(2a)^{2}$ + $\pi a^{2}$ = 14$\pi a^{2}$