Chương II. MẶT CẦU, MẶT TRỤ, MẶT NÓN
§1. MẶT CẦU, KHỐI CẦU
A. KIẾN THỨC CẦN NHỚ
1. Định nghĩa
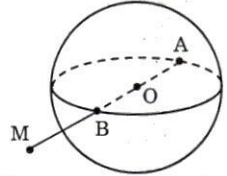
Tập các điểm trong không gian cách điểm O cố định một khoảng cách R cho trước gọi là mặt cầu có tâm là O và bán kính bằng R.
Kí hiệu: S(O; R).
Như vậy: S(O, R) = {M | OM = R},
a) Nếu trên mặt cầu S(O; R) ta lấy điểm A nào đó, thì đoạn thẳng OA cũng được gọi là bán kính của mặt cầu.
Nếu gọi B là điểm đối xứng của A qua điểm O thì điểm B nằm trên mặt cầu. Đoạn thẳng AB gọi là đường kính của mặt cầu.
b) Cho M là một điểm bất kì, ta có các trường hợp sau:
• Nếu OM = R thì điểm M nằm trên mặt cầu.
• Nếu OM > R thì ta nói rằng điểm M nằm ngoài mặt cầu.
• Nếu OM < R thì ta nói rằng điểm M nằm trong mặt cầu.
2. Vị trí tương đối giữa mặt cầu và mặt phẳng.
Cho mặt cầu S(O; R) và mặt phẳng (P). Gọi H là hình chiếu vuông góc của O trên mặt phẳng (P) và đặt d = OH (d là khoảng cách từ điểm O đến mặt phẳng (P). Khi đó:
• Nếu d< R thì mặt phẳng (P) cắt mặt cầu S(O; R) theo giao tuyến là đường tròn nằm trên mặt phẳng (P) có tâm là H và có bán kính là r = $\sqrt{R^{2}-d^{2}}$;
• Nếu d = R thì mặt phẳng (P) và mặt cầu S(O; R) chỉ có một điểm chung duy nhất là H, ta nói mặt phẳng (P) tiếp xúc với mặt cầu S(O; R) tại H, điểm H gọi là tiếp điểm và (P) gọi là tiếp diện của mặt cầu tại điểm H;
• Nếu d > R thì mặt phẳng (P) không cắt mặt cầu S(O; R).
Đặc biệt: Nếu d = 0 thì mặt phẳng (P) cắt mặt cầu S(O; R) theo một đường tròn (T) có tâm là O và có bán kính R. Đường tròn (T) gọi là đường tròn lớn của mặt cầu.
3. Vị trí tương đối giữa mặt cầu và đường thẳng
Cho mặt cầu S(O; R) và đường thẳng $\Delta$. Gọi H là hình chiếu vuông góc của O trên $\Delta$ và đặt d = OH (d là khoảng cách từ điểm O đến $\Delta$). Khi đó:
• Nếu d < R thì đường thẳng $\Delta$ cắt mặt cầu S(O; R) tại hai điểm phân biệt;
• Nếu d = R thì đường thẳng $\Delta$ và mặt cầu S(O; R) chỉ có một điểm chung duy nhất là H, ta nói đường thẳng $\Delta$ tiếp xúc với mặt cầu S(O; R) tại H, điểm H gọi là tiếp điểm và $\Delta$ gọi là tiếp tuyến của mặt cầu tại điểm H;
• Nếu d > R thì đường thẳng $\Delta$ không cắt mặt cầu S(O; R).
Định lí 1: Qua điểm A nằm trên mặt cầu S(O; R) có vô số tiếp tuyến của mặt cầu (S). Tất cả các tiếp tuyến này đều nằm trên tiếp diện của mặt cầu tại điểm A.
Định lí 2: Qua điểm A nằm ngoài mặt cầu S(O; R) có vô số tiếp tuyến của mặt cầu (S). Độ dài các đoạn thẳng kẻ từ A tới các tiếp điểm bằng nhau.
4. Mặt cầu ngoại tiếp một hình đa diện
.png)
Một mặt cầu đi qua mọi đỉnh của một hình đa diện H gọi là mặt cầu ngoại tiếp hình đa diện H, và hình đa diện H gọi là nội tiếp trong mặt cầu đó.
a) Bất kì hình tứ diện nào cũng có mặt cầu ngoại tiếp. Xét hình tứ diện ABCD. Gọi $\Delta$ là trục của đường tròn ngoại tiếp $\Delta$BCD và (P) là mặt trung trực của cạnh AB, thì tâm O của mặt cầu ngoại tiếp ABCD là giao điểm của $\Delta$ và (P).
b) Hình chóp $S.A_{1}A_{2}...A_{n}$ có mặt cầu ngoại tiếp khi và chỉ khi đáy $A_{1}A_{2}...A_{n}$ có đường tròn ngoại tiếp.
Tâm của mặt cầu ngoại tiếp hình chóp là giao điểm trục của đường tròn ngoại tiếp đa giác $A_{1}A_{2}...A_{n}$ và mặt trung trực một cạnh bên của hình chóp.
c) Hình lăng trụ $A_{1}A_{2}...A_{n}$. $A'_{1}A'_{2}...A'_{n}$ có mặt cầu ngoại tiếp khi và chỉ khi nó là hình lăng trụ đứng và đáy có đường tròn ngoại tiếp. Gọi I, I' lần lượt là tâm hai đáy (tâm đường tròn ngoại tiếp), thì tâm mặt cầu ngoại tiếp của hình lăng trụ là trung điểm O của đoạn thẳng II'.
5. Mặt cầu nội tiếp hình đa diện
Nếu có một mặt cầu (S) tiếp xúc với tất cả các mặt của một hình đa diện H thì ta nói (S) là mặt cầu nội tiếp trong hình đa diện H và H gọi là hình đa diện ngoại tiếp (S).
6. Diện tích mặt cầu và thể tích khối cầu
• Mặt cầu bán kính R có diện tích là: S = 4$\pi R^{2}$.
• Khối cầu bán kính R có thể tích là: V = $\large \frac{4}{3}$$R^{3}$.
