§2. PHƯƠNG TRÌNH CỦA MẶT PHẲNG
B/ CÂU HỎI VÀ BÀI TẬP
Bài 15. Viết phương trình mặt phẳng trong mỗi trường hợp sau:
a) Đi qua ba điểm M(2; 0; -1), N(1; -2; 3), P(0; 1; 2).
b) Đi qua hai điểm A(1; 1; -1), B(5; 2; 1) và song song với trục Oz.
c) Đi qua điểm (3; 2; -1) và song song với mặt phẳng có phương trình x – 5y + z = 0.
d) Đi qua hai điểm A(0; 1; 1), B(-1; 0; 2) và vuông góc với mặt phẳng x - y + z + 1 = 0.
e) Đi qua điểm M(a; b; c) (abc $\large \neq$ 0) và song song với một mặt phẳng tọa độ.
g) Đi qua điểm G(1; 2; 3) và cắt các trục tọa độ tại các điểm A, B, C sao cho G là trọng tâm tam giác ABC.
h) Đi qua điểm H(2; 1; 1) và cắt các trục tọa độ tại các điểm A, B, C sao cho H là trực tâm của tam giác ABC.
Giải
a) $\large \vec{MN}$ = (-1; -2; 4), $\large \vec{MP}$ = (-2; 1; 3)
Vectơ pháp tuyến của mp(MNP): [$\large \vec{MN}$, $\large \vec{MP}$] = (-10; -5 -5), cùng phương với $\large \vec{n}$ = (2; 1; 1).
Phương trình của mặt phẳng (MNP):
2.(x - 2) + 1.(y - 0) + 1.(z + 1) = 0 ⇔ 2x + y + z - 3 = 0
b) Gọi (P) là mặt phẳng cần tìm:
Ta có: $\large \vec{AB}$ = (4; 1; 2), $\large \vec{k}$ = (0; 0; 1)
Do (P) đi qua điểm A, B và song song với trục Oz nên có vectơ pháp tuyến là:
$\large \vec{n}$ = [$\large \vec{AB}$ , $\large \vec{k}$] = (1; -4; 0)
Phương trình của mặt phẳng (P):
1.(x - 1) - 4.(y - 1) = 0 ⇔ x - 4y + 3 = 0
c) Gọi (Q) là mặt phẳng cần tìm. Do (Q) song song với mặt phẳng x - 5y + z = 0 nên phương trình có dạng x – 5y + z + D = 0 (D $\large \neq$ 0)
Vì (Q) đi qua điểm (3; 2; -1) nên ta có D = 8
Vậy phương trình của (Q) là x – 5y + z + 8 = 0
d) $\large \vec{AB}$ = (-2; -1; 1), vectơ pháp tuyến của mặt phẳng x - y + z + 1 = 0 là $\large \vec{u}$ = (1; -1; 1)
Gọi (R) là mặt phẳng cần tìm, mặt phẳng (R) có vectơ pháp tuyến là:
[$\large \vec{AB}$, $\large \vec{u}$ ] = (0; 3; 3), cùng phương với vectơ $\large \vec{n}$ = (0; 1; 1).
Phương trình của mp(R):
1.(y - 1) + 1.(z - 1) = 0 ⇔ y + z - 2 = 0
e) * Mặt phẳng đi qua điểm M(a; b; c) và song song với mp(Oxy) có phương trình z = c.
* Mặt phẳng đi qua điểm M(a; b; c) và song song với mp(Oyz) có phương trình x = a.
* Mặt phẳng đi qua điểm M(a; b; c) và song song với mp(Oxz) có phương trình y = b.
g) Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c). Vì G(1; 2; 3) là trọng tâm của $\Delta$ABC nên ta có:
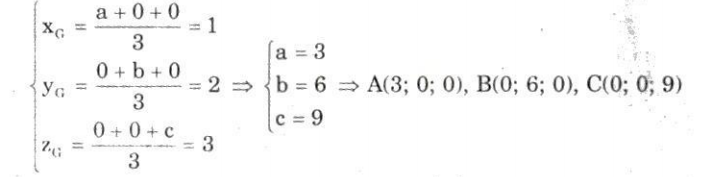
Phương trình của mặt phẳng cần tìm là:
$\large \frac{x}{3}$ + $\large \frac{y}{6}$ + $\large \frac{z}{9}$ = 1 ⇔ 6x + 3y + 2z - 18 = 0
h)
.png)
Gọi ($\large \alpha$) là mặt phẳng cần tìm. Trước hết ta chứng minh rằng OH $\large \perp$ mp($\large \alpha$). Kéo dài CH cắt AB tại điểm I. Do H là trực tâm của $\Delta$ABC nên CI $\perp$ AB. Từ giả thiết ta có:
OC $\perp$ (OAB) ⇒ OC $\perp$ AB
Suy ra AB $\perp$ (OCI) ⇒ AB $\perp$ OH
Chứng minh tương tự ta được BC $\perp$ OH
Do vậy: OH $\perp$ (ABC) hay OH $\perp$ mp($\alpha$).
Tóm lại, từ giả thiết ta suy ra được ($\alpha$) là mặt phẳng vuông góc với OH tại điểm H.
Một vectơ pháp tuyến của ($\alpha$) là: $\vec{n}$ = $\vec{OH}$ = (2; 1; 1)
Phương trình của mp($\alpha$) là:
2(x - 2) + 1(y - 1) + 1(z-1) = 0 ⇔ 2x + y + z - 6 = 0.
Bài 16. Xét vị trí tương đối của mỗi cặp mặt phẳng cho bởi các phương trình sau:
a) x + 2y - z + 5 = 0 và 2x + 3y – 7z – 4 = 0
b) x - 2y + z - 3 = 0 và 2x - y + 4z - 2 = 0
c) x + y + z - 1 = 0 và 2x + 2y + 2z + 3 = 0
d) 3x - 2y + 3z + 5 = 0 và 9x - 6y - 9z - 5 = 0
e) x - y + 2z - 4 = 0 và 10x – 10y + 20z - 40 = 0.
Giải
a) Gọi ($\alpha$): x + 2y - z + 5 = 0, ($\beta$): 2x + 3y - 7z - 4 = 0
Do 1 : 2 : (-1) $\neq$ 2 : 3 : (-7) nên hai mặt phẳng ($\alpha$) và ($\beta$) cắt nhau.
b) Gọi ($\alpha$): x - 2y + z – 3 = 0, ($\beta$): 2x - y + 4z – 2 = 0
Do: 1 : (-2) : 1 $\neq$ 2 : (-1) : 4 nên hai mặt phẳng ($\alpha$) và ($\beta$) cắt nhau.
c) Gọi ($\alpha$): x + y + z - 1 = 0, ($\beta$): 2x + 2y + 2z + 3 = 0
Do $\large \frac{1}{2}$ = $\large \frac{1}{2}$ = $\large \frac{1}{2}$ $\neq$ $\large \frac{-1}{3}$ nên ($\alpha$) // ($\beta$)
d) Gọi ($\alpha$): 3x - 2y + 3z + 5 = 0, ($\beta$): 9x - 6y - 9z – 5 = 0
Do 3 : (-2) : 3 $\neq$ 9 : (-6) : (-9) nên hai mặt phẳng ($\alpha$) và ($\beta$) cắt nhau.
e) Gọi ($\alpha$): x - y + 2z - 4 = 0, ($\beta$): 10x - 10y + 20z - 40 = 0
Do $\large \frac{1}{10}$ = $\large \frac{-1}{-10}$ = $\large \frac{2}{20}$ = $\large \frac{-4}{-40}$ nên ($\alpha$) $\equiv$ ($\beta$)
Bài 17. Xác định giá trị của m và n để mỗi cặp mặt phẳng sau đây song song:
a) 2x + ny + 2z + 3 = 0 và mx + 2y - 4z + 7 = 0.
b) 2x + y + mz - 2 = 0 và x + ny + 2z + 8 = 0.
Giải
a) Điều kiện để hai mặt phẳng đã cho song song với nhau là:
.png)
Vậy khi m = -4 và n = -1 thì hai mặt phẳng đã cho song song với nhau.
b) Điều kiện để hai mặt phẳng đã cho song song với nhau là:
.png)
Vậy khi m = 4 và n = $\large \frac{1}{2}$ thì hai mặt phẳng đã cho song song với nhau.
Bài 18. Cho hai mặt phẳng có phương trình lần lượt là:
2x - my + 3z - 6 + m = 0 và (m + 3)x - 2y + (5m + 1)z – 10 = 0
Với giá trị nào của m thì:
a) Hai mặt phẳng đó song song?
b) Hai mặt phẳng đó trùng nhau?
c) Hai mặt phẳng đó cắt nhau?
d) Hai mặt phẳng đó vuông góc?
Giải
Gọi ($\alpha$): 2x – my + 3z – 6 + m = 0, ($\beta$): (m + 3)x - 2y + (5m + 1)z – 10 = 0
a) Hai mặt phẳng ($\alpha$) và ($\beta$) song song với nhau khi và chỉ khi:
.png)
Nhận thấy m = 1 không nghiệm đúng (*).
Vậy không có giá trị nào của m để ($\alpha$) và ($\beta$) song song với nhau.
b) Hai mặt phẳng ($\alpha$) và ($\beta$) trùng nhau khi và chỉ khi:
.png)
Vậy nếu m = 1 thì hai mặt phẳng ($\alpha$) và ($\beta$) trùng nhau.
c) Hai mặt phẳng ($\alpha$) và ($\beta$) cắt nhau khi và chỉ khi:
.png)
Vậy nếu m $\neq$ 1 thì hai mặt phẳng ($\alpha$) và ($\beta$) cắt nhau.
Ghi chú: Có thể suy từ kết quả hai câu a) và b)
d) Hai mặt phẳng ($\alpha$) và ($\beta$) vuông góc với nhau khi và chỉ khi:
2(m + 3) + (-m).(-2) + 3.(5m + 1) = 0 ⇔ m = $\large \frac{-9}{19}$
Bài 19. Tìm tập hợp các điểm cách đều hai mặt phẳng ($\alpha$) và ($\alpha$') trong mỗi trường hợp sau:
a) ($\alpha$): 2x - y + 4z + 5 = 0, ($\alpha$'): 3x + 5y - z - 1 = 0;
b) ($\alpha$): 2x + y – 2z - 1 = 0, ($\alpha$'): 6x – 3y + 2z - 2 = 0;
c) ($\alpha$): x + 2y + z - 1 = 0, ($\alpha$'): x + 2y + z + 5 = 0.
Giải
Gọi M(x; y; z) là điểm cách đều ($\alpha$) và ($\alpha$') ta có:
a) d(M, ($\alpha$)) = d(M, ($\alpha$')) ⇔ $\large \frac{\mid 2x-y+4z+5\mid }{\sqrt{21}}$ = $\large \frac{\mid 3x+5y-z-1\mid }{\sqrt{35}}$
⇔ $\sqrt{5}$$\mid$ 2x - y + 4z + 5$\mid$ = $\sqrt{3}$$\mid$ 3x + 5y - z - 1$\mid$
⇔ .png)
Vậy tập hợp các điểm M gồm hai mặt phẳng có phương trình định bởi (1) và (2).
b) d(M, ($\alpha$)) = d(M, ($\alpha$')) ⇔ $\large \frac{\mid 2x+y-2z-1\mid }{3}$ = $\large \frac{\mid 6x-3y+2z-2\mid }{7}$
⇔ 7$\mid$ 2x + y - 2z - 1$\mid$ = 3$\mid$ 6x - 3y + 2z - 2$\mid$
⇔ .png)
Vậy tập hợp các điểm M gồm hai mặt phẳng có phương trình định bởi (1) và (2).
c) d(M, ($\alpha$)) = d(M, ($\alpha$')) ⇔ $\large \frac{\mid x+2y+z-1\mid }{\sqrt{6}}$ = $\large \frac{\mid x+2y+z+5\mid }{\sqrt{6}}$
.png)
⇔ x + 2y + z + 2 = 0
Vậy tập hợp các điểm M là một mặt phẳng có phương trình x + 2y + z + 2 = 0.
Bài 20. Tìm khoảng cách giữa hai mặt phẳng Ax + By + Cz + D = 0 và Ax + By + Cz + D' = 0 với D $\neq$ D'
Giải
Gọi ($\alpha$), ($\beta$) lần lượt là hai mặt phẳng có phương trình đã cho. Hiển nhiên hai mặt phẳng đã cho là song song với nhau.
Lấy điểm $M_{0}$($x_{0}$; $y_{0}$; $z_{0}$) $\in$ ($\alpha$) tức là A$x_{0}$ + B$y_{0}$ + C$z_{0}$ + D = 0.
Ta có: d(($\alpha$), ($\beta$)) = d($M_{0}$, ($\beta$)) = $\large \frac{\mid Ax_{0}+By_{0}+Cz_{0}+D'\mid }{\sqrt{A^{2}+B^{2}+C^{2}}}$
= $\large \frac{\mid -D+D'\mid }{\sqrt{A^{2}+B^{2}+C^{2}}}$ = $\large \frac{\mid D-D'\mid }{\sqrt{A^{2}+B^{2}+C^{2}}}$
Bài 21. Tìm điểm M trên trục Oz trong mỗi trường hợp sau:
a) M cách đều điểm A(2; 3; 4) và mặt phẳng 2x + 3y + z - 17 = 0;
b) M cách đều hai mặt phẳng x + y - z + 1 = 0 và x - y + z + 5 = 0.
Giải
a) Lấy điểm M(0; 0; z) $\in$ Oz. Điểm M cách đều điểm A và mặt phẳng ($\alpha$) khi và chỉ khi:
d(M, ($\alpha$)) = AM ⇔ $\large \frac{\mid 2.0+3.0+z-17\mid }{\sqrt{2^{2}+3^{2}+1^{2}}}$ = $\sqrt{(0-2)^{2}+(0-3)^{2}+(z-4)^{2}}$
⇔ $\mid z-17\mid$ = $\sqrt{14}$.$\sqrt{z^{2}-8z+29}$
Bình phương hai vế và thu gọn ta được:
$z^{2}$ - 6z + 9 = 0 ⇔ $(z-3)^{2}$ = 0 ⇔ z = 3.
Vậy M(0; 0; 3).
b) Lấy điểm M(0; 0; z) $\in$ Oz. Điểm M cách đều hai mặt phẳng ($\alpha$) và ($\beta$) khi và chỉ khi:
d (M, ($\alpha$)) = d(M, ($\beta$)) = $\large \frac{\mid 0+0-z+1\mid }{\sqrt{3}}$ = $\large \frac{\mid 0-0+z+5\mid }{\sqrt{3}}$
⇔ $\mid 1-z\mid$ = $\mid z+5\mid$ ⇔ .png) ⇔ z = -2
⇔ z = -2
Vậy M(0; 0; -2).
Bài 22. Cho tứ diện OABC có các tam giác OAB, OBC, OCA là những tam giác vuông đỉnh O. Gọi $\alpha$, $\beta$, $\gamma$ lần lượt là góc giữa mặt phẳng (ABC) và các mặt phẳng (OBC), (OCA), (OAB). Bằng phương pháp tọa độ, hãy chứng minh:
a) Tam giác ABC có ba góc nhọn;
b) $cos^{2}\alpha$ + $cos^{2}\beta$ + $cos^{2}\gamma$ = 1.
Giải
.png)
Đặt OA = a, OB = b, OC = c.
Chọn hệ Oxyz sao cho O là gốc tọa độ, A(a; 0; 0), B(0; b; 0), C(0; 0; c).
a) $\vec{AB}$ = (-a; b; 0), $\vec{AC}$ = (-a; 0; c)
Ta có: cosA = cos($\vec{AB}$, $\vec{AC}$) = $\large \frac{a^{2}}{\sqrt{a^{2}+b^{2}}.\sqrt{a^{2}+c^{2}}}$ > 0
Do đó góc $\widehat{A}$ của $\Delta$ABC là một góc nhọn.
Chứng minh tương tự các góc $\widehat{B}$ và $\widehat{C}$ cũng là các góc nhọn.
b) Mặt phẳng (OAB) tức mp(Oxy) có vectơ pháp tuyến $\vec{k}$ = (0; 0; 1)
Mặt phẳng (ABC) có vectơ pháp tuyến $\vec{n}$ = [$\vec{AB}$,$\vec{AC}$] = (bc; ac; ab)
.png)
Vậy: $cos^{2}\alpha$ + $cos^{2}\beta$ + $cos^{2}\gamma$ = 1.
Bài 23. Viết phương trình mặt phẳng song song với mặt phẳng 4x + 3y - 12z + 1 = 0 và tiếp xúc với mặt cầu có phương trình:
$x^{2}$ + $y^{2}$ + $z^{2}$ - 2x - 4y - 6z - 2 = 0
Giải
Phương trình của mặt cầu viết lại:
$(x-1)^{2}$ + $(y-2)^{2}$ + $(z-3)^{2}$ = 16 (S)
Suy ra (S) có tâm I(1; 2; 3), bán kính R = 4
Phương trình của mặt phẳng (P) song song với mặt phẳng 4x + 3y - 12x + 1 = 0 có dạng: 4x + 3y - 12x + D = 0
Mặt phẳng (P) tiếp xúc với (S) khi và chỉ khi:
d(I, (P)) =R ⇔ $\large \frac{\mid -24+D\mid }{13}$ = 4 ⇔ $\mid$-26 + D$\mid$ = 52 ⇔ .png)
Vậy phương trình của mặt phẳng cần tìm là:
4x + 3y - 12z + 78 = 0 hoặc 4x + 3y - 12z – 26 = 0
