Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
A. KIẾN THỨC, VÍ DỤ VÀ BÀI TẬP CĂN BẢN
§1. CÁC HÀM SỐ LƯỢNG GIÁC
1.1. Các hàm số y = sinx và y = cosx
• Hàm số y = sinx:
a) Có tập xác định là R;
b) Là một hàm số lẻ, đồ thị nhận gốc tọa độ làm tâm đối xứng;
c) Tuần hoàn với chu kì 2$\pi$;
d) Đồng biến trên mỗi khoảng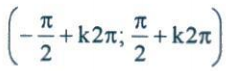 
và nghịch biến trên mỗi khoảng .png)
với k $\in$ Z;
e) Có tập giá trị là I = [-1, 1];
f) Có đồ thị là một đường hình sin.
• Hàm số y = cosx:
a) Có tập xác định là R;
b) Là một hàm số chẵn, đồ thị nhận trục tung làm trục đối xứng;
c) Tuần hoàn với chu kì 2$\pi$;
d) Đồng biến trên mỗi khoảng ((2k -1)$\pi$; k2$\pi$) và nghịch biến trên mỗi khoảng (2k$\pi$; (2k + 1)$\pi$), với k $\in$ Z;
e) Có tập giá trị là I = [-1, 1];
f) Có đồ thị là một đường hình sin.
Chú ý. Số dương L nhỏ nhất thỏa mãn f(x + L) = f(x) (với mọi x thuộc miền xác định của hàm f(x)) được gọi là chu kì của hàm số f(x).
Ví dụ 1.
Tìm miền giá trị của hàm số y = $sin^{6}$x + $cos^{6}$x.
Giải.
Trước tiên, ta có biến đổi như sau:
.png)
Miền giá trị của hàm số y = sin2x là I = [-1, 1]. Suy ra miền giá trị của hàm số y = $sin^{2}$2x là [0, 1].
.png)
Từ đó, miền giá trị của hàm số .png)
Ví dụ 2
Cho hàm số f(x) = sin2x + cos3x. Chứng minh rằng
f(x) = f(x + k2$\pi$), với mọi k $\in$ Z, mọi x $\in$ R.
Giải.
Ta có sin 2x = sin(2x + k2$\pi$) = sin 2(x + k$\pi$). Tương tự,
.png)
Vì đẳng thức sin 2x = sin 2(x + k$\pi$) đúng cho mọi số nguyên k nên:
sin 2x = sin 2(x + 2k$\pi$) = sin 2(x + k2$\pi$).
Ta cũng có .png)
Vì đẳng thức .png)
đúng cho mọi số nguyên k nên :
.png)
Từ đó ta có
f(x) = sin 2x + cos 3x = sin 2(x + k2$\pi$) + cos3(x + k2$\pi$) = f(x + k2$\pi$) với mọi k $\in$ Z, mọi x $\in$ R.
Cách khác : Ta có
f(x + k2$\pi$) = sin 2(x + k2$\pi$) + cos3(x + k2$\pi$)
= sin(2x + k4$\pi$)+ cos(3x + k6$\pi$)
= sin(2x + 2k2$\pi$) + cos(3x + 3k2$\pi$)
= sin 2x + cos3x = f(x).
Ví dụ 3. Tìm giá trị nhỏ nhất của hàm số y = sin$\large \frac{A}{2}$ - $\sqrt{3}$cos$\large \frac{A}{2}$
Giải.
.png)
Vậy giá trị nhỏ nhất của T là -2, giá trị này đạt được tại nhiều giá trị, chẳng hạn, khi
$\large \frac{A}{2}$ - 60° = -90° ⇔ A = -60°
1.1. Các hàm số y = tanx và y = cotx
• Hàm số y = tan x:
a) Có tập xác định là .png)
b) Là một hàm số lẻ ;
c) Tuần hoàn với chu kì $\pi$;
d) Đồng biến trên mỗi khoảng .png)
với k $\in$ Z;
e) Có tập giá trị là R;
f) Có đồ thị nhận các đường thẳng .png)
với k $\in$ Z, làm các tiệm cận đứng.
• Hàm số y = cotx:
a) Có tập xác định là R \ {k$\pi$ | k $\in$ Z} ;
b) Là một hàm số lẻ ;
c) Tuần hoàn với chu kì $\pi$ ;
d) Nghịch biến trên mỗi khoảng (k$\pi$ ; (k + 1)$\pi$), với k $\in$ Z;
e) Có tập giá trị là R;
f) Có đồ thị nhận các đường thẳng x = k$\pi$, với k $\in$ Z, làm các tiệm cận đứng.
Ví dụ 4. Xét tính chẵn lẻ của các hàm số :
a) y = sinx$cos^{2}$x + tan x;
b) y = tan x - sin 2x.
Giải.
a) Đặt f(x) = sinx$cos^{2}$x + tan x, ta có
f(-x) = sin(-x)$cos^{2}$(-x) + tan(-x)
= -sinx$cos^{2}$x - tan x = -f(x).
Vậy f(x) = sinx$cos^{2}$x + tan x là hàm số lẻ.
b) f(-x) = tan(-x) - sin(-2x) = -tanx + sin2x = -f(x).
Vậy y = tan x - sin2x là hàm số lẻ.
Ví dụ 5.
Để “chứng minh” hàm số y = $tan^{2}$x có chu kì là $\large \frac{\pi }{2}$, một học sinh tiến hành như sau:
Giải. Với mọi x thuộc miền xác định, ta có
.png)
Vì tan x và tan(x + $\large \frac{\pi }{2}$) trái dấu nhau nên ta có đẳng thức trên.
Vậy chu kì của hàm số y = $tan^{2}$x là $\large \frac{\pi }{2}$:
Em hãy cho nhận xét về lời giải trên.
Nhận xét về bài giải. Trước hết, học sinh đó đã sai lầm ở chỗ : Nếu x = 0 (thuộc miền xác định của hàm số y = $tan^{2}$x) thì giá trị (0 + $\large \frac{\pi }{2}$) lại không thuộc miền xác định của hàm số đó.
Ngoài ra, để chứng minh một số L là chu kì của một hàm số, ta còn phải chứng minh thêm rằng L là số dương nhỏ nhất thỏa mãn f(x + L) = f(x) (với mọi x thuộc miền xác định của hàm f(x)).
Ví dụ 6.
Biết sinx + cosx = $\large \frac{1}{5}$ và 0 $\leq$ x $\leq$ $\pi$, hãy tính tan x.
Giải
.png)
Giải phương trình này ta được: y = $\large \frac{4}{5}$ hay y = -$\large \frac{3}{5}$
Giá trị -$\large \frac{3}{5}$ không chấp nhận được do giả thiết 0 $\leq$ x < $\pi$ .
Vậy sinx = $\large \frac{4}{5}$, suy ra : cosx = $\large \frac{1}{5}$ - sinx = -$\large \frac{3}{5}$, và:
.png)
BÀI TẬP
1.1. Có thể kết luận rằng chu kì của hàm số y = $sin^{2}$x là 2$\pi$ được không?
1.2. Có thể kết luận rằng chu kì của hàm số y = $cos^{2}$x là 2$\pi$ được không?
1.3. Cho tam giác vuông ABC, gọi D, E là hai điểm trên cạnh huyền BC sao cho BD = DE = EC. Biết độ dài các đoạn thẳng:
AD = sinx, AE = cosx với 0 < x < $\large \frac{\pi }{2}$
Tính độ dài cạnh huyền BC.
HƯỚNG DẪN GIẢI
1.1. Không thể kết luận như thế. Thật vậy, ta có:
$sin^{2}$x = sin x.sin x = sin(x + $\pi$).sin(x + $\pi$) = $sin^{2}$(x + $\pi$).
(Để ý rằng sinx và sin(x + $\pi$) cùng bằng 0 hoặc trái dấu nhau).
Vậy ta có f(x) = $sin^{2}$ x = $sin^{2}$(x + $\pi$) = f(x + $\pi$) với mọi x $\in$ R. Dĩ nhiên, f(x) = f(x + 2$\pi$), với mọi x thuộc R. Tuy nhiên, số 2$\pi$ không còn là số dương L nhỏ nhất thỏa mãn f(x) = f(x + L) được nữa (với mọi x thuộc R).
1.2. Ta có
$cos^{2}$x = cosx.cosx = cos(x + $\pi$).cos(x + $\pi$) = $cos^{2}$(x + $\pi$).
Lí luận tương tự như bài trên, không thể kết luận như thế.
1.3. Từ D, E vẽ lần lượt các đoạn DF, EG vuông góc với AC, cho ta:
CF = FG = GA = b và DF = 2EG = 2a. Áp dụng định lí Pi-ta-go vào các tam giác CDF và CEG, ta được :
4$a^{2}$ + $b^{2}$ = $sin^{2}$x,
$a^{2}$ + 4$b^{2}$ = $cos^{2}$x.
Cộng hai phương trình này ta suy ra: 5($a^{2}$ + $b^{2}$) = 1. Do đó:
.png)