§3. ĐẠO HÀM CỦA CÁC HÀM SỐ LƯỢNG GIÁC
3.1. Định lí về giới hạn
.png)
Chúng ta đã được giới thiệu giới hạn trên và các bài toán khó áp dụng giới hạn này trong phần mở rộng (mục 2, trang 146). Kết quả cần nhớ suy từ giới hạn trên là
.png)
Định lí trên là cơ sở để chứng minh các công thức về đạo hàm của hàm lượng giác như trong 3.2 dưới đây.
3.2. Đạo hàm của các hàm số lượng giác
3.2.1. Đạo hàm của hàm số y = sinx
Hàm số y = sinx có đạo hàm tại mọi x $\in$ R và (sinx)' = cosx.
3.2.2. Đạo hàm của hàm số y = cosx
Hàm số y = cosx có đạo hàm tại mọi x $\in$ R, và (cosx)' = -sinx.
3.2.3. Đạo hàm của hàm số y = tanx
Hàm số y = tanx có đạo hàm tại mọi .png)
.png)
3.2.4. Đạo hàm của hàm số y = cotx
Hàm số y = cotx có đạo hàm tại mọi .png)
và
.png)
BẢNG TÓM TẮT CÁC ĐẠO HÀM ĐÃ HỌC
.png)
Ví dụ 13.
Tính đạo hàm của các hàm số
.png)
Giải.
.png)
.png)
Ví dụ 14. (Trích đề thi vào ĐH Huế, khối A, B, năm 2000)
Cho hàm số f xác định bởi
.png)
a) Tính đạo hàm của f tại mỗi x $\in$ R.
b) Chứng minh rằng đạo hàm f' là hàm số không liên tục tại điểm x = 0.
Giải.
.png)
b) Theo trên, ta có
.png)
Mặt khác, .png)
lại không có giới hạn nên f'(x) cũng không có giới hạn khi x → 0. Thật vậy, nếu không như thế, nghĩa là f'(x) → a khi x → 0 thì .png)
cũng có giới hạn là a khi x → 0, điều này vô lí.
Vậy f'(x) không liên tục tại điểm x = 0.
Ví dụ 15. Chứng minh rằng hàm số sau đây có đạo hàm không phụ thuộc vào x:
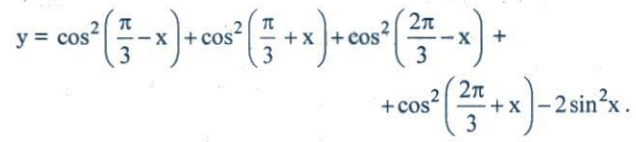
Giải.
.png)
Cách 2. Áp dụng công thức hạ bậc, ta được :
.png)
Vậy y' = 0. Do đó y' không phụ thuộc x.
BÀI TẬP
5.7. Cho f(x) = 2$x^{2}$ - x + 2 và g(x) = f(sinx). Tính g'(x)?
5.8.
Tính đạo hàm của các hàm số
.png)
5.9. Tính .png)
biết rằng f(x) = $x^{2}$ và .png)
5.10. Chứng minh rằng hàm số sau đây có đạo hàm không phụ thuộc vào x:
y = $sin^{6}$x + $cos^{6}$x + 3$sin^{2}$x$cos^{2}$x
HƯỚNG DẪN GIẢI
5.7.
g'(x) = 2sin2x + cosx.
5.8.
.png)
5.9. .png)
5.10. Cách 1. Ta có :
.png)
Cách 2. Ta có:
.png)
Do đó y' không phụ thuộc x.