B. MỘT SỐ KIẾN THỨC VÀ VÍ DỤ MỞ RỘNG

§1. CÁC VÍ DỤ NÂNG CAO VỀ GIỚI HẠN CỦA DÃY SỐ

Các ví dụ sau đây cho thấy rõ hơn về tầm quan trọng của định lí kẹp trong lí thuyết giới hạn (dãy hoặc hàm số).

Ví dụ 27.

Chứng minh rằng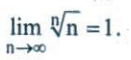

Giải.

Trước tiên, ta có $\sqrt[n]{n}\geq 1$ với mọi số tự nhiên n. Thật vậy, nếu xảy ra điều ngược lại, thì $\sqrt[n]{n}$ < 1 ⇔ n < $1^{n}$, là điều vô lí.

Tiếp theo, áp dụng bất đẳng thức Côsi có:

Vậy ta đã chứng minh được rằng

Từ đây, do nên ta suy ra điều phải chứng minh.

Ví dụ 28.

Tính

Giải.

Để ý rằng Do đó với n $\geq$ 4 ta có

Ví dụ 29.

Cho hai dãy ($u_{n}$) và ($v_{n}$) có số hạng tổng quát là

a) Chứng minh rằng ($u_{n}$) là dãy đơn điệu tăng.

b) Chứng minh rằng ($v_{n}$) là dãy đơn điệu giảm.

c) Tính

Giải.

Đây chính là bất đẳng thức Bernoulli dạng đơn giản. Các bạn có thể sử dụng quy nạp để chứng minh bất đẳng thức này. Sử dụng (2) và để ý rằng ta được

Kết hợp (1) và (3) ta có

Như vậy với mọi n $\in$ N.

Do đó ($u_{n}$) là dãy đơn điệu tăng.

Chú ý: Ta có giải bằng cách khác như sau:

Áp bất đẳng thức Côsi cho n + 1 số:

b) Ta có

(Bất đẳng thức trên xảy ra do ta đã áp dụng (2)).

Như vậy

Nói cách khác, ($v_{n}$) là dãy đơn điệu giảm.

c) Ta sẽ dùng định lí kẹp để chứng minh rằng

Trước tiên, ta có:

suy ra rằng $v_{n}$ > $u_{n}$ với mọi số tự nhiên n.

Bây giờ, áp dụng điều này và tính chất tăng, giảm tương ứng của hai dãy ($u_{n}$), ($v_{n}$) như đã chứng minh trên, ta có

Sau cùng, vì nên theo định lí kẹp, suy ra điều phải chứng minh.